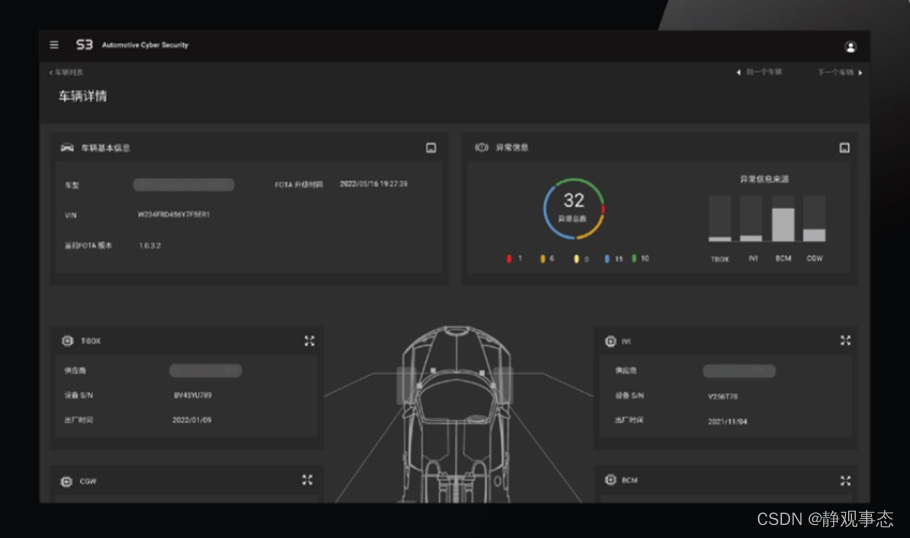
摘要: 卷积操作保留体现了空间相关性.
1. 卷积操作
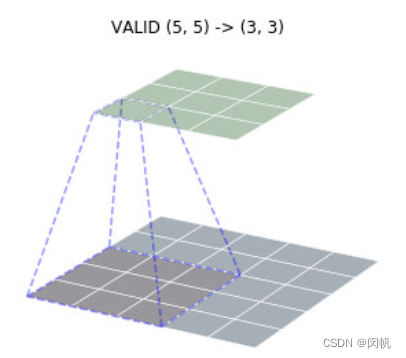
图 1 下平面标定的
3
×
3
3 \times 3
3×3 区域, 对应于个
3
×
3
3 \times 3
3×3 卷积, 这
9
9
9 个数对应着相乘, 然后相加, 获得了上平面标定的
1
1
1 个小区域的值. 注意这里不是矩阵的乘法.
卷积有三种方模式, 可以把图片变大 (full)、变小 (valid)、保持尺寸 (same).
与全连接网络相同, 卷积神经网络 CNN 也需要在加权和之后使用激活函数, 以使其具有非线性的优点.
2. 池化操作
100
×
100
100 \times 100
100×100 的图片, 用
3
×
3
3 \times 3
3×3 卷积核去卷, 第 2 层变成
98
×
98
98 \times 98
98×98 图片, 第 3 层变成
96
×
96
96 \times 96
96×96 图片, 太慢啦! 用池化操作可以把多个点压缩成一个点, 如把
98
×
98
98 \times 98
98×98 图片每
2
×
2
2 \times 2
2×2 个点取最大值 (或平均值, 最小值), 瞬间变成
49
×
49
49 \times 49
49×49 的图片.
是不是很随意的样子? 有效就行.
3. 卷积的优势
- 共享权值.
全连接网络的每个权值均只服务于一对节点. 也就是说, 如果第 i i i 层节点有 2 8 = 256 2^8 = 256 28=256 个, 第 i + 1 i + 1 i+1 层节点有 2 7 = 128 2^7 = 128 27=128 个, 则这两层节点之间的权值就有 2 8 × 2 7 = 2 1 5 = 32 , 768 2^8 \times 2^7 = 2^15 = 32,768 28×27=215=32,768 个. 如果有 10 10 10 层, 就几乎是 327 , 680 327,680 327,680 个. 对于 100 × 100 100 \times 100 100×100 的图片, 输入层就有 10 , 000 10,000 10,000 个节点, 更是难于计算. 但使用卷积后, 这 9 9 9 个权值被整张图共享受, 即使图片的深度为 100 100 100 (也就是一张图片用 100 100 100 卷积核分别进行特征提取, 生成 100 100 100 张新图片), 该层涉及的权值也只有 900 900 900 个. 共享权值还保证用同一个方式看图片的不同区域. - 感受野.
每个新的特征 (即图 1 上平面的每个点), 都来自于上一层局部特征. 这样保证空间上相邻的数据才被一起处理. 而全连接无法体现空间相邻性, 因为每个特征都是独立的. 这也是 CNN 对图片有效的主要原因.