---

打家劫舍

力扣连接：198. 打家劫舍（中等）

1.方法

1. 确定dp数组（dp table）以及下标的含义
   dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。

图解步骤

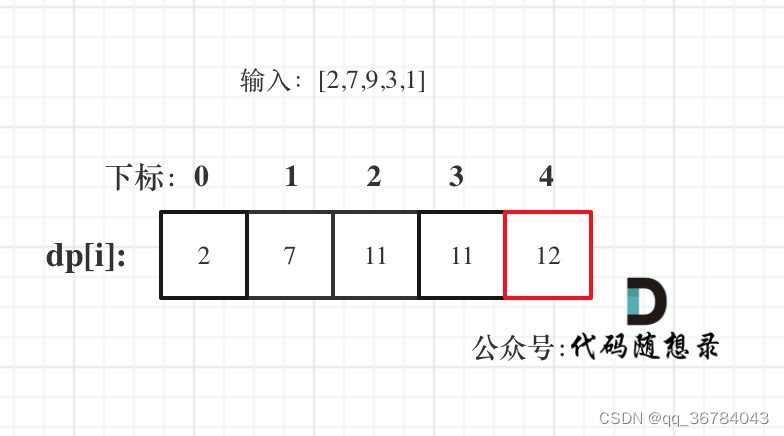
关键点：

• 如果不偷第i房间，那么dp[i] = dp[i - 1]，即考 虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）

代码

class Solution {
    public int rob(int[] nums) {
        int len = nums.length;
        if(len==1) return nums[0];

        int[] dp = new int[len];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0], nums[1]);
        for(int i=2;i<nums.length;i++){
            dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
        }

        return dp[len-1];
    }
}

---

---

打家劫舍 II

力扣连接：213. 打家劫舍 II（中等）

1.方法

对于一个数组，成环的话主要有如下三种情况：

情况一：考虑不包含首尾元素

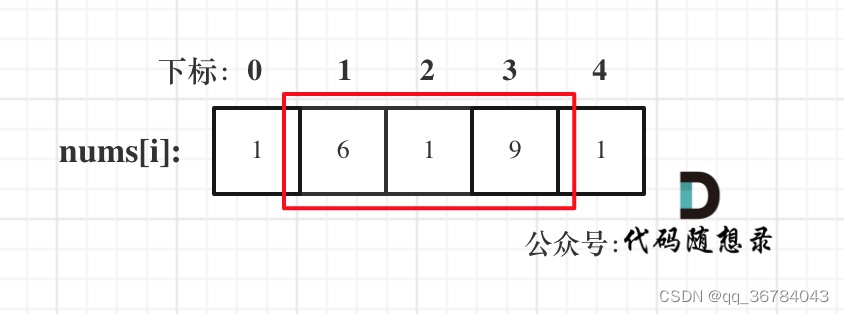
情况二：考虑包含首元素，不包含尾元素

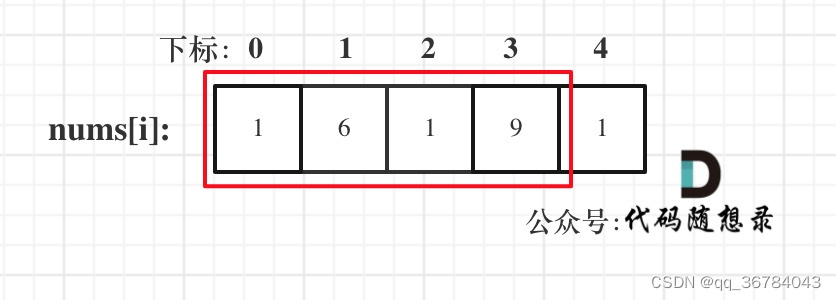
情况三：考虑包含尾元素，不包含首元素

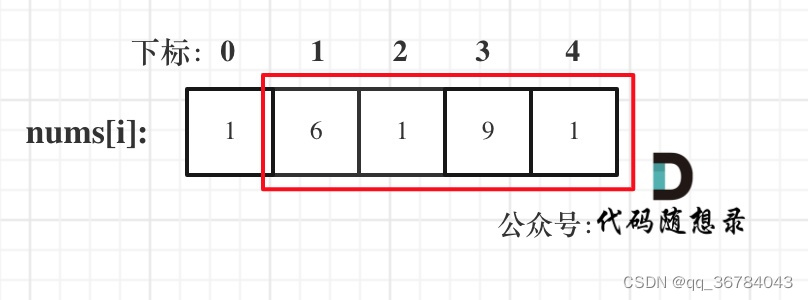
注意我这里用的是"考虑"，例如情况三，虽然是考虑包含尾元素，但不一定要选尾部元素！ 对于情况三，取nums[1] 和 nums[3]就是最大的。

而情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了。

代码

class Solution {
    public int rob(int[] nums) {
        int len = nums.length;
        if(len==1) return nums[0];
        if(len==2) return Math.max(nums[0], nums[1]);

        int result1 = robRange(nums, 0, len-2);
        int result2 = robRange(nums, 1, len-1);

        return Math.max(result1, result2);
    }

    public int robRange(int[] nums, int start, int end){
        int len = nums.length;
        int[] dp = new int[len];
        dp[start] = nums[start];
        dp[start+1] = Math.max(nums[start], nums[start + 1]);
        for(int i= start + 2; i<=end;i++){
            dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
        }

        return dp[end];
    }
}

---

---

打家劫舍 III

力扣连接：337. 打家劫舍 III（中等）

1. dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。
   所以本题dp数组就是一个长度为2的数组！
   因为在递归的过程中，系统栈会保存每一层递归的参数。

图解步骤

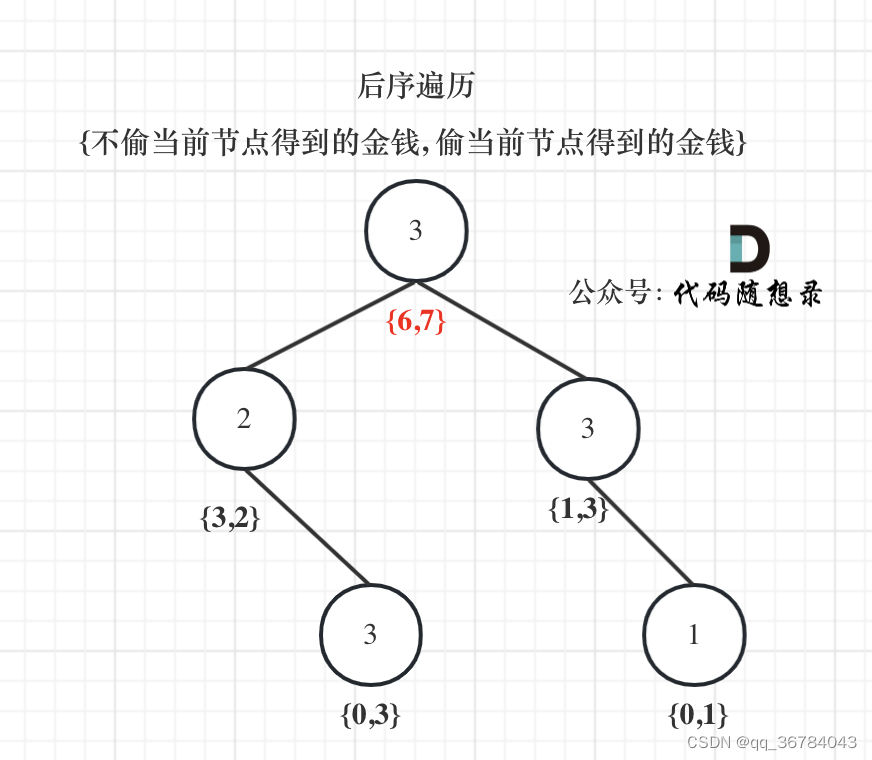
关键点：

• 如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以：val0 = max(left[0], left[1]) + max(right[0], right[1]);

代码

class Solution {
    public int rob(TreeNode root) {
        int[] result = robTree(root);

        return Math.max(result[0], result[1]);
    }

    public int[] robTree(TreeNode cur){
        if(cur==null) return new int[]{0, 0};

        //后续遍历，左右中
        int[] left = robTree(cur.left);
        int[] right = robTree(cur.right);

        int val0 = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        int val1 = cur.val + left[0] + right[0];
        
        return new int[]{val0, val1};
    }
}

---

---