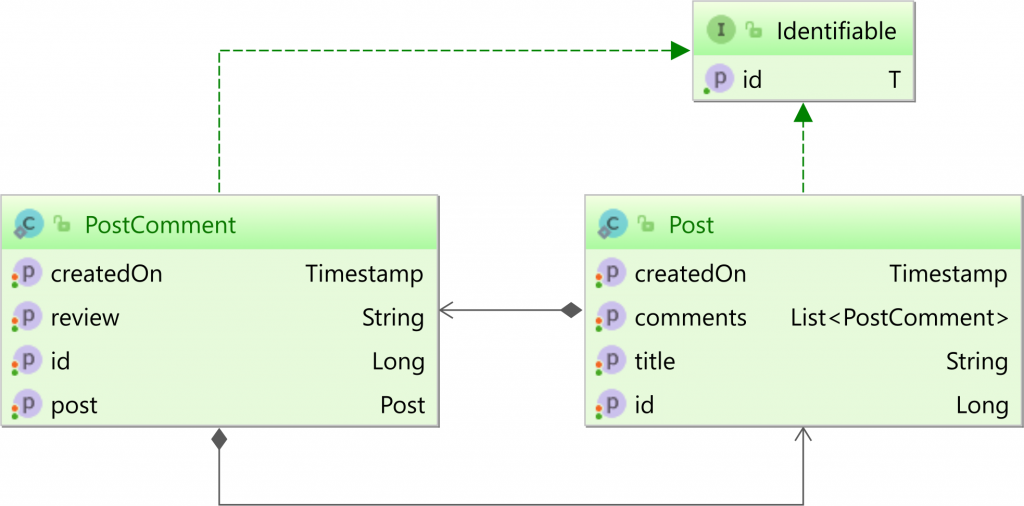
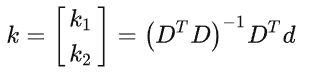摄像机标定

齐次坐标

齐次坐标，将欧氏空间的无穷远点，与投影空间中有实际意义的消失点，建立起映射关系。

把齐次坐标转化为笛卡尔坐标的方法：是前面n-1个坐标分量分别除以最后一个分量即可

一些解释和性质：

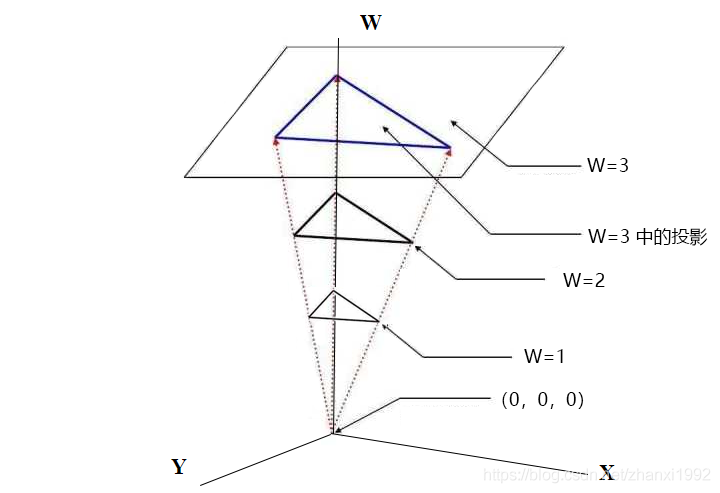
比较好的理解：

表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7)，谁知道它是个向量还是个点！

如果用齐次坐标————上面的(1, 4, 7)如果写成（1,4,7,0），它就是个向量；如果是(1,4,7,1)，它就是个点。因此可以用齐次坐标很好的将向量和点统一起来表示。

详见：https://blog.csdn.net/wonengguwozai/article/details/126123349

线性变换

线性变换包括：欧式变换Euclidean、仿射变换affine和透视变换projective。

欧式变换Euclidean

欧式变换保持了长度和角度，平移和旋转是欧式变换。也叫刚体变换。

平移

将一个点从一个位置转换到另一个位置

其中：

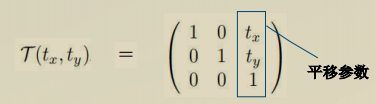
推广到三维：

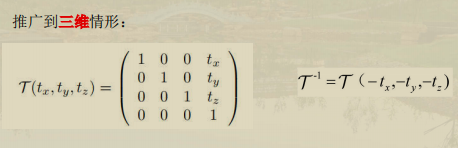
旋转

推广到三维：

仿射变换affine

仿射变换保持了长度和角度的比值，仿射变换的例子是剪切和缩放。

缩放

剪切

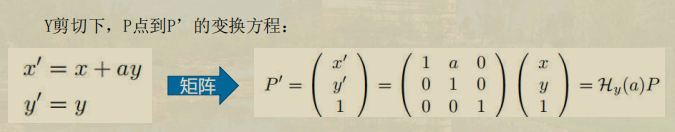
透视变换projective

透视变换可以来实现有限范围的点变换为无穷远点，将图像投影到一个新的视平面（也叫投影变换）

图像成像

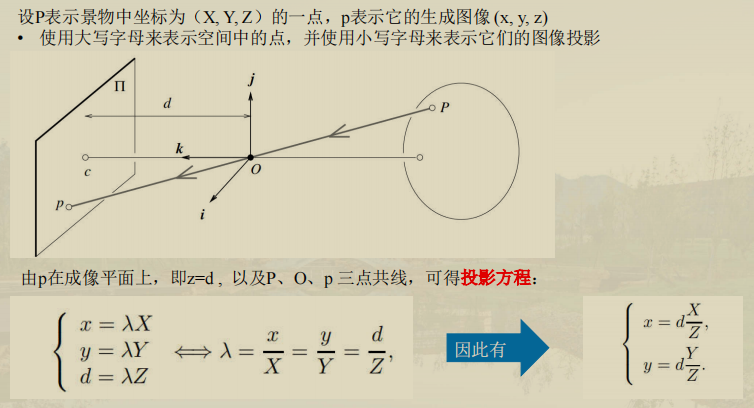
针孔透视

针孔模型中，光线通过一个无限小的孔，并且在成像平面上呈现出倒像。

**透视投影：**将三维物体的信息映射到二维平面上。

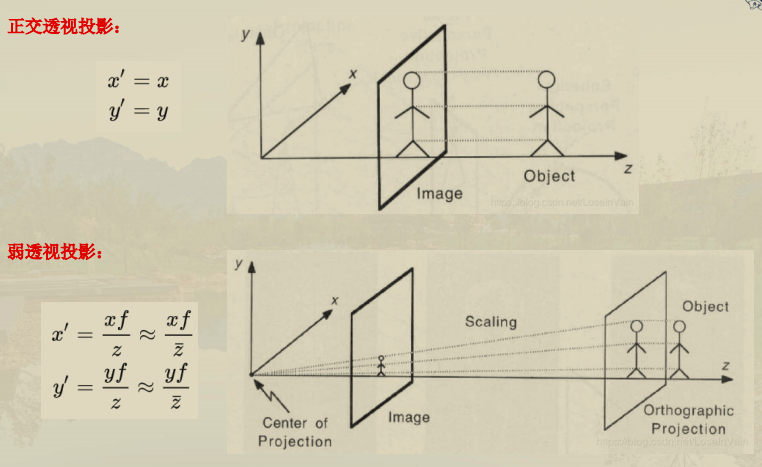
弱透视

弱透视投影：平面中的所有线段都以相同的放大倍数进行投影。

相机事实上成像在后面，然后取倒像

摄像机镜头

Snell定律

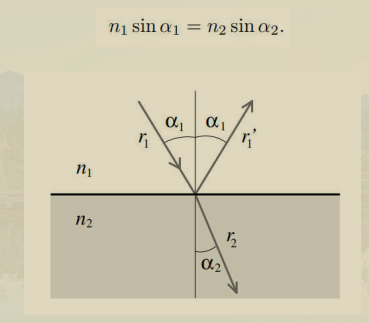
薄透镜

厚透镜

z是镜到cmos的距离，Z是物体到镜的距离

相机的视野

相机的视野：即实际投影到相机视网膜上的景物部分，不仅由焦距定义，还取决于视网膜的有效面积（例如，相机中可曝光的胶片面积，或数码相机中的传感器面积)。

球形像差

简单地说：就是大光圈进光亮大造成虚化。

标准答案：

球形像差，顾名思义是由于透镜的球形表面造成的像差。实际上，球面镜不能将所有光线聚焦在同一点，透过镜片边缘进入的光线会偏离焦点形成像差。尤其在大光圈的时候，有较多光线可以通过镜片。最明显就是一些光点会虚化成一团光，这是由于边缘位置进入的光线与中心聚焦的偏差较大所致。

色差

不同波长（颜色）的光线由于折射系数的差异（色散），在通过透镜时将发生不同程度的折射然后与光轴相交于不同的位置，并在同一图像平面上形成不同的模糊圈（横向色差）。

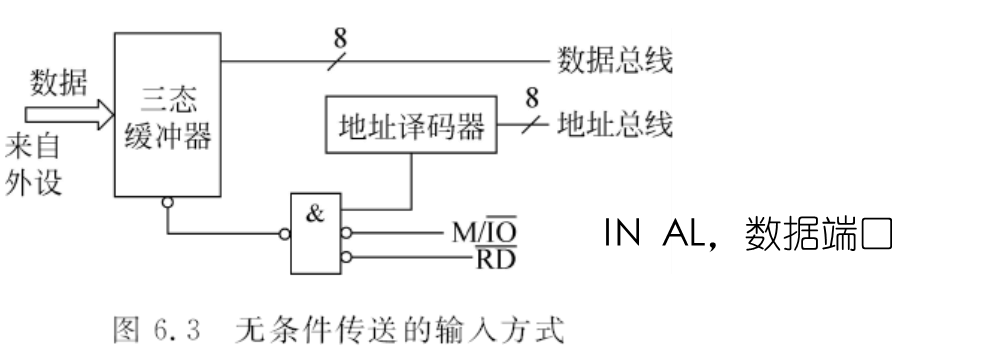
摄像机的几何标定

内参矩阵

在u和v方向上分辨率分别为mu和mv，tu和tv是平移量。

外参矩阵

相机的投影中心不在（0，0，0），主轴不在Z轴上，图像平面虽然仍然与主轴正交，但也不平行于XY平面。

设这个平移矩阵为T(Tx, Ty, Tz)。让主轴与Z轴重合的旋转矩阵由3×3旋转矩阵R给出，子矩阵（RT是平移矩阵）相乘得到3×4变换矩阵。

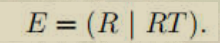
E被称为外参矩阵。

相机标定矩阵

张正友标定法

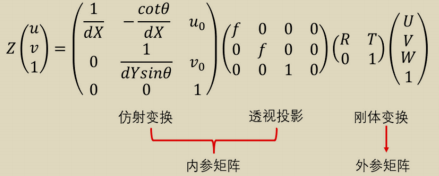
1.求解内参矩阵和外参矩阵的积H

当一张图片上的标定板角点数量等于4时，即可求得该图片对应的矩阵H 。当一张图片上的标定板角点数量大于4时，利用最小二乘法回归最佳的矩阵H 。

最小二乘法:简单地说就是通过n组X（u，v）和Y（U，V），求解八个参数。

https://blog.csdn.net/W1995S/article/details/118153146

2.求解内参矩阵

3.求解外参矩阵

4、标定相机的畸变参数

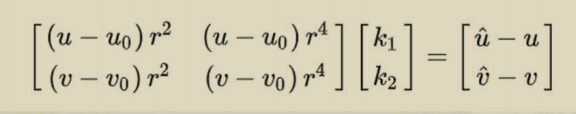
r为图像像素点到图像中心点的距离，即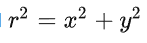

在这里，x->u y->v