前端展示的优化

面对数据量大的情况，可以采用以下优化方法：

1. 数据库优化：对数据库进行优化，包括索引优化、表结构优化、SQL语句优化等，可以提高数据库的查询效率。

2. 缓存优化：使用缓存技术，将经常访问的数据缓存到内存中，可以减少数据库的访问次数，提高系统的响应速度。

3. 分布式架构：采用分布式架构，将数据分散到多个节点中，可以提高系统的并发能力和可扩展性。

4. 压缩技术：对数据进行压缩，可以减少数据的存储空间，提高数据的传输效率。

5. 异步处理：采用异步处理技术，将数据处理任务分解成多个子任务并行处理，可以提高系统的处理能力和响应速度。

6. 数据分片：将数据按照一定规则分成多个片段，可以提高数据的并发访问能力和查询效率。

7. 数据清洗：对数据进行清洗和去重，可以减少数据量，提高数据的质量和查询效率。

综上所述，针对数据量大的情况，可以采用多种优化方法，以提高系统的性能和响应速度。

后端算法的支持

1. 分治算法

简介

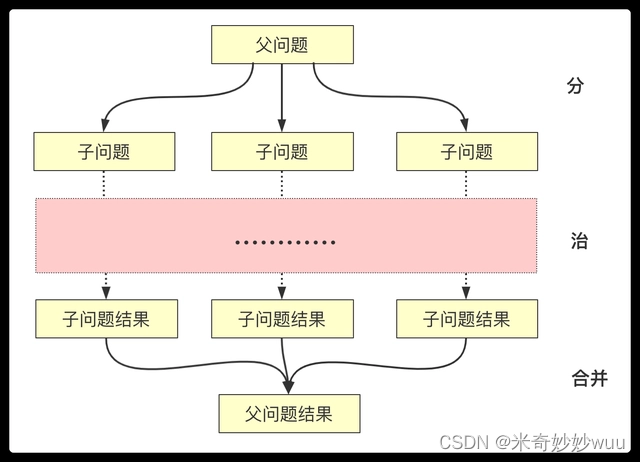
分治算法是一种递归式的算法思想，它将一个大问题分解成若干个小问题，然后递归地解决每个小问题，最后将所有小问题的解合并起来得到大问题的解。

基本步骤

分治算法的基本步骤如下：

1. 分解问题：将原问题分解成若干个子问题，每个子问题的解都与原问题的解具有相同的结构，但规模更小。

2. 解决子问题：递归地解决每个子问题，如果子问题的规模足够小，则直接求解。

3. 合并解：将所有子问题的解合并起来得到原问题的解。

关键点

实现分治算法的关键在于如何分解问题和合并解。通常情况下，分解问题的方法是将原问题分成两个或多个规模相同或相似的子问题，而合并解的方法则是将子问题的解合并起来得到原问题的解。

举例

例如，归并排序就是一种典型的分治算法，它的实现步骤如下：

1. 分解问题：将待排序的数组分成两个规模相等的子数组。

2. 解决子问题：递归地对每个子数组进行排序，如果子数组的长度为1，则直接返回。

3. 合并解：将两个已排序的子数组合并成一个有序的数组。

总结

在实现分治算法时，需要注意递归的终止条件和子问题的规模。如果子问题的规模太小，则递归的效率会变得很低，甚至可能导致栈溢出等问题。因此，需要根据具体问题的规模和复杂度来确定递归的终止条件和子问题的规模。

2. 哈希算法

简介

哈希算法是一种将任意长度的消息压缩到某一固定长度的算法。它将输入数据（也称为消息）映射到固定长度的哈希值，通常是一个固定长度的二进制字符串。

特点

哈希算法具有以下特点：

1. 输入数据的任何细微变化都会导致哈希值的巨大变化。
2. 哈希值的长度是固定的，不受输入数据长度的影响。
3. 哈希算法是单向的，即无法从哈希值推导出原始数据。

哈希算法可以用于解决海量数据问题，例如在海量数据中查找某个特定的数据项。一种常见的方法是使用哈希表，将数据项的哈希值作为索引存储在哈希表中。当需要查找某个数据项时，先计算其哈希值，然后在哈希表中查找对应的索引，最终找到该数据项。

应用

使用哈希算法解决海量数据问题需要注意以下几点：

1. 哈希函数的设计要尽可能避免冲突，即不同的数据项计算出相同的哈希值。
2. 哈希表的大小要合适，既不能太小导致冲突过多，也不能太大导致浪费空间。
3. 对于哈希冲突的情况，需要使用合适的解决方法，例如链表法或开放地址法。

3. 位图（BitMap ）算法

简介

BitMap 算法是一种基于位运算的数据压缩算法，可以用来解决海量数据问题。它的基本思想是将数据映射到一个位图中，用 0 或 1 表示某个元素是否存在，从而实现对数据的快速查询和统计。

实现步骤

具体来说，BitMap 算法的实现步骤如下：

1. 创建一个位图，位图的大小为数据中最大值加 1。

2. 遍历数据，将每个元素对应的位图位置为 1。

3. 查询某个元素是否存在，只需要在位图中查找对应位置的值即可。

4. 统计数据中有多少个不同的元素，只需要遍历位图，统计值为 1 的位数即可。

BitMap 算法的时间复杂度为 O(n)，空间复杂度为 O(max)，其中 max 表示数据中的最大值。因此，BitMap 算法适用于数据量大，但数据范围较小的场景，比如 IP 地址统计、布隆过滤器等。

需要注意的是，BitMap 算法只适用于数据元素为非负整数的情况，对于其他类型的数据需要进行转换才能使用。

4. 布隆过滤器（Bloom Filter）

简介

布隆过滤器（Bloom Filter）是一种空间效率非常高的随机数据结构，它利用位数组和哈希函数实现，可以用于判断一个元素是否在一个集合中。它的主要优点是空间效率和查询时间都比较优秀，缺点是有一定的误判率。

工作流程

1. 初始化：创建一个长度为m的位数组，并将所有位都初始化为0。

2. 添加元素：将元素通过k个哈希函数映射到位数组中的k个位置上，并将这k个位置的值都设为1。

3. 查询元素：将要查询的元素通过k个哈希函数映射到位数组中的k个位置上，如果这k个位置的值都为1，则说明该元素可能存在于集合中；如果这k个位置中有任意一个位置的值为0，则说明该元素一定不存在于集合中。

总结

布隆过滤器可以解决海量数据问题，因为它只需要占用很少的内存空间，就可以判断一个元素是否在一个集合中。在实际应用中，可以将布隆过滤器用于缓存、黑名单过滤、爬虫去重等场景，可以大大提高系统的效率和性能

5. 堆排序

堆排序是一种基于二叉堆数据结构的排序算法。

工作流程

1. 将待排序的序列构建成一个大根堆或小根堆；
2. 将堆顶元素（最大值或最小值）与堆底元素交换；
3. 重新调整堆，使其满足堆的性质；
4. 重复步骤2和3，直到整个序列有序。

堆排序的时间复杂度为O(nlogn)，空间复杂度为O(1)。

总结

对于海量数据问题，可以采用外部排序的方法。外部排序是一种针对大规模数据的排序算法，它将数据分成若干个小块，每次只处理一部分数据，最后将所有小块合并成一个有序的序列。常用的外部排序算法有归并排序和快速排序。在实际应用中，可以将数据分成多个块，每次只处理一部分数据，然后将处理后的数据写入磁盘，最后再将所有块合并成一个有序的序列。这样可以避免将所有数据读入内存，从而解决海量数据问题。。