C语言学习后，曾为先学C++还是数据结构纠结了半天。在看数据结构前言的时候，发现学习数据结构之前还需要一定的数学基础。虽然涉及到的数学基础不多，但想到以前大学高数，现代不是60分万岁就是不到80分，好像就概率论稍微了解得多一些，因为那个时候玩游戏会用到概率的问题……不仅如此，现在已经毕业10年，因此尽管时间已经相当紧迫，我还是决定先花一段时间巩固数学基础。学习高等数学，线性代数，概率论，离散数学，毕竟磨刀不误砍柴工。
因为是纯理论不像C语言那样需要上机编程，因此学习过程中主要是截图老师的板书。（避免久坐不动打瞌睡）。

映射

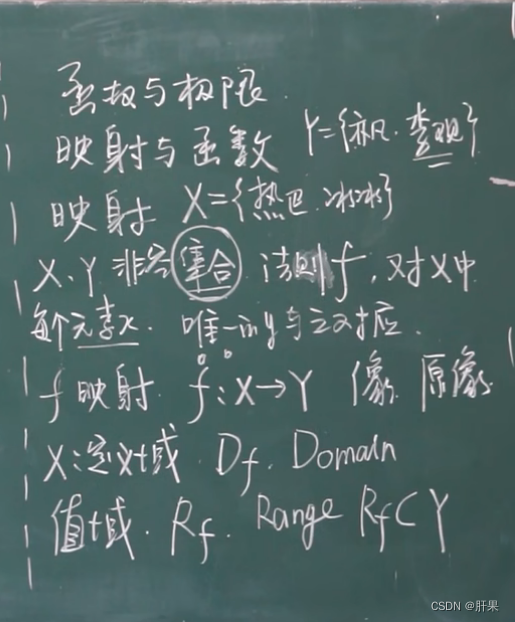
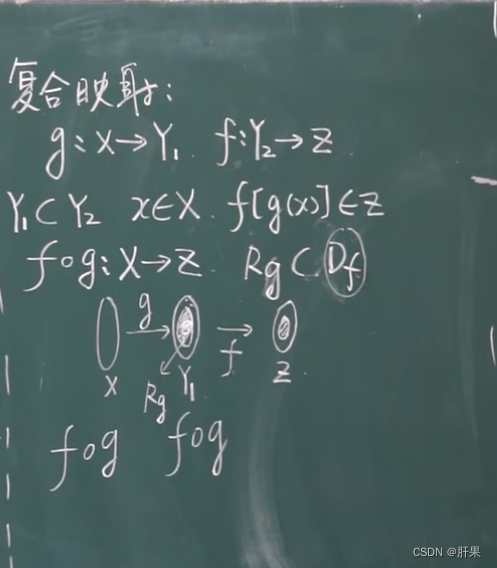
函数是特殊的映射，映射是特殊的对应

函数

在数学中，无理数是指不能表示为两个整数的比的数。无理数是实数的一个子集，它们不能被表示为一个有理数（即可以表示为两个整数的比）的形式。

最早证明存在无理数的是古希腊数学家毕达哥拉斯，他们发现2的平方根不能表示为两个整数的比，这个发现颠覆了他们完美的有理数理论。同时，他们也发现了勾股定理的几何应用，强调了几何学在数学中的重要地位。

无理数的代表有圆周率$\pi$、自然对数的底数$e$等等，常见的无理数都不能表示成一个有限小数或无限循环小数的形式，比如$\pi$可以写成无限小数$\mathrm{3.1415926535897932...}$的形式。

需要注意的是，对于计算机来说，由于计算机是离散的，虽然可以表示有理数，但是很多无理数都只能进行近似计算。

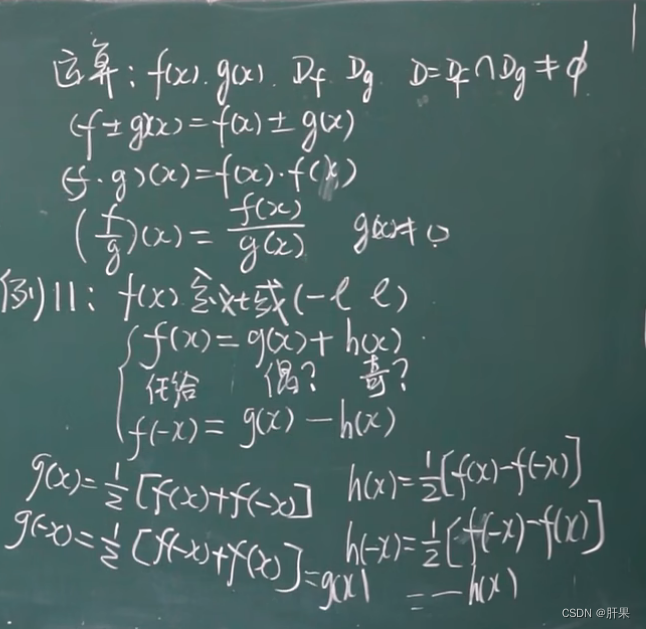
初等函数：

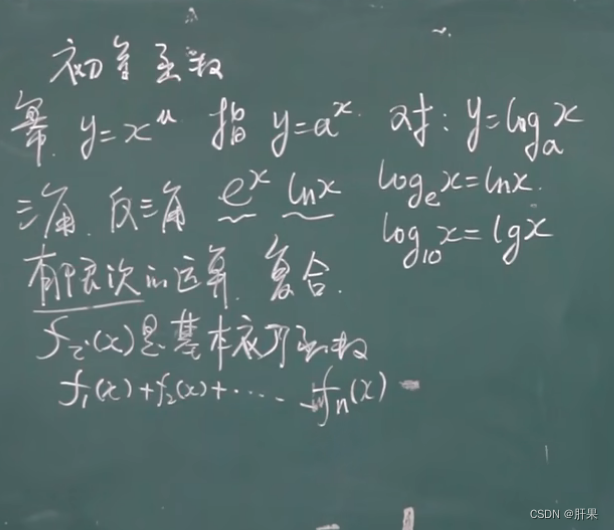
数列极限的定义

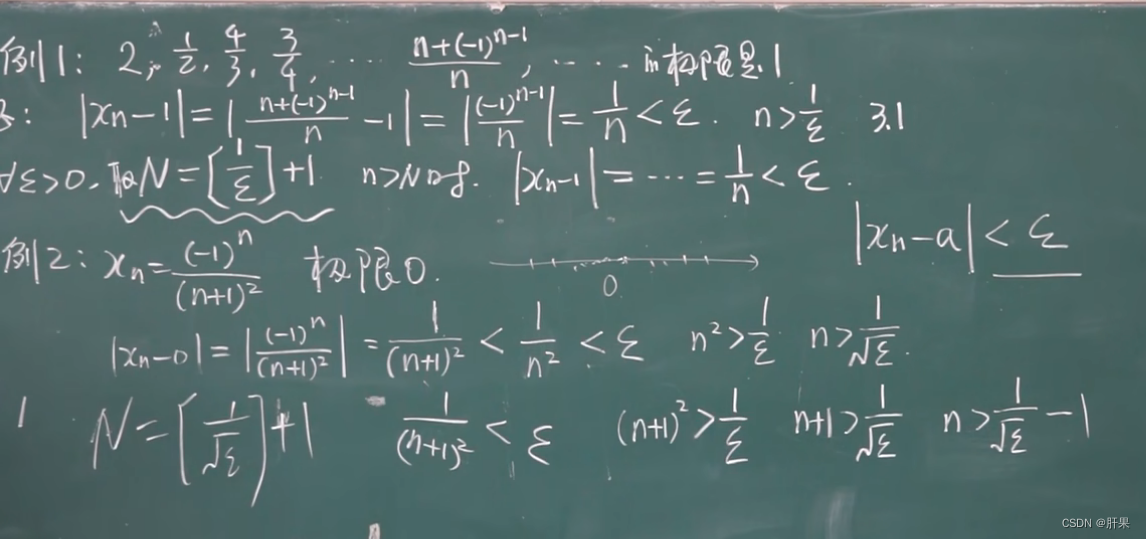
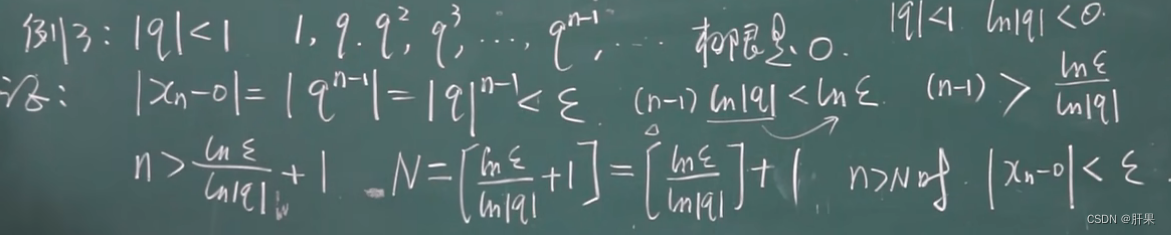
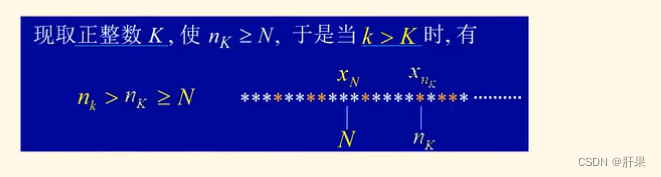
反三角函数

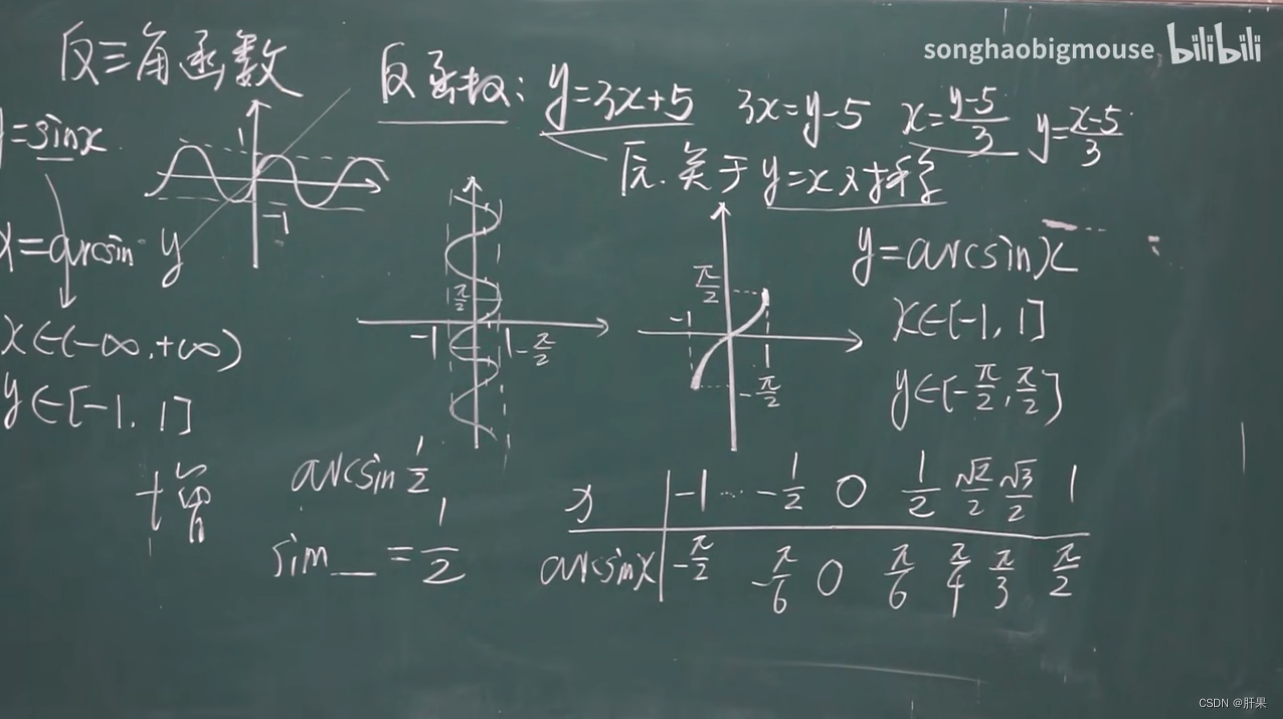
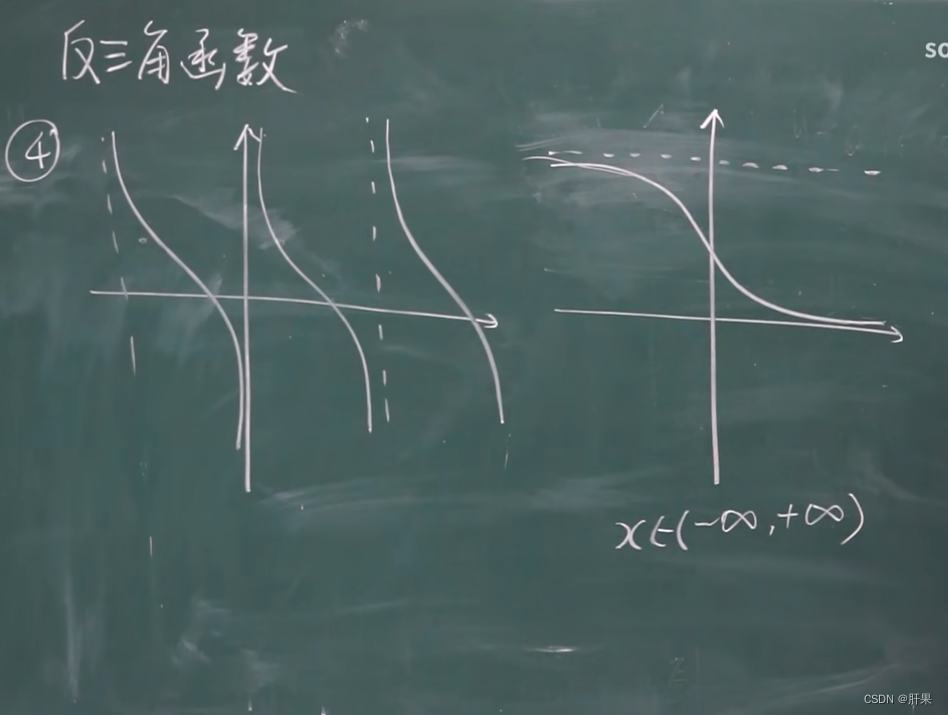
正切函数 $\tan x$ 是三角函数 $\sin x$ 和 $\cos x$ 的比值，即 $\tan x=\frac{\sin x}{\cos x}$。

在直角三角形中，正切函数可以定义为对边与邻边的比值，即 $\tan x=\frac{o}{a}$，其中 $o$ 表示对边，$a$ 表示邻边。

通过这个定义，我们可以发现正切函数与正弦函数和余弦函数之间的关系：

$$\tan x=\frac{\sin x}{\cos x}=\frac{o}{a}$$

从上式中可以发现，当夹角 $x$ 为锐角或直角时，$\cos x$ 不为零，且 $\sin x$ 与 $\cos x$ 的符号相同，因此 $\tan x$ 的结果为正数。

当夹角 $x$ 为钝角时，$\sin x$ 与 $\cos x$ 的符号相反，因此 $\tan x$ 的结果为负数。

因此，可以得出结论：在锐角和直角下，$\tan x$ 和 $\sin x$、$\cos x$ 之间的符号相同，但在钝角下，它们的符号相反。

函数的极限

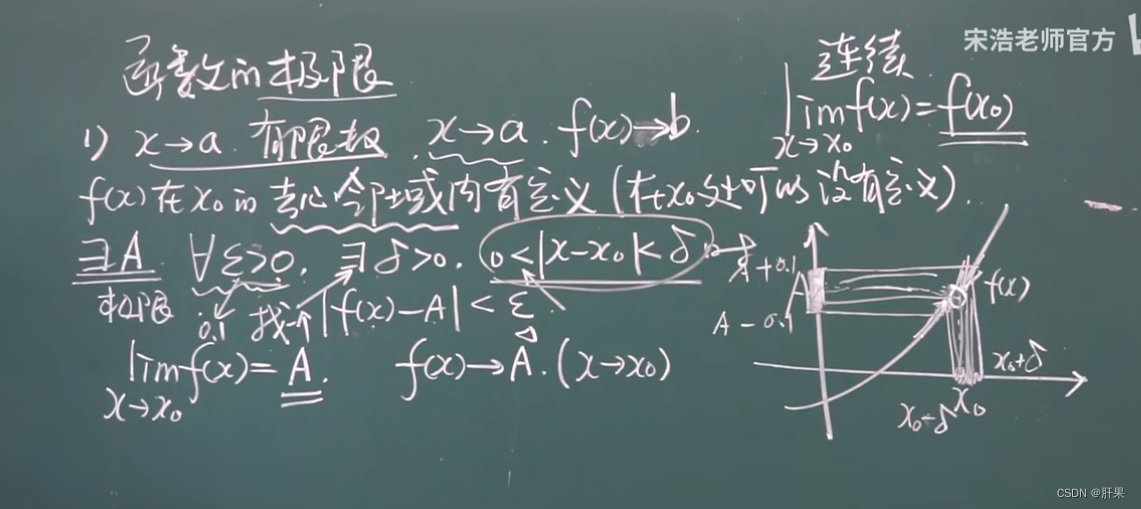
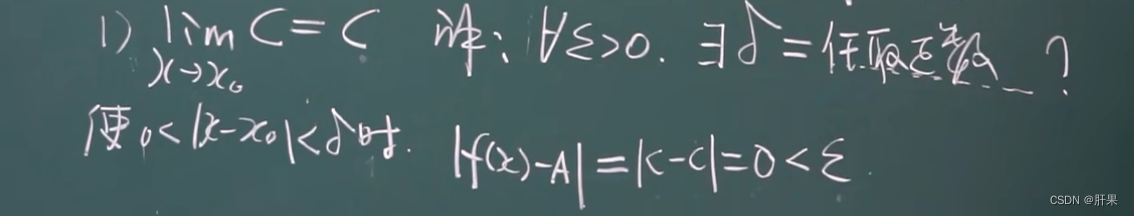
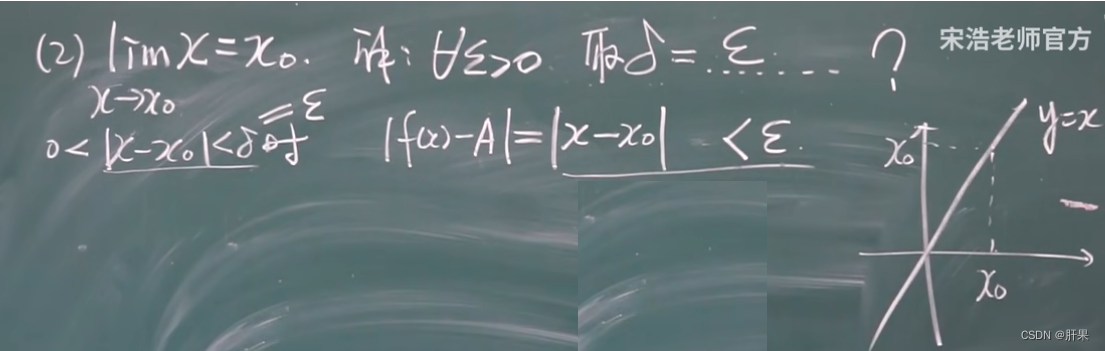
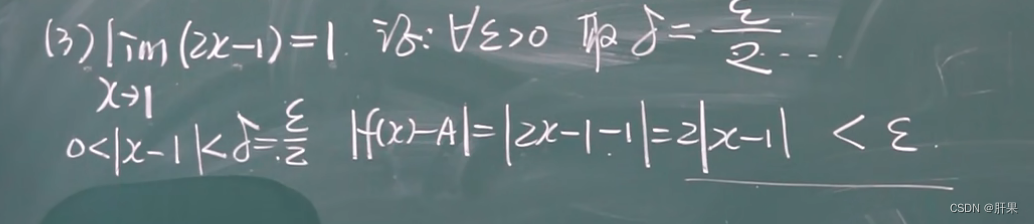
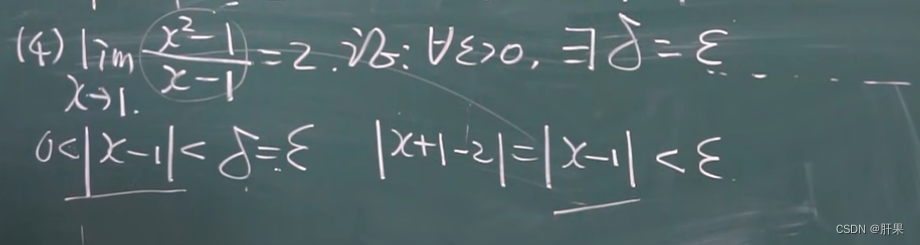
相对重要的知识点：

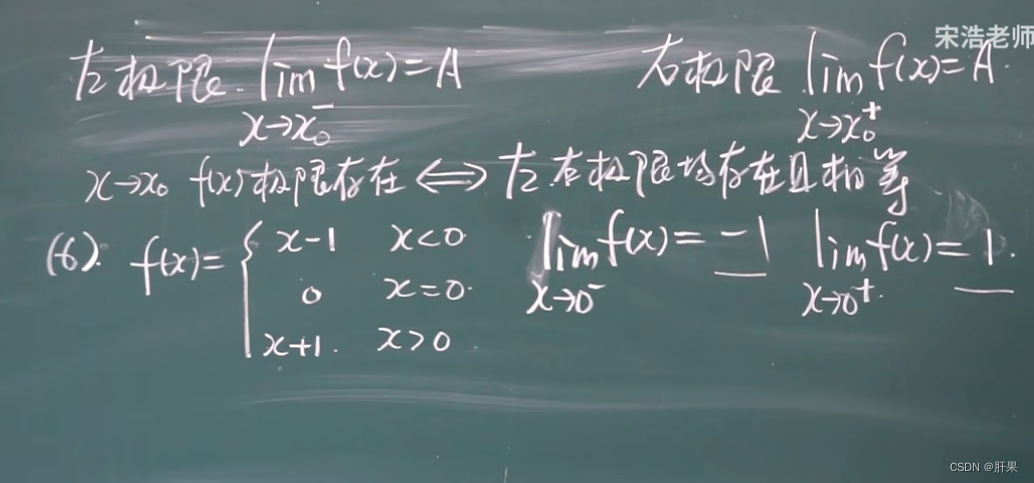
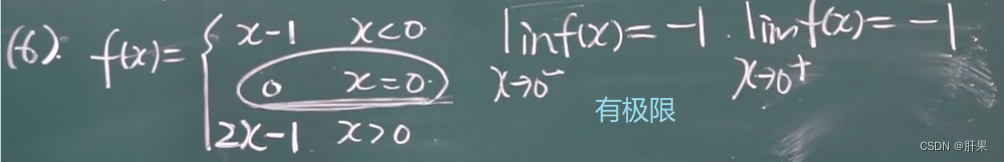
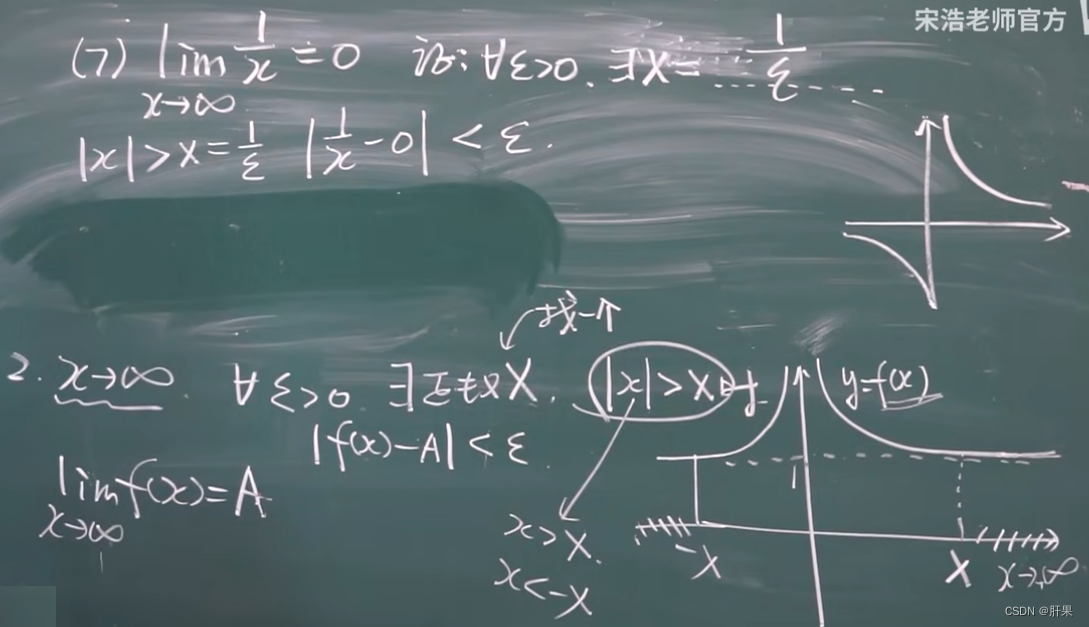
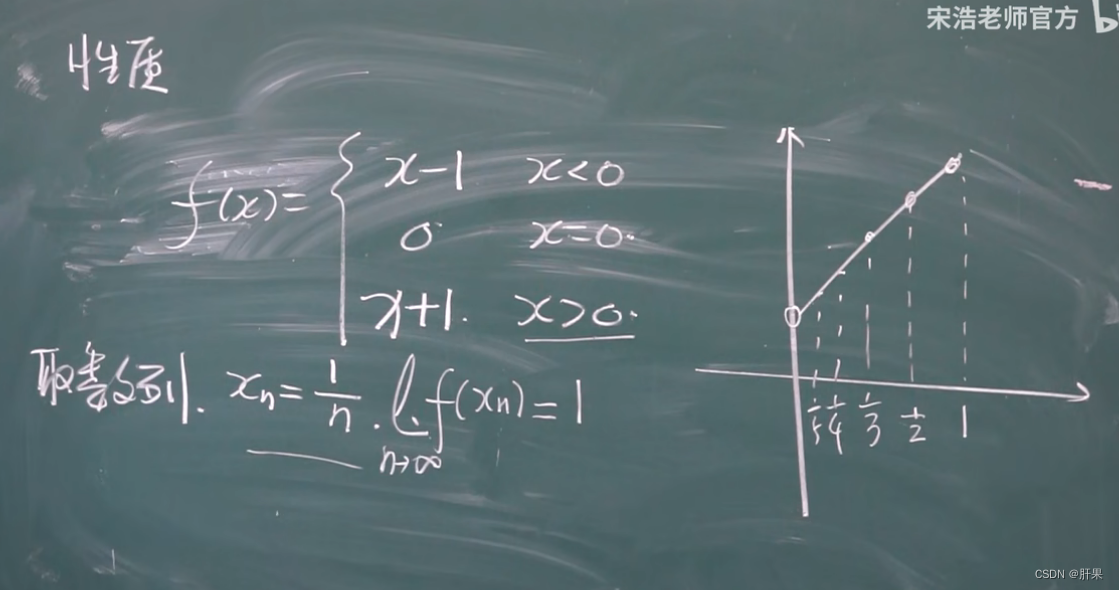
无穷小与无穷大

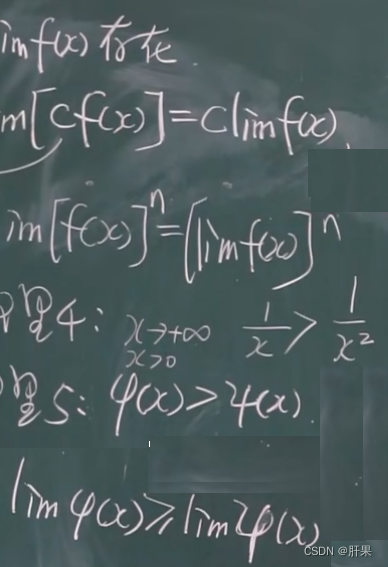
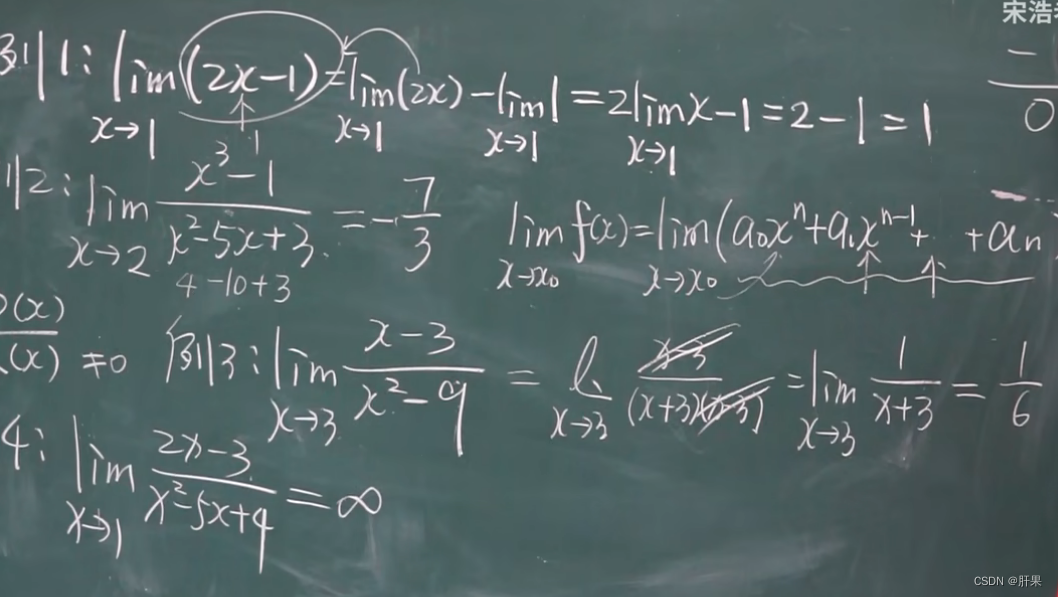
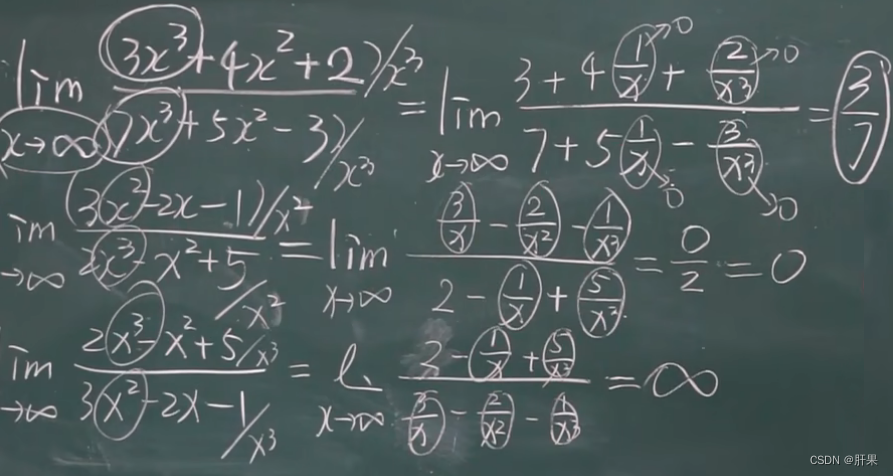
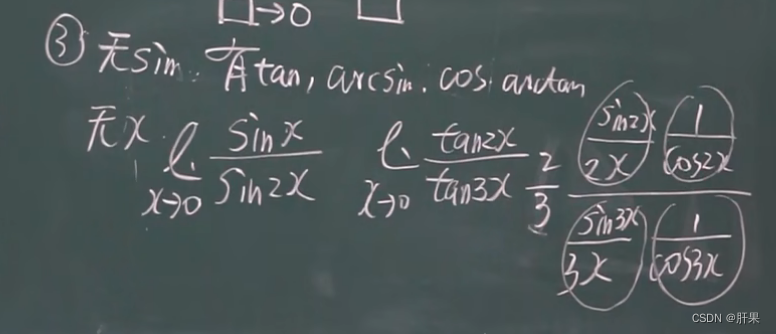
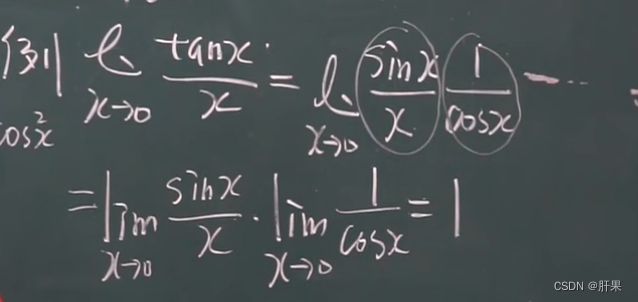
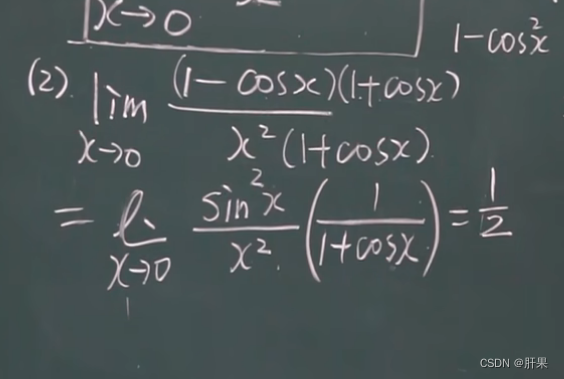
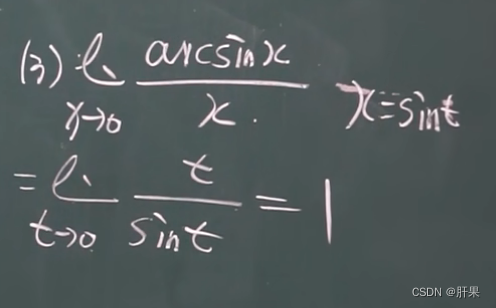
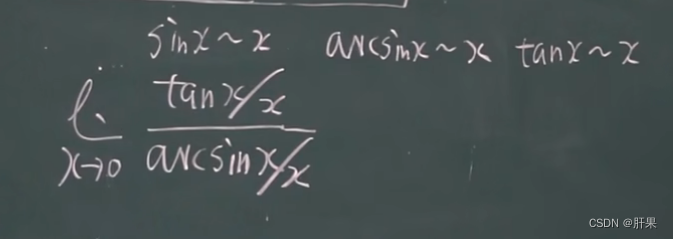
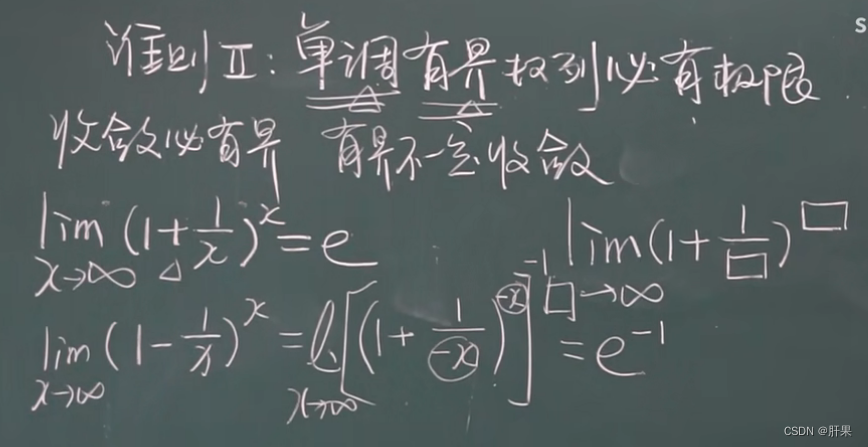
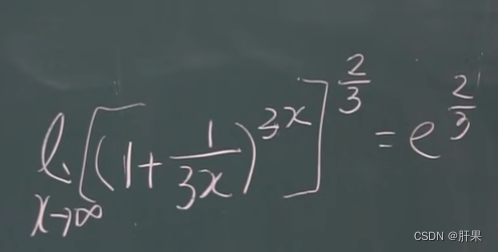
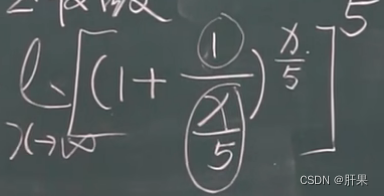
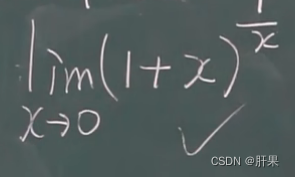
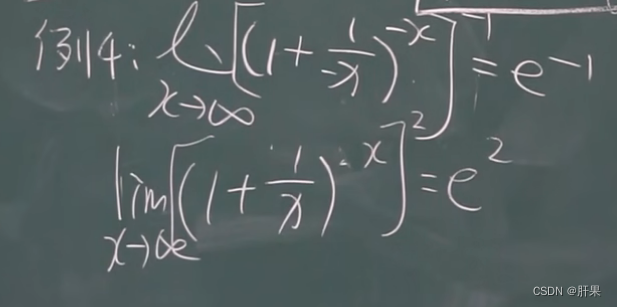
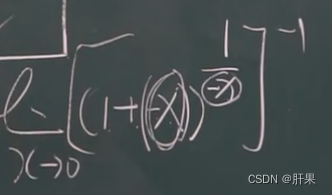
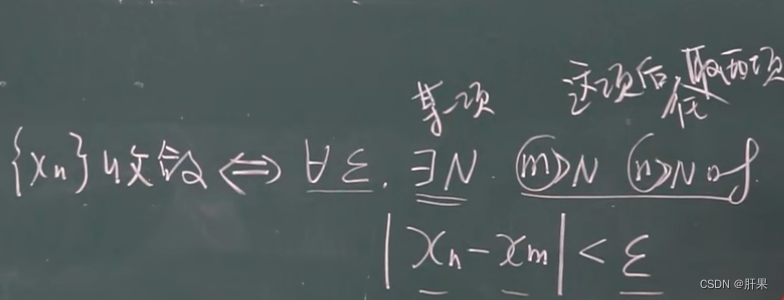
无穷小的比较



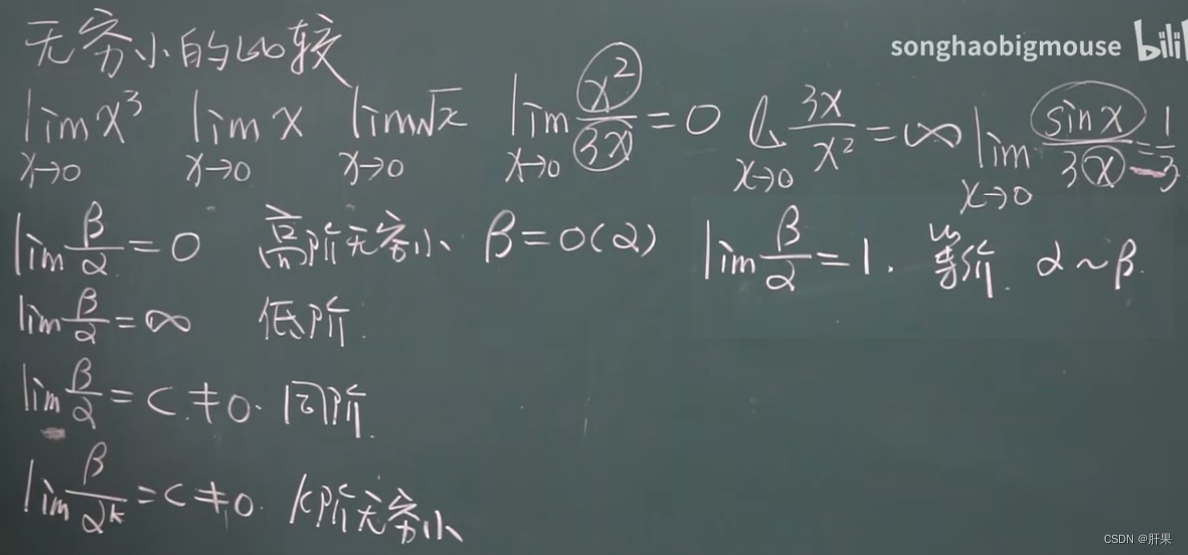
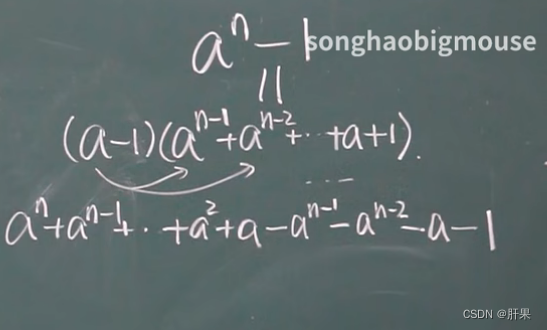
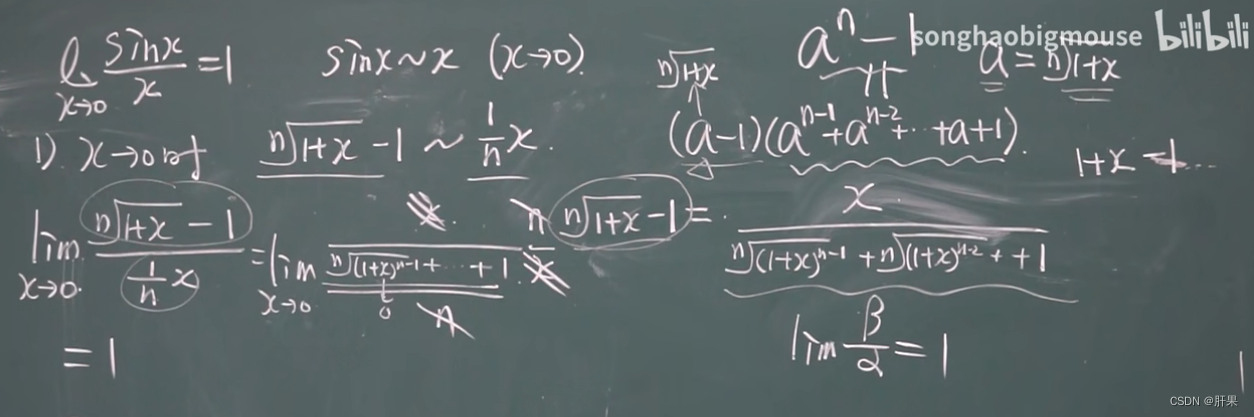
以下等价：

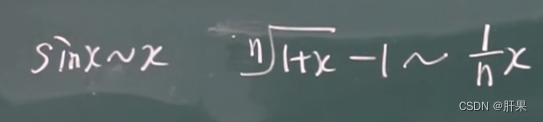
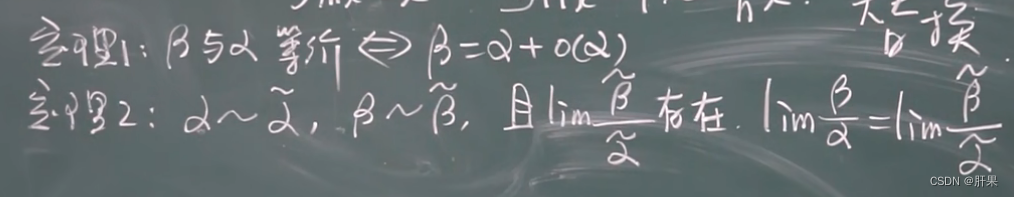
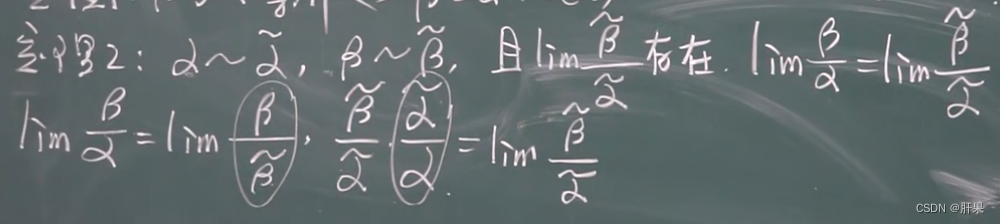
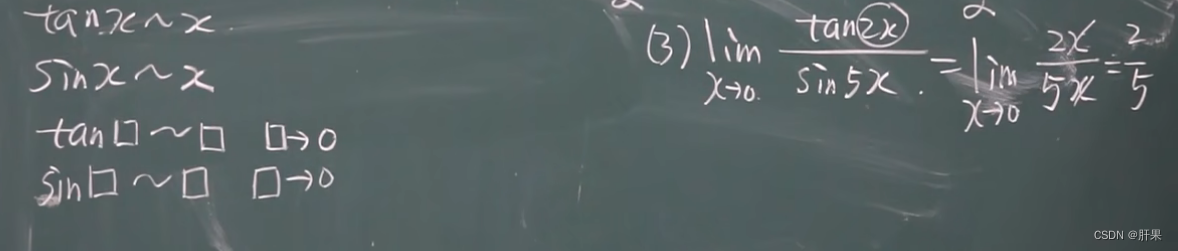
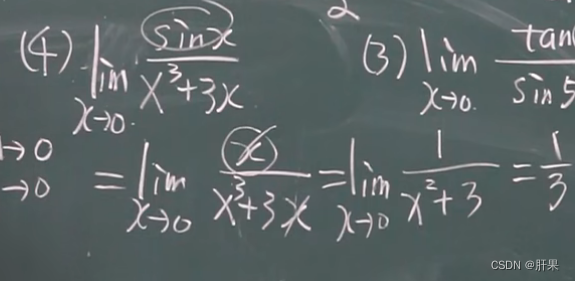
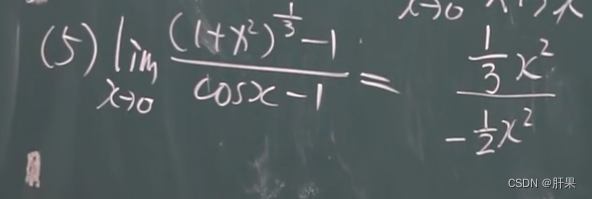
连续性

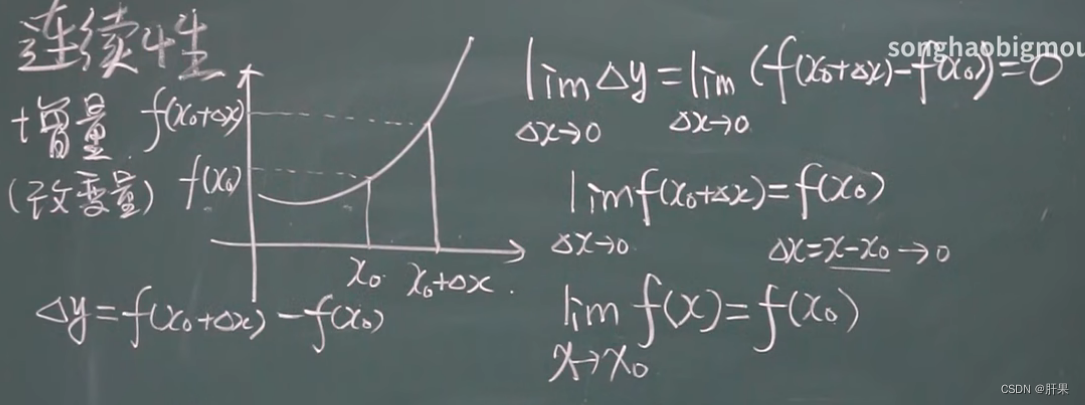
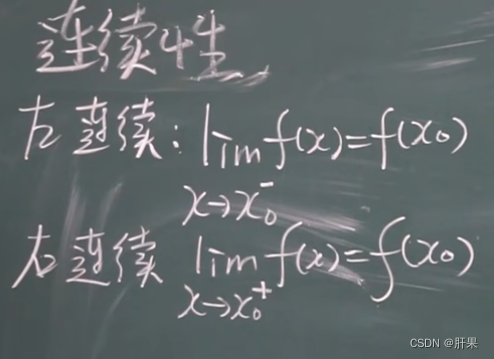
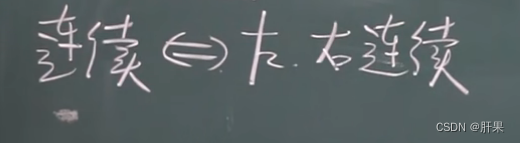
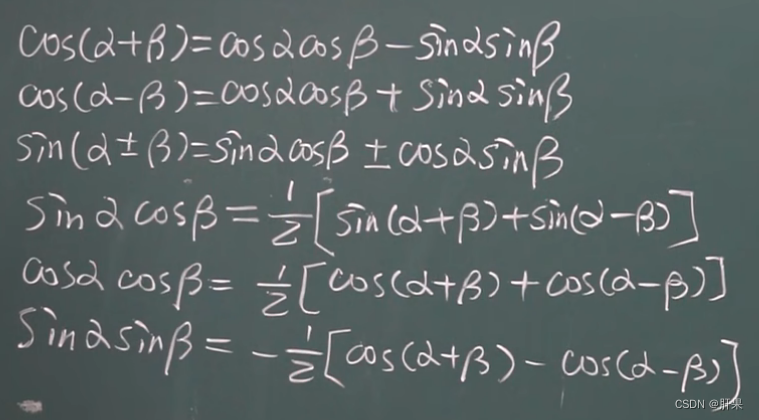
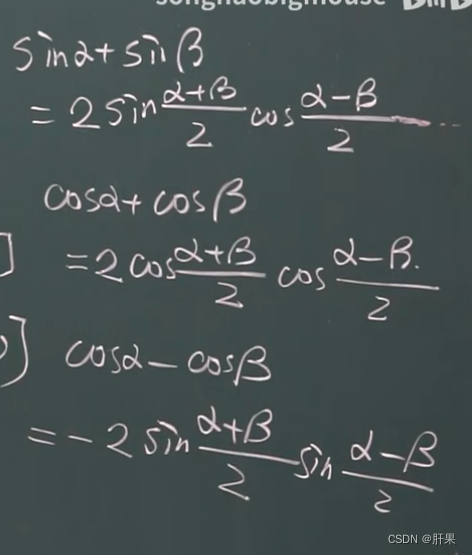
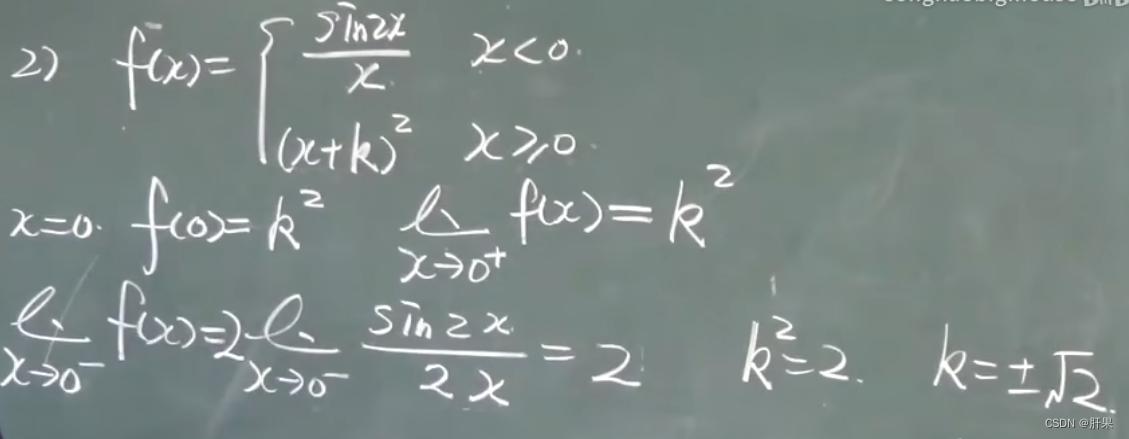
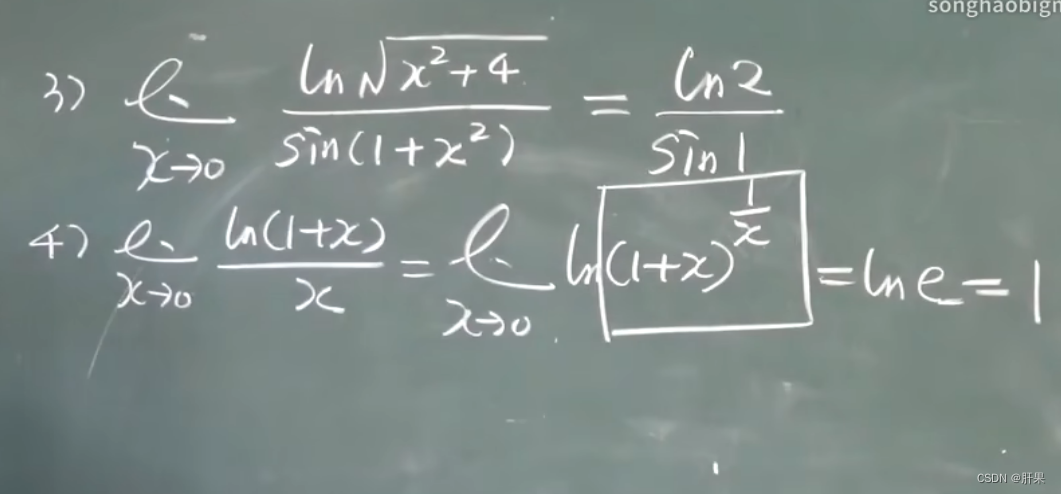
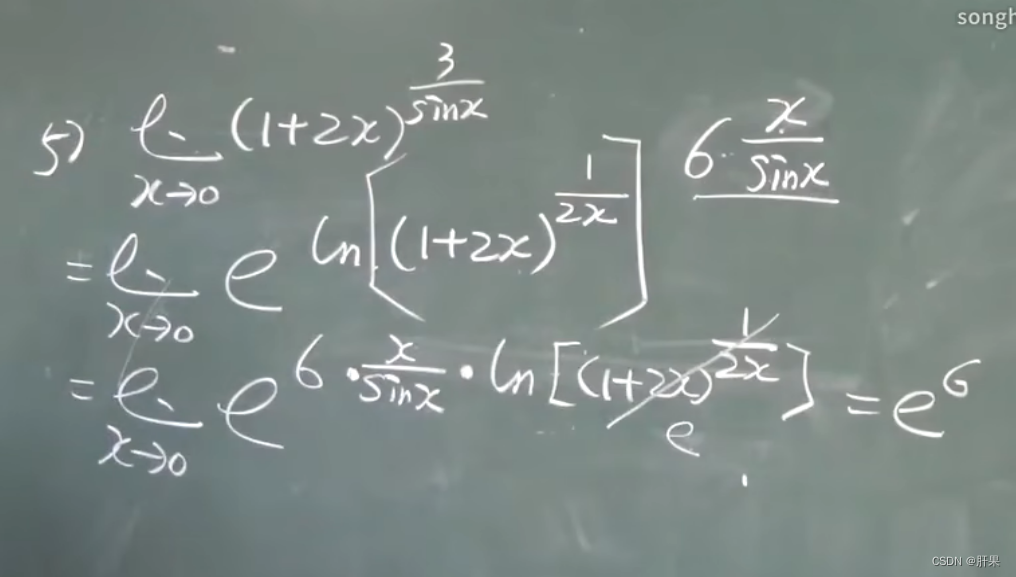
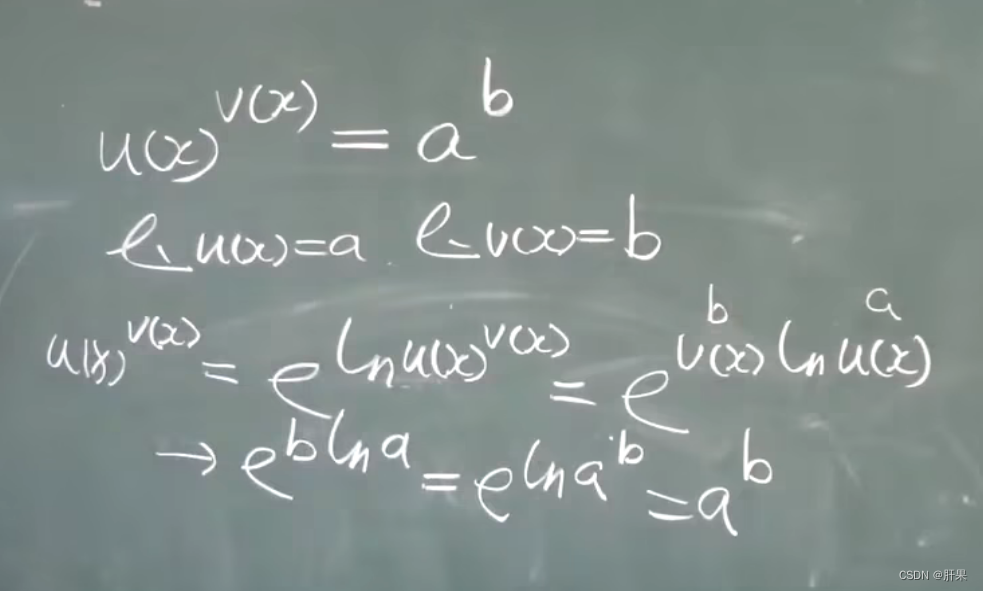
闭区间上连续性质

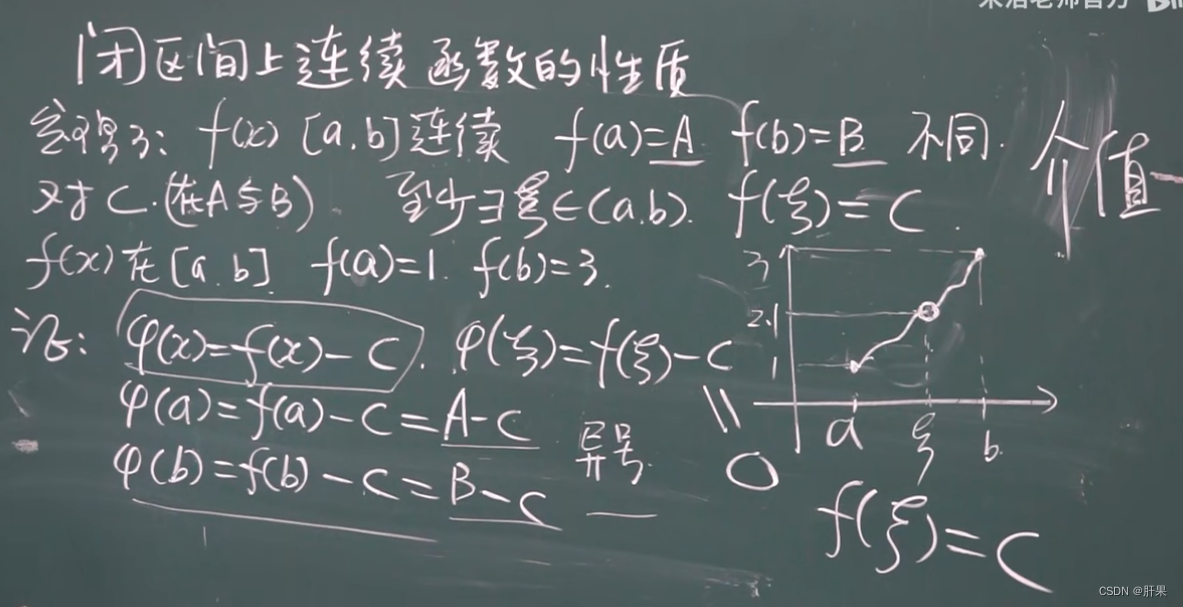
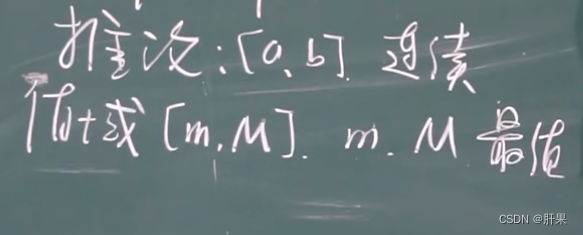
根据最值存在定理，如果一个函数$f(x)$在闭区间$[a,b]$上连续，则$f(x)$在该区间上必定存在最大值$M$和最小值$m$。同时，值域为$[m,M]$，也就是说，函数的所有取值都在$m$和$M$之间。

因此，如果一个函数在闭区间$[a,b]$上连续且值域为$[m,M]$，那么$m$和$M$分别就是函数的最小值和最大值。