目录
一、进位计数制
二、信息编码
三、定点数数据表示
四、校验码
五、定点数补码加减运算
六、标志位的生成
七、定点数的移位运算
八、定点数的乘除运算
九、浮点数的表示
十、浮点数的运算
一、进位计数制
整数部分:
- 二进制、八进制、十六进制 ---> 十进制:加权求和
- 二进制 ---> 八进制:每三位分为一组,转为八进制数
- 二进制 ---> 十六进制:每四位分为一组,转为十六进制数
- 十进制 ---> 二进制:除2取余,先得到低位
- 十进制 ---> 八进制、十六进制:先转为二进制,再转为八进制数或十六进制数
小数部分:
- 十进制转换为任意进制:乘积取整法,结果不能得到准确值,则取精度值
- 二进制 ---> 八进制、十六进制:与整数部分类似
- 二进制 ---> 十进制:加权求和
- 八进制、十六进制 ---> 十进制:先转为二进制,再转为十进制
真值:符合人类习惯的数字
机器数:数字实际存在机器里的形式
二、信息编码
BCD码:Binary Coded Decimal,二-十进制码,即用二进制数表示十进制数。
BCD码分为有权码和无权码。常见的有权码有8421码、2421码、84-2-1码,常见的无权码有格雷码、余三码。
有权码的共性:都是自补码,即任意两个和为9的编码,互为补码。
格雷码:任何相邻的两个编码之间只有一位二进制位不同。
余三码:每个编码都是其8421码加上0011所得。
三、定点数数据表示
原码
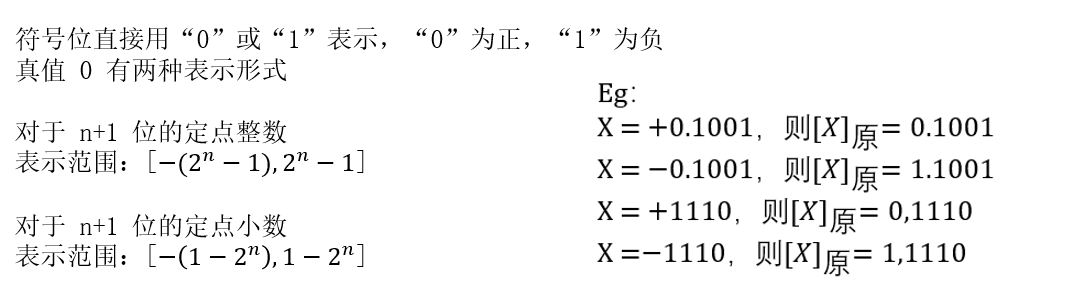
反码

补码

移码
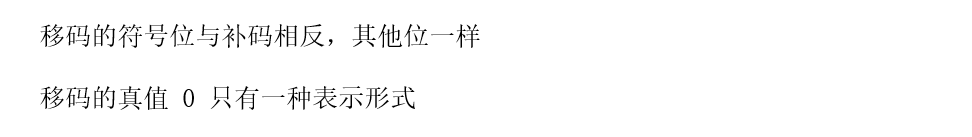
四、校验码

奇偶校验码:奇校验位的取值应该使整个奇校验码中“1”的个数为奇数,偶校验码的取值应该使整个偶校验码中“1”的个数为偶数
奇偶校验码的码距为2,具有检查一位错误或奇数位错误的能力。
五、定点数补码加减运算

六、标志位的生成
OF:Overflow Flag bit,溢出标志位(只对有符号数加减有意义)
SF:Sign Flag bit,符号标志位(只对有符号数加减有意义)
ZF:Zero Flag bit,判零标志位
CF:Carry Flag bit,进位/借位标志位(只对无符号数加减法有意义)
PF:Parity Flag bit,奇偶标志位
OF可以由最高位产生的进位S1和次高位产生的进位S2异或所得,即OF = S1 ⊕ S2
CF可以由最高位产生的进位S1和sub加减控制信号异或所得,即CF = S1 ⊕ sub
七、定点数的移位运算
算术移位:通过改变各个数码位与小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘法、除法。
原码的算术移位:符号位不变,仅对数值位进行移位。
右移——高位补0,低位舍弃,若舍弃不为0,丢失精度;
左移——低位补0,高位舍弃,若舍弃不为0,出现严重误差。
反码的算术移位:正数与原码一样,负数与原码不同
负数右移——高位补1,低位舍弃;
负数左移——低位补1,高位舍弃。
补码的算术移位:正数与原码、反码一样
补码是原码的反码低位加一所得,所以补码的前半部分同反码,后半部分同原码
负数右移——高位补1,低位舍弃;
负数左移——低位补0,高位舍弃。
逻辑移位:右移则高位补0低位舍弃,左移则低位补0高位舍弃,视作对无符号数处理。
循环移位:用移出去的位,补上空缺的位。带CF标志位一起的循环,称为大循环,不带则是小循环。
八、定点数的乘除运算
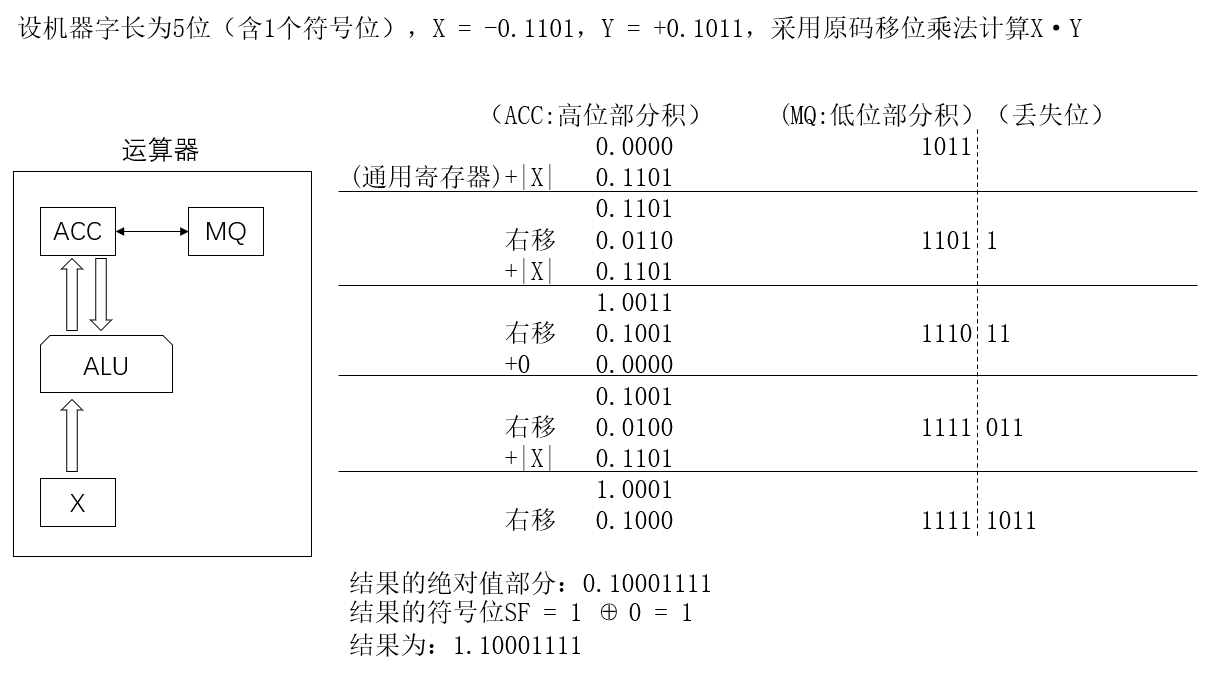
原码的乘法运算
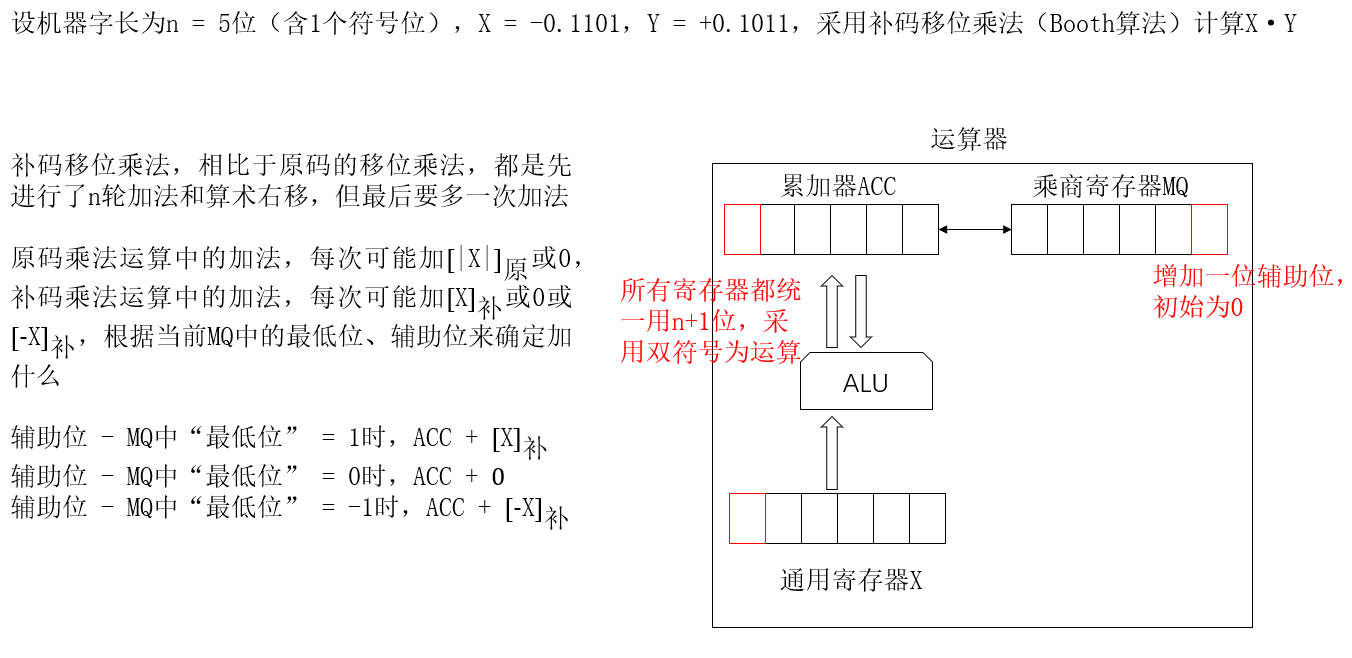
补码的乘法运算

原码的除法运算




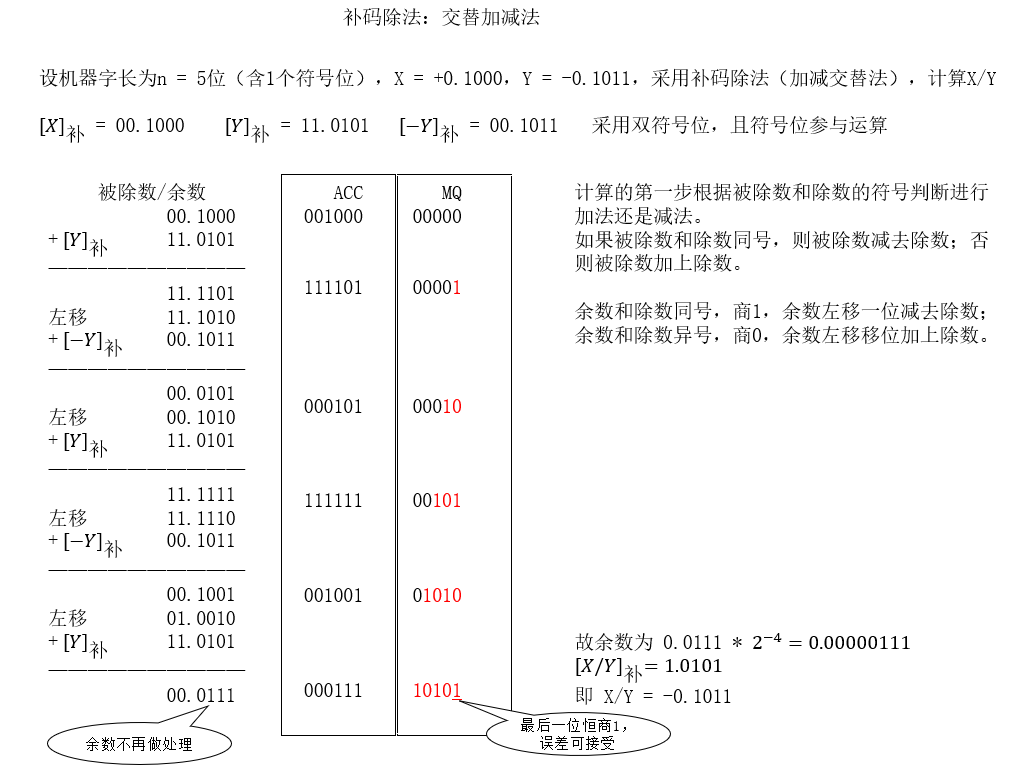
补码的除法运算
九、浮点数的表示
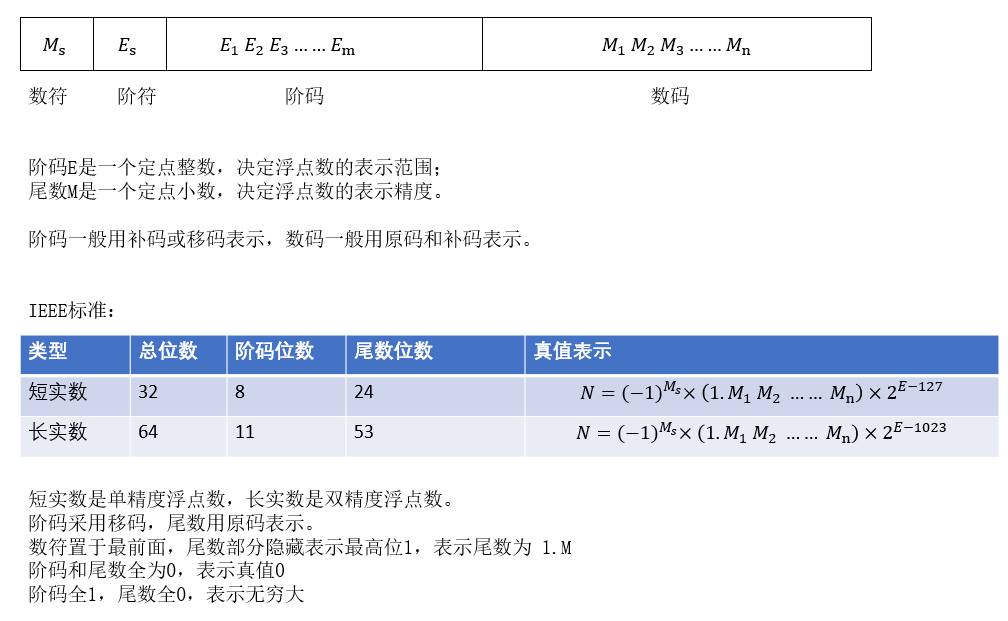
浮点数的格式
浮点数规格化

浮点数的溢出

- 出现上溢:系统中断
- 出现下溢:当作机器0处理
- 当浮点数尾数为0:当作机器0处理,无视阶码
真值与浮点数格式的转换

十进制数与单精度浮点数的转换

十、浮点数的运算
浮点数加减运算步骤
- 对阶:小阶向大阶对齐
- 尾数加减:阶数不变
- 规格化:保证尾数的第一个数值位是一个有效位
- 舍入:①截断法;②0舍1入法;③末尾恒置1法
- 判溢出:根据双符号是否一样panduan