最短路径
-
图上的最短路径:两顶点之间经过的边数最少的路径;
-
网上的最短路径:两顶点之间经过的边上权值之和最少的路径(源点->终点)。
a星算法、迪杰斯特拉算法、佛洛依德算法。
迪杰斯特拉算法
单源最短路径按路径长度递增的次序产生最短路径的算法。过程如下:
-
找到直接能到达的最短路径
-
以最短到达的终点为源点继续找能直接到达的
-
更新最短路径
需要记住路径和最短路径
-
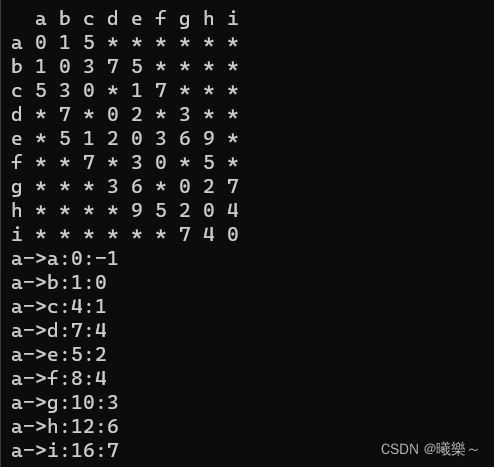
最短路径的值:shortpath[9]
-
最短路径当前顶点的前一个顶点:path[9]
-
记录顶点是否被选过:visited[9] = {0};
-
用邻接矩阵Edge存边权
-
记录当前最小值:min
-
min_index = 记录到达最短路径的下标

创建一个图:
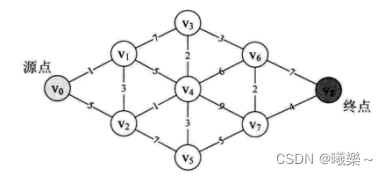
主函数:
void main()
{
Graph g;
g.InsertVertex('a');
g.InsertVertex('b');
g.InsertVertex('c');
g.InsertVertex('d');
g.InsertVertex('e');
g.InsertVertex('f');
g.InsertVertex('g');
g.InsertVertex('h');
g.InsertVertex('i');
g.InsertEdge('a', 'b', 1);
g.InsertEdge('a', 'c', 5);
g.InsertEdge('b', 'c', 3);
g.InsertEdge('b', 'd', 7);
g.InsertEdge('b', 'e', 5);
g.InsertEdge('c', 'e', 1);
g.InsertEdge('c', 'f', 7);
g.InsertEdge('d', 'g', 3);
g.InsertEdge('d', 'e', 2);
g.InsertEdge('e', 'g', 6);
g.InsertEdge('e', 'h', 9);
g.InsertEdge('e', 'f', 3);
g.InsertEdge('f', 'h', 5);
g.InsertEdge('g', 'h', 2);
g.InsertEdge('g', 'i', 7);
g.InsertEdge('h', 'i', 4);
g.PrintGraph();
g.ShortPath('a');
}单元最短路径ShortPath:
ShortPath(char vertex);输入点,从该点开始找它为起点的单元最短路径。
得到下标:
int v = GetVertexIndex(vertex);
if (v == -1) return;shortpath:最短路径的值
path:最短路径-当前顶点的前一个顶点
visited:记录顶点是否被选过
int* shortpath = new int[m_NumVertex];
int* path = new int[m_NumVertex];
int* visited = new int[m_NumVertex];初始化数组:
int i, j;
for (i = 0; i < m_NumVertex; i++)
{
shortpath[i] = m_Edge[v][i];//把权值存到shortpath中
visited[i] = 0;//没有被访问-0
if (i != v&&shortpath[i]<MAX_WEIGHT)//不是自己到自己 且 可以到达
{
path[i] = v;//可以到达,v作为其前一个顶点
}
else
path[i] = -1;//不能到达-1
}
visited[v] = 1;访问完置为1循环计算从当前顶点到其余各顶点的最短路径
min:最小权值
min_index:目的下标
int min;//min是最小权值
int min_index;//min_index是目的下标
for (i = 0; i < m_NumVertex - 1; i++)
{
min = MAX_WEIGHT;
min_index = -1;
for (j = 0; j < m_NumVertex; ++j)
{
//顶点没有被访问过 且 权值<最短路径
if (!visited[j] && shortpath[j] < min)
{
//更新最短路径和其目的下标
min = shortpath[j];
min_index = j;
}
}
//当前最短路径目的节点被访问
visited[min_index] = 1;
//更新看从min_index到其余没有找到的路经顶点的权值加上min是否小于原本的权值
//如果小则更新
for (j = 0; j < m_NumVertex; j++)
{
int w = m_Edge[min_index][j];//最短路径目的节点到其他点的权值
if (!visited[j] && w < MAX_WEIGHT&&shortpath[min_index]+w<shortpath[j])
{
shortpath[j] = shortpath[min_index] + w;
path[j] = min_index;
}
}
}输出-释放
for (i = 0; i < m_NumVertex; i++)
{
cout << vertex << "->" << m_VertexArr[i] <<
":" << shortpath[i] << ":" << path[i];//起点->终点:权值:前一个顶点下标
cout << endl;
}
delete[]shortpath;
delete[]path;
delete[]visited;
shortpath = nullptr;
path = nullptr;
visited = nullptr;