斐波那契数列题解（非递归c++方法实现）

news2024/12/28 2:47:52

在做信奥赛（信息学奥赛）中的for循环题目时，有一道斐波那契数列，想到的第一个方法是使用递归求解；因为以往题目最多使用的就是递归形式，但鉴于该题目在for循环题目堆，所以就思考了一些新方法；下面是我的一些思考，因为在以前从没想到过该方法，所以就在此记录下来。
参考来源君义_noip

斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……；这个数列从第3项开始，每一项都等于前两项之和。

常规求法【递归】

#include<iostream>
using namespace std;
//  斐波那契额数列函数
// n=1和n=2情况下都输出1
// 其他情况下都调用自身方法
int fb(int n)
{
	if(n == 1 || n == 2)
		return 1;
	else
		return fb(n-1) + fb(n-2);
}
// 主函数
int main()
{
	int n;
	cin>>n;
	cout<<fb(n);
	return 0;
}

上述方法易理解，代码易读；但时间复杂度高，会产生大量无用代码

新思考【还是基于递归思想，但不是递归实现】

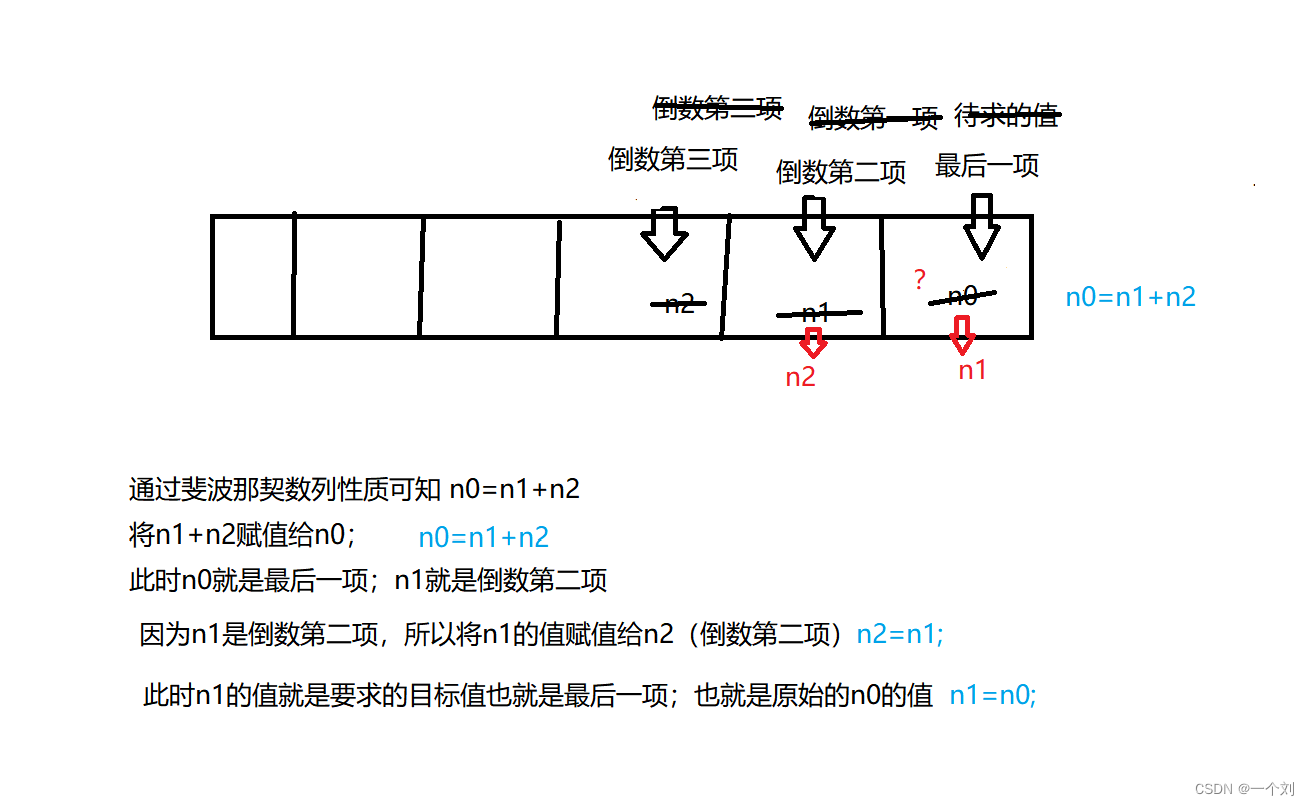
设置变量n1，n2，表示当前已知的倒数第二项，和最后一项
求新的项t，t = n1 + n2;
新的倒数第二项是原来的最后一项，所以使n2 = n1;
t将会是新的最后一项，有n1 = t;
i为3时求出第3项，i为4时求出第4项，i为k时求出第k项。循环i从3循环到k，即可求出第k项

上面是简述版，可以看懂就不需要看下面的详解了

详解

因为要求某个斐波那契数列位置上的值，只需求它前两位两个值的和即可

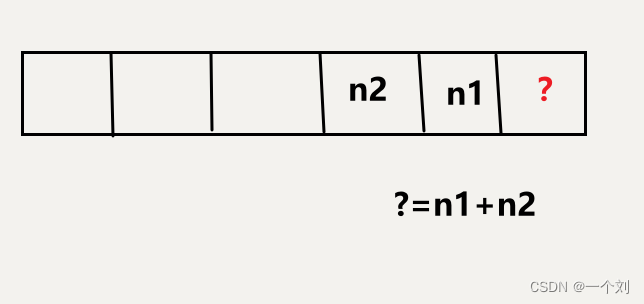
在这里插入图片描述
那我们可以设已知的最后一位值设为n1；已知的倒数第二位的值设为n2；待求的值设为n0；

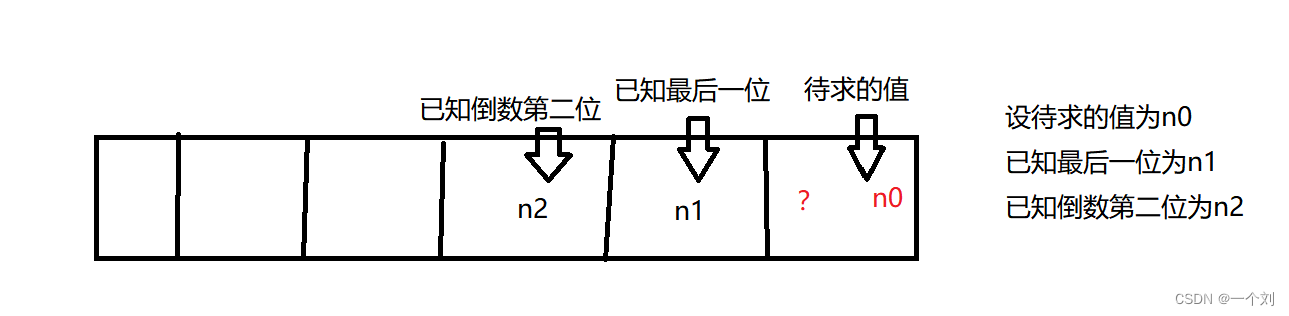
看不懂的尽量自己拿笔和本画个图就明白了

代码实现

#include<iostream>
using namespace std;
int main()
{
// n为要求第几位的值  n2为已知倒数第二项  n1为已知倒数第一项  n0为要求的那个值
	int n, n2 = 1, n1 = 1, n0;
	cin>>n;//n:第几项
	if(n <= 2)//前两项值为1
        cout<<1;
    else
    {
        for(int i = 3; i <= n; ++i)
        {
            n0 = n1 + n2;
            n2 = n1;
            n1 = n0;
        }
        cout<<n1;//输出当前求出的最后一项
    }
	return 0;
}