并查集

并查集就是对集合的合并和查询操作的统称。他要求参与运算的两个集合是不相交的(不含有相同的元素)。针对这两个集合可以进行的操作：
1.合并：将两个集合合并成一个集合。
2.查询：查询给定的两个元素是不是在同一个集合中。

并查集的表示方法

每一个并查集都使用一个树来表示，数的根用来标识整个集合，也就是说：判断两个元素是不是在同一个集合，就是看它们是不是有相同的根。
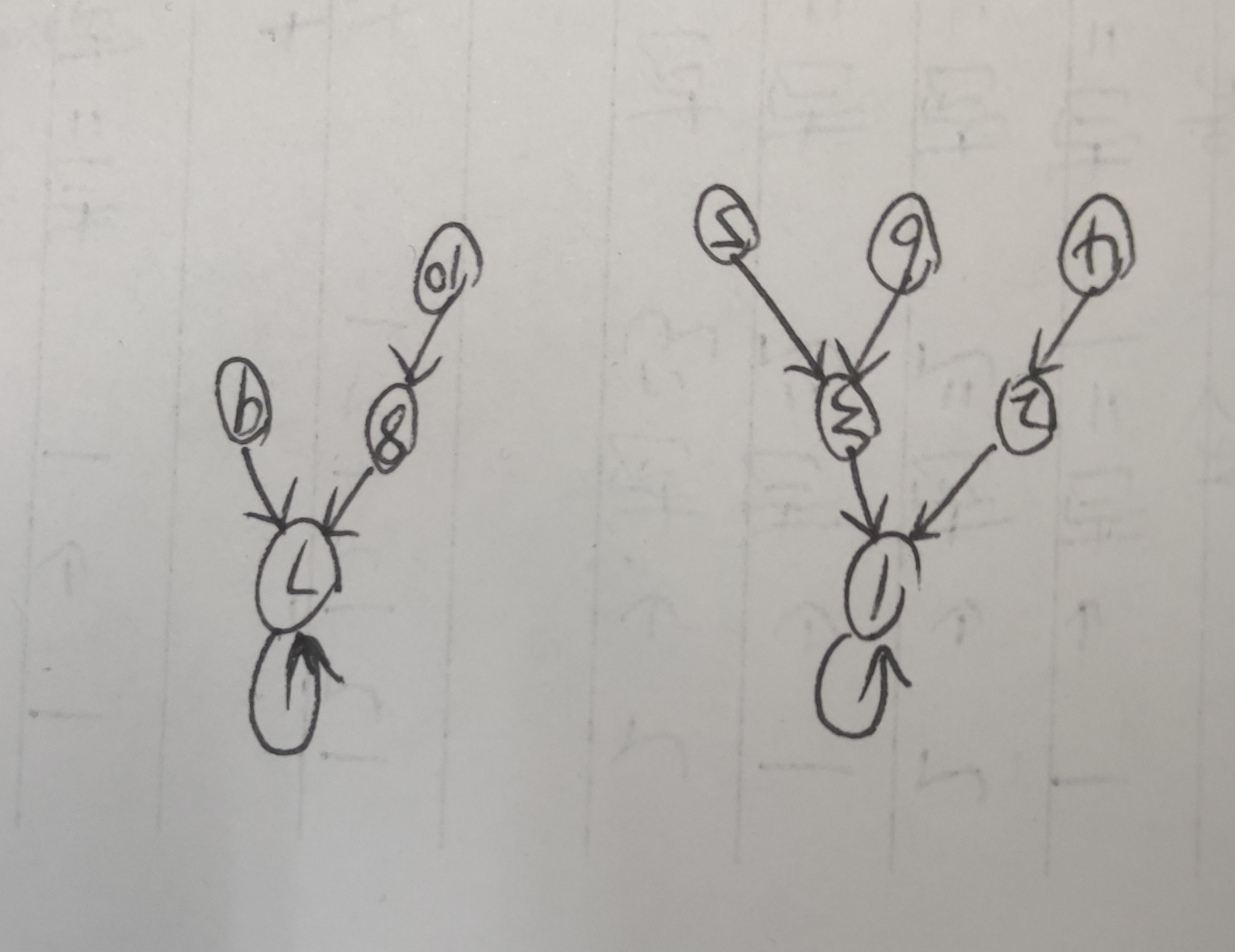
在这里插入图片描述

3和5有相同的根，它们属于同一个集合；3和7的根不同，它们属于不同的集合。
1和7的的根就是它们本身，也就是说判断一个集合的根的方法：就是找到一个节点，它的根就是它自己，那这个节点就是集合的根。

题目

给定一个长度为 N 的数组 A=[A 1,A 2 ,⋅⋅⋅,A N]，数组中有可能有重复出现的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改A 2,A 3 ,⋅⋅⋅,A N 。当修改 A i 时，小明会检查 A i是否在 A 1 ∼ A i−1 中出现过。如果出现过，则小明会给 A i 加上 1 ；如果新的 A i仍在之前出现过，小明会持续给 A i 加 1 ，直到 A i没有在 A 1 ∼ A i −1 中出现过。当 A N也经过上述修改之后，显然 A 数组中就没有重复的整数了。现在给定初始的 A 数组，请你计算出最终的 A 数组。

输入描述

在这里插入图片描述

输入示例

5
2 1 1 3 4

输出示例

2 1 3 4 5

解题思路

那这一题如何使用并查集呢？
我们要通过一定的手段让所有的根节点(假设为a)都不能在A 1 ∼ A i −1 中出现，如果根节点在A 1 ∼ A i −1 中出现了，就要更改集合的根节点a为a+1的根节点。
如何判断一个数在A 1 ∼ A i −1 是已经出现过了呢？如果它是一个集合的根节点，那么它就没有在A 1 ∼ A i −1 出现过。此时就可以将它输出。如果它不是一个集合的根节点，那么就将它所在的集合的根节点a输出，同时需要将a的根节点更改为a+1。
有如下的例子：
在这里插入图片描述
但是此时存在一个问题：根节点是8的那个树实在是太深了，这会严重拖慢访问的速度。此时就需要进行路径压缩，类似于这样：

在这里插入图片描述

压缩路径之后变成：
在这里插入图片描述

但是在压缩路径的同时也在消耗时间，为了能够最大程度的节约时间，最优的做法是一边找根节点一边进行路径压缩，具体代码是：

#一边找根节点一边进行路径压缩的代码
def findRootAndZip(x):
	# 找到x的根节点
	if(x != root[x]): # root用于存储根节点，root[x]代表x的根节点
		# 如果x的根节点和x不相同，(因为只有根节点才满足它的根节点就是它自己)
		root[x] = findFaAndZip(root[x])
	return root[x]

根据上面的分析可以写出完成代码：

N = int(input())
numList = list(map(int,input().split()))
root = [i for i in range(100005)] # 存储根节点，刚开始i的根节点就是它自己

def findRootAndZip(x):
    # 发现根节点并且进行路径压缩的函数
    if(x!=root[x]):# 如果x和root[x]不相同了,说明root存储的不在是根节点了，而是父结点
        # 如果x的根节点和x不相同，x的根节点就是x的父结点的根节点
        root[x] = findRootAndZip(root[x])
    return root[x]



for i in range(N):
    a = numList[i]
    # 直接把a的根节点打印输出
    rot = findRootAndZip(a)
    print(rot,end=' ')
    # 同时a的根节点rot变成rot+1
    root[rot] = root[rot]+1