【JAVA】双向链表详解
- 双向链表的定义
- 双向链表的初步实现(准备)
- 双向链表的操作
- 一. 打印链表
- 二. 得到链表长度
- 三. 插入操作
- 3.1 头插法
- 3.2 尾插法
- 3.3 任意位置插入
- 四. 删除操作
- 4.1 删除第一次出现为key的节点(3种情况)
- 4.2 删除所以值为key的节点(3种情况)
- 五. 清空双向链表
双向链表的定义
LinkedList的底层是双向链表结构(链表后面介绍),由于链表没有将元素存储在连续的空间中,元素存储在单独的节点中,然后通过引用将节点连接起来了,因此在在任意位置插入或者删除元素时,不需要搬移元素,效率比较高。
每个数据节点都有两个指针,指向前驱和后继,所以,双向链表中的任意一个节点开始,都可以十分方便找到前驱节点和后继节点。
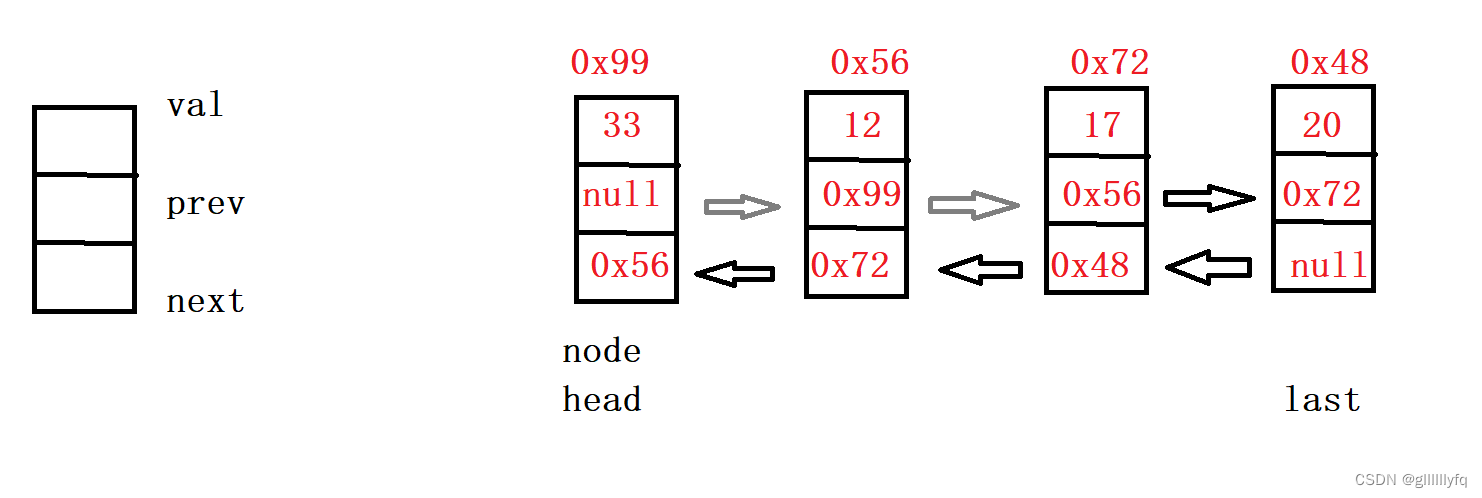
双向链表的初步实现(准备)
static class ListNode{
private int val;//值
private ListNode prev;//前驱
private ListNode next;//后继
public ListNode(int val){
this.val=val;
}
}
public ListNode head;//双向链表的头节点
public ListNode last;//双向链表的尾节点
双向链表的操作
一. 打印链表
public void display(){
ListNode cur=head;
while(cur!=null){
System.out.print(cur.val+" ");
cur=cur.next;
}
System.out.println();
}
二. 得到链表长度
public int size(){
ListNode cur=head;
int count=0;
while(cur!=null){
count++;
cur=cur.next;
}
return count;
}
三. 插入操作
3.1 头插法
当我们想把新的结点插入到第一个结点位置处,可以先建立一个结点,然后把头结点的prev变为我们新建立结点的next值,然后将我们新建立的结点值变为null,最后将头结点指向新的插入的结点。
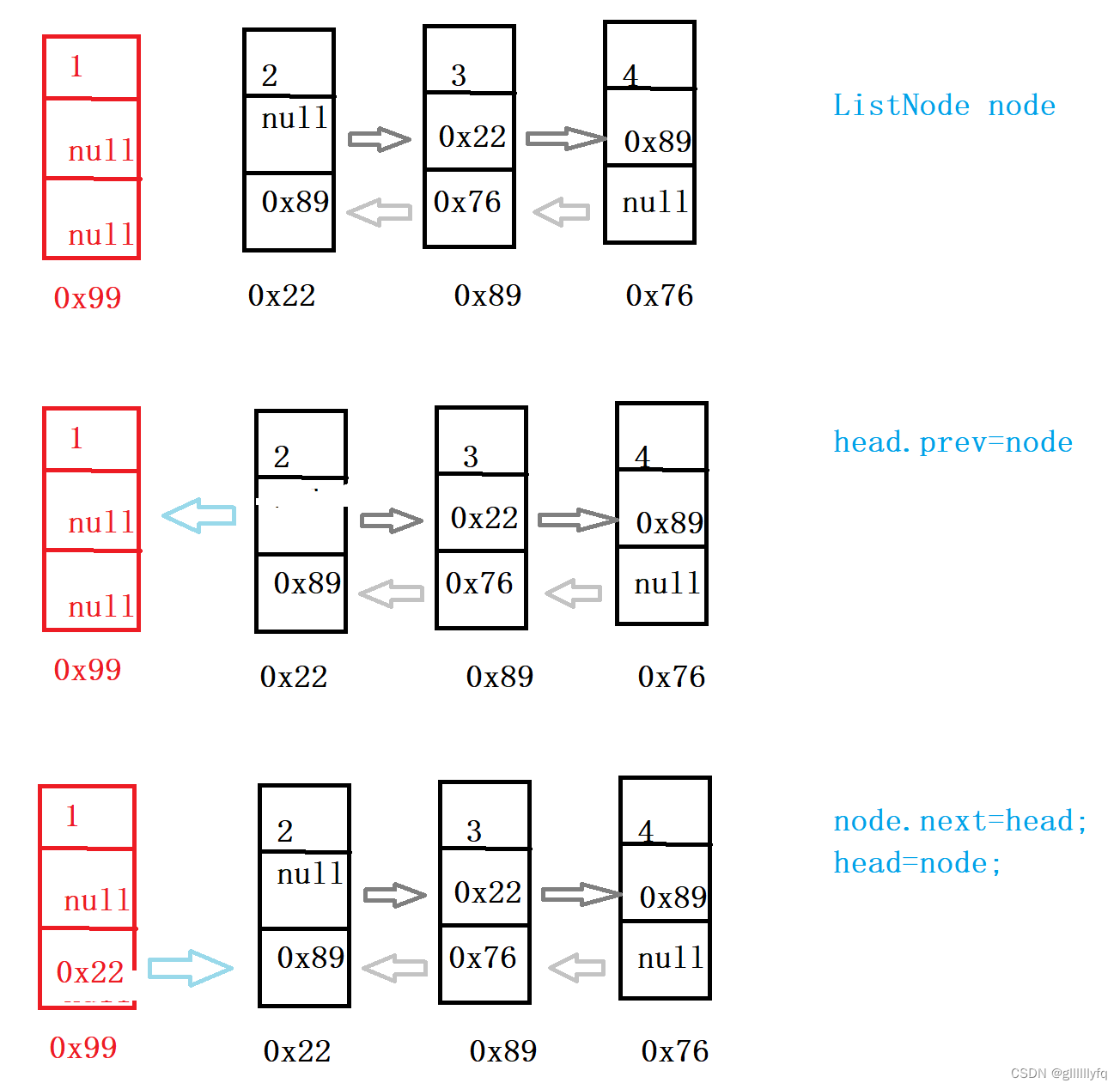
注意: 我们需要首先判断这个链表是否为空,假如为空就直接构建链表即可。
public void addFirst(int data) {
ListNode node = new ListNode(data);
//链表为空时
if (head == null) {
head = node;
last = node;
}
//有头指针,不为空
else {
node.next = head;
head.prev = node;
head = node;
}
}
3.2 尾插法
尾插法顾名思义就是从结尾插入新的结点,这个和头插法过程差不多,只不过一个是改变head的位置,一个是改变last的位置。
和头插法一样,这个同样需要判断链表是否初始为空。
public void addLast(int data){
ListNode node=new ListNode(data);
//当链表为空
if(head==null){
head=node;
last=node;
}
//有头指针,不为空
else{
last.next=node;
node.prev=last;
last=last.next;
}
}
3.3 任意位置插入
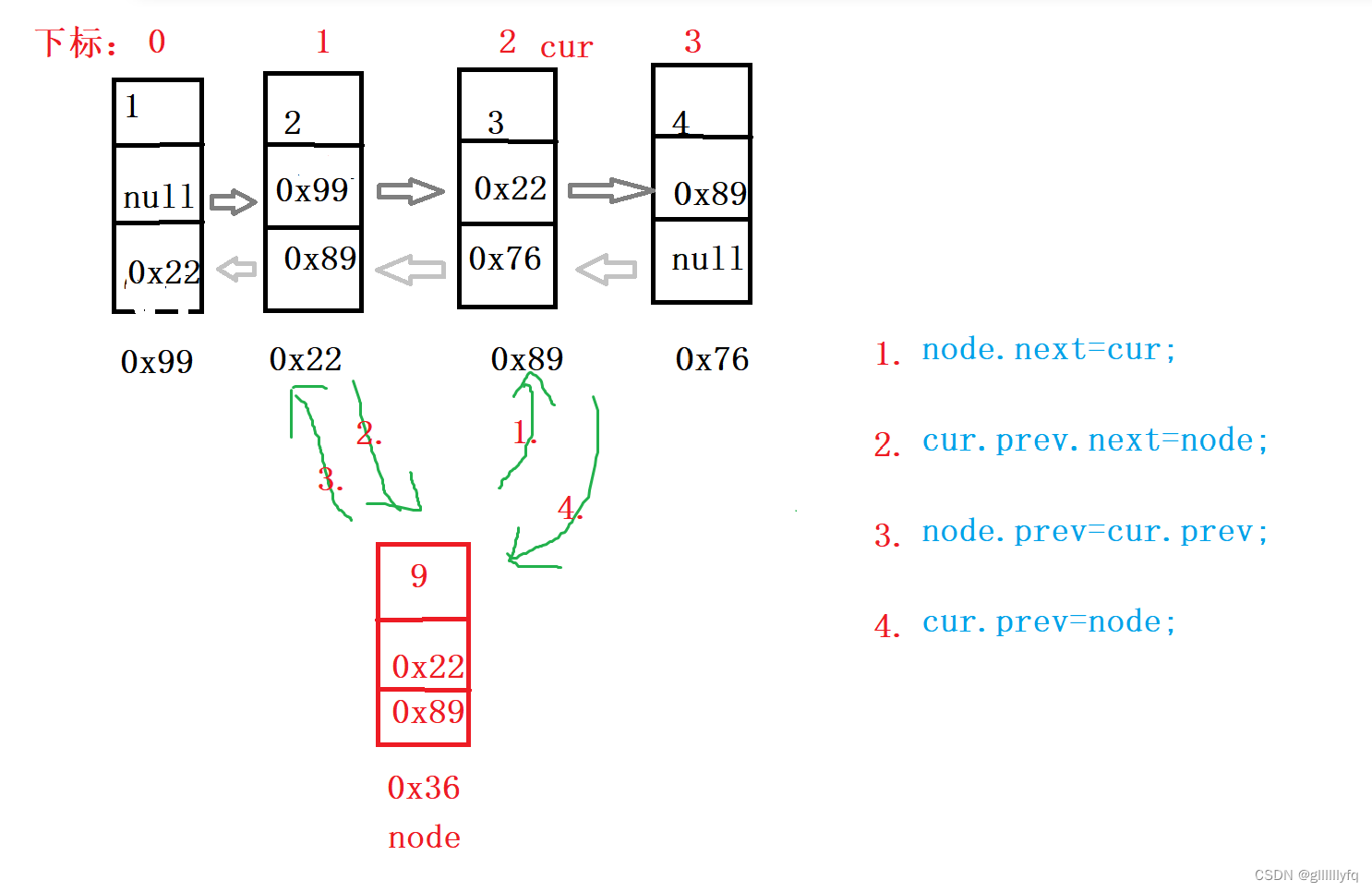
- 这个是最复杂的一种插入方式,我们需要先找到需要插入位置的结点cur,然后利用cur就可以得出前后两个结点,直接插入即可。
- 首先我们建立一个方法来查找cur的位置,一个返回值为结点的元素。
- 注意插入的先后顺序。
public void addIndex(int index,int data){
//为头插
if(index==0){
addFirst(data);
return;
}
//为尾插
if(index==size()){
addLast(data);
return;
}
//任意位置插入
ListNode cur=searchIndex(index);//找要插入的位置
ListNode node=new ListNode(data);
node.next=cur;
cur.prev.next=node;
node.prev=cur.prev;
cur.prev=node;
}
public ListNode searchIndex(int index){
ListNode cur=head;
while(index!=0){
cur=cur.next;
index--;
}
return cur;
}
四. 删除操作
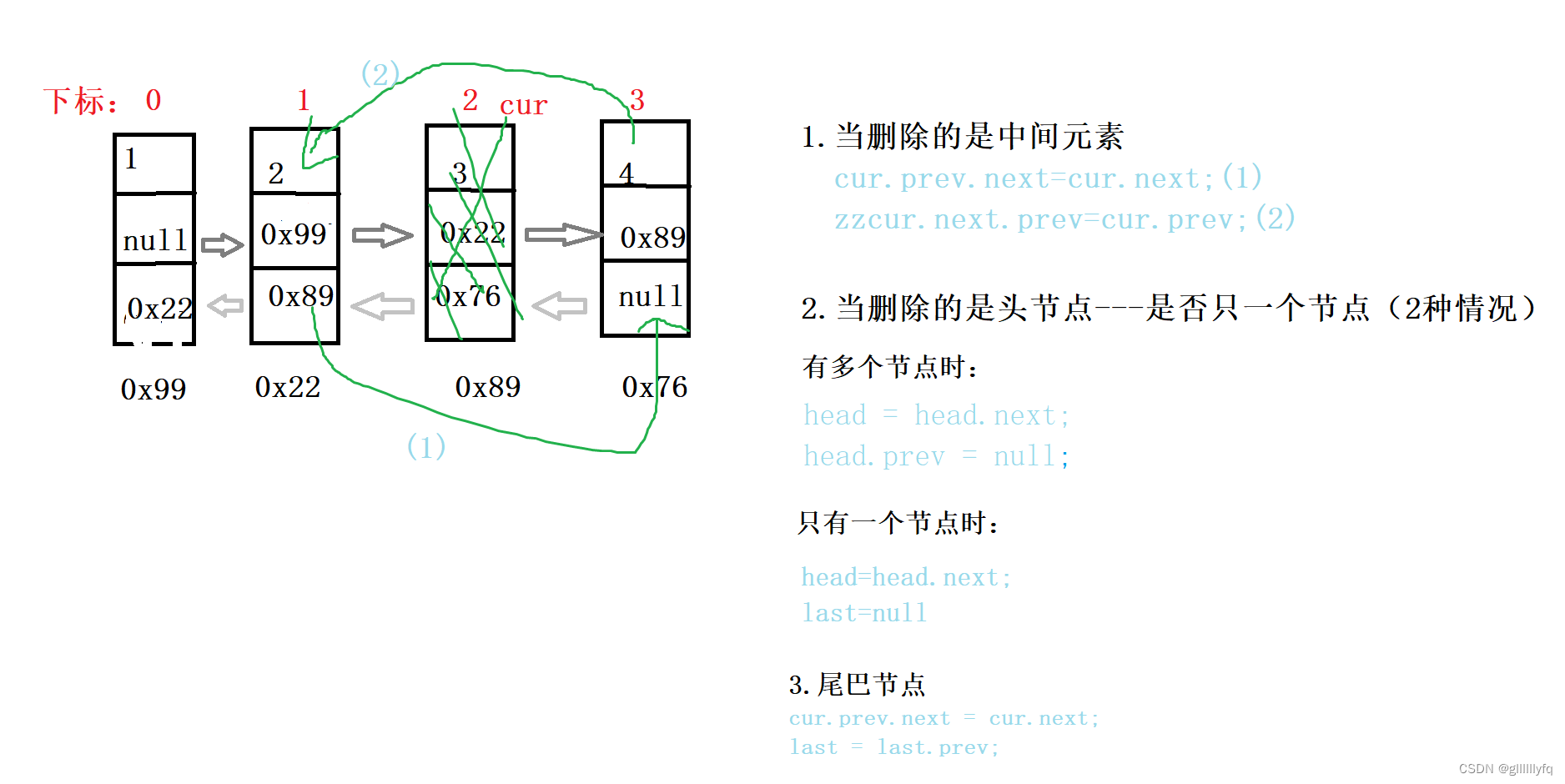
4.1 删除第一次出现为key的节点(3种情况)
假如是头结点的话我们还需要判断这个链表是否只有一个结点,如果是那么last指针也会为空,head指针也会为空,否则,我们只移动头指针结点就可以。
//删除第一次出现关键字key的节点,一共三种情况
public void remove(int key){
ListNode cur = head;
while (cur != null) {
if(cur.val == key) {
//1.当删除头节点
if(cur == head) {
head = head.next;
//1.1当头指针不为空时
if(head != null) {
//考虑只有一个节点的情况下
head.prev = null;
}else {
//1.2头指针为空时
last = null;
}
}else {
//2.删除中间节点 和 3.尾巴节点
if(cur.next != null) {
//删除中间节点
cur.prev.next = cur.next;
cur.next.prev = cur.prev;
}else {
//尾巴节点
cur.prev.next = cur.next;
last = last.prev;
}
}
return;
}else {
cur = cur.next;
}
}
}
4.2 删除所以值为key的节点(3种情况)
//删除所以值为key的节点
public void removeAllKey(int key){
ListNode cur = head;
while (cur != null) {
if(cur.val == key) {
//删除头节点
if(cur == head) {
head = head.next;
if(head != null) {
//考虑只有一个节点的情况下
head.prev = null;
}else {
last = null;
}
}else {
//删除中间节点 和 尾巴节点
if(cur.next != null) {
//删除中间节点
cur.prev.next = cur.next;
cur.next.prev = cur.prev;
}else {
//尾巴节点
cur.prev.next = cur.next;
last = last.prev;
}
}
cur=cur.next;
}else {
cur = cur.next;
}
}
}
五. 清空双向链表
public void clear(){
ListNode cur=head;
while(cur!=null){
ListNode curNext=cur.next;//保存cur.next。
cur.prev=null;
cur.next=null;
cur=curNext;
}
//最后置空
head=null;
last=null;
}
💓
感谢阅读!