今天我就不写后面的Z变换的剩下的东西了,直接写代码:
说实话,Python的Scipy.signal里面是没有和matlab一样的ztrans和iztrans,这让我头疼了几天时间,但是后面,看文档的时候,突然发现,czt是可以完成这一功能的,我们来一个很简单的z变换和z逆变换,用的也只是两个很简单的函数模块:
import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack
from scipy import signal as sign
# n=np.linspace(0,20,21,dtype= int)
n=np.array([0,1,2,3,4])
print(n)
n_ztrans=sign.czt(n)
print(n_ztrans)
n_iztrans=np.fft.ifft(n_ztrans)
print(n_iztrans.real)上述代码中,我们用signal中的czt来实现逆变换,用np.fft.ifft函数来实现z逆变换,最后我们输出z逆变换的实部就好
具体的,我实现的从matlab转换过来的都还比较少,所以这一次的代码还是比较少的,但是,在这个基础上继续实践的话,会好很多。
首先,让我们来看一个系统的频响曲线:
import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack,signal
B=np.array([1,-1.3])
A=np.array([1,0])
z,p,k=signal.tf2zpk(B,A)
w,h=signal.freqz_zpk(z,p,k,whole=True)
hf=np.abs(h)
hg=np.angle(h)
fig=plt.figure()
ax1=fig.add_subplot(1,2,1)
ax1.plot(w,hf)
ax1.grid(visible=True)
ax2=fig.add_subplot(1,2,2)
ax2.plot(w,hg)
ax2.grid(visible=True)
plt.show()这里用到的两个函数:tf2zpk,zpk2tf,再用freqz_zpk函数来计算离散时间系统的频响特性(是计算得到的h的频率、h是频率(一个复数数组)),B是分子系数,A是分母,用tf2zpk函数将信号从时域转换到z域,输出的两个数组和一个数字,其中,z是零点数组,p是极点数组,k是系统增益,这样子,我们就能够得到了离散系统幅频特性曲线ax1和拉萨系统相频特性曲线ax2(主要是用jupyter绘图的时候,汉字标题一直乱码,我就直接在后面去写了):

那么,同样的,我们再对另一个系统来绘制幅频响应和相频响应:
import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack
from scipy import signal as sign
import cmath
w=np.linspace(-4*np.pi,4*np.pi,25120,dtype= float)
x=1/(1-0.6*np.exp(-cmath.sqrt(-1)*w))
xa=np.abs(x)
xangle=np.angle(x)
fig=plt.figure()
ax1=fig.add_subplot(2,1,1)
ax1.plot(w/np.pi,xa)
ax2=fig.add_subplot(2,1,2)
ax2.plot(w/np.pi,xangle)
plt.show()
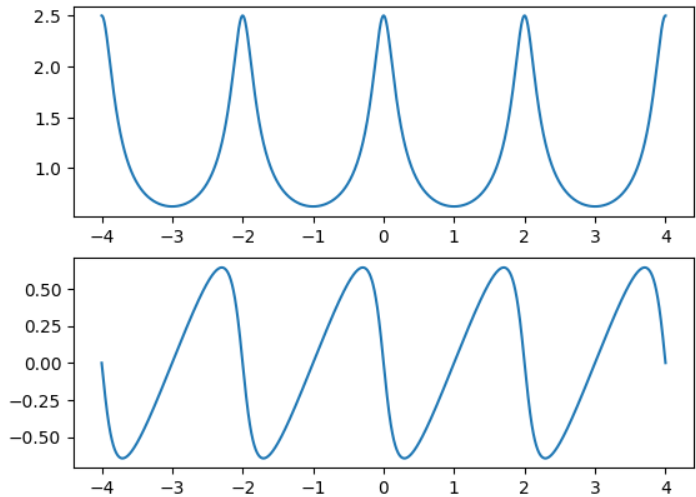
和之前的一样,第一幅图是幅频,第二幅是相频:
然后,要会画零极点图:
这里还画了单位圆,以方便我们观察,主要是对应的:
这样子的公式,那么我们就可以这样操作:
假设有个函数:
这时候,tf2zpk和zpk2tf就可以很好的发挥功效,计算零点、极点、增益,当然,这会我们还会画单位圆:
#零点分析
import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack
from scipy import signal as sign
import cmath
omega=np.linspace(0,2*np.pi,600,dtype=float)
t=np.exp(cmath.sqrt(-1)*omega)
B=[2,1]
A=[3,-1,0,0,0,1]
z,p,k=sign.tf2zpk(B,A)
absz=np.abs(z)
absp=np.abs(p)
abspmax=np.max(absp)
absk=np.abs(k)
x=max(absz,abspmax,1)
x+=0.1
y=x
xx=t.real
yy=t.imag
plt.plot(xx,yy,'blue')
plt.axis('square')
plt.plot(p.real,p.imag,'x')
plt.plot(z.real,z.imag,'o')
xlim=np.linspace(-x,x,300)
ylim=np.linspace(-y,y,300)
zlim=np.zeros(300)
plt.plot(xlim,zlim,'black')
plt.plot(zlim,ylim,'black')
plt.axis([-x,x,-y,y])
plt.title("zero and pole ")
plt.text(0.1,1.0,'Imag(z)')
plt.text(1.0,-0.1,'Real(z)')
plt.grid(visible=True)
plt.show()我试了一下,基本上没有问题,当x的size<=1的时候,这个方法,会报错,解决的方法也很简单:
# absp=np.abs(p)
# abspmax=np.max(absp)
#absk=np.abs(k)
# x=max(absz,abspmax,1)
x=1注释掉上面这些,然后让x=1就好,这样我们就可以得到系统响应的零极点图:

我本来想着把书后练习题给贴几个,但是想了想,没啥用,就没有再贴,但是原理大同小异,没什么新奇的地方。
随后我们来看一下,两个系统差分方程的单位脉冲:
import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack
from scipy import signal as sign
def filter_matlab(b,a,x):
y = []
y.append(b[0] * x[0])
for i in range(1,len(x)):
y.append(0)
for j in range(len(b)):
if i >= j :
y[i] = y[i] + b[j] * x[i - j ]
j += 1
for l in range(len(b)-1 ):
if i >l:
y[i] = (y[i] - a[l+1] * y[i -l-1])
l += 1
i += 1
return y
p=[1,-1,0]
q=[1,0.75,0.125]
x_delta=np.zeros(32)
x_delta[0]=1
h_delta=filter_matlab(p,q,x_delta)
fig=plt.figure()
ax1=fig.add_subplot(2,1,1)
ax1.stem(np.linspace(0,31,32,dtype=int),h_delta)
x1=np.ones(32)
h_unit=filter_matlab(p,q,x_delta)
ax2=fig.add_subplot(2,1,2)
ax2.stem(np.linspace(0,31,32,dtype=int),h_unit)
ax1.grid(visible=True)
ax2.grid(visible=True)
ax1.set_title("function 1 using Unit impulse response")
ax2.set_title("function using Unit step response")
plt.show()需要注意的地方是,因为Python没有filter函数的,所以我再网上找了一份filter_matlab函数来进行实现,可以得到下面这样子的结果:
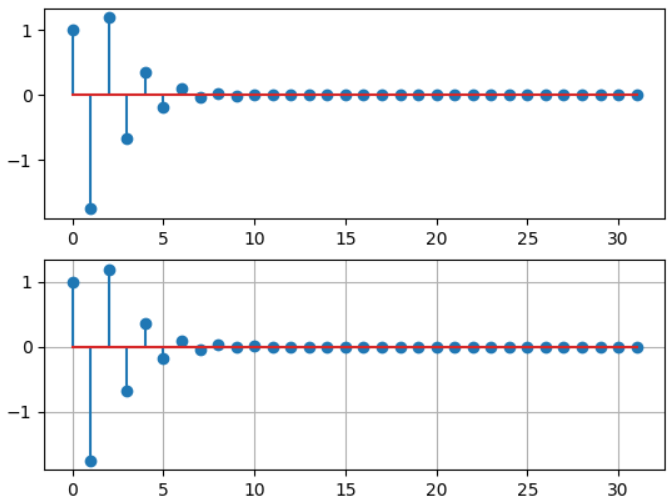
好了,z变换这两天就搞了这么多,主要两个原因:1、因为师兄给我说,我们用不上z变换,简简单单的傅里叶变换就够了,2、我自学,也没有看网课,存留了很多问题待解决,基本上是理论还没怎么通顺,所以,z变换在此也不再过多赘述,如果有需要,或者对我的代码有疑义的,可以留言大家一起解决啊!