许多问题可以用沿图的边前进所形成的通路来建模。

例如，判定能否在两个计算机之间用中间连接传递消息的问题，就可以用图模型来研究。利用图模型中的通路可以解决投递邮件、收取垃圾以及计算机网络诊断等有效规划路线的问题。

1. 通路

通路（path）是边的序列，它从图的一个顶点开始沿着图中的边行经图中相邻的顶点。

1.1 通路

通路的定义：设 n 是非负整数且G是无向图。在G中从 u 到 v 的长度为 n 的通路是G的n条边e₁, e₂, …, e_n 的序列，其中存在 x₀ = u, x₁, x₂, …, x_n = v 的顶点序列，使得对于i= 1, 2,…, n, ei 以 xi-1 和 xi 作为端点。当这个图是简单图时，就用顶点序列 x₀ , x₁ , …, x_n 表示这条通路（因为列出这些顶点就唯一地确定了通路）。

注意：长度为 0 的通路由单个顶点组成。

1.2 回路

回路(circuit）的定义：若一条通路在相同的顶点开始和结束，即 u=v 且长度大于0，则它是一条回路。（相同的顶点开始和结束且长度大于0的通路 👉 回路 / 圈）

把通路或是回路说成是经过顶点x₁, …, x_n-1 或遍历边 e₁, e₂, …, e_n 。

若通路或回路不重复地包含相同的边，则它是简单的。

1.3 其他术语

关于上面的概念，有许多不同的术语：有时使用路径（walk）而不是通路（path）,这时使用顶点和边相互交替的序列来表示 v₀, e₁, v₁, e₂, v_2,……, v_n-1, e_n, v_n

当使用 “路径（walk）” 这个术语时，就会使用 闭合路径（closed walk） 而不是 “回路” 表示起始和终止于同一顶点的路径~

使用 路线trail 表示没有重复边的路径。
通路path 常用来表示没有重复顶点的路线。

各种术语比较混乱，需要考虑上下文才能弄清楚。

2. 无向图的连通性

2.1 无向图的连通与不连通

定义：若无向图中每一对不同的顶点之间都有通路，则该图称为连通的。

不连通的无向图称为不连通的。当从图中删除顶点或边，或两者时，得到了不连通的子图。就称将图变成不连通的。
连通性满足等价关系！！！

例题：

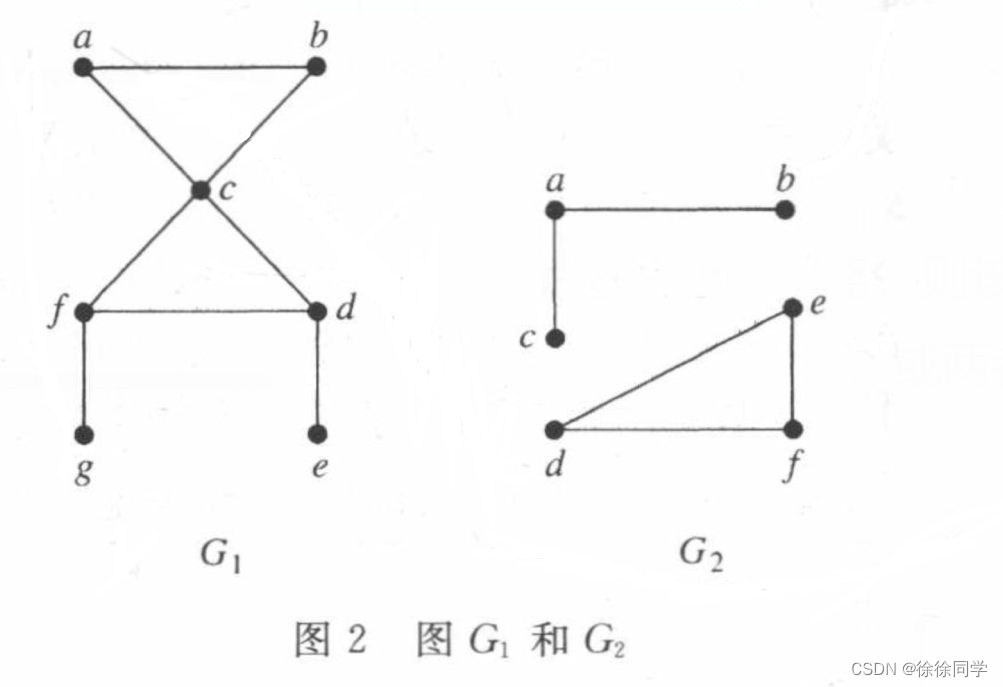
图二中，G₁是连通的，G₂是不连通的。
例如： G₂在顶点 a 和 d 之间没有通路。

2.2 定理

在连通无向图的每一对不同的顶点之间都存在简单通路

（简单通路：是通路 且 不重复地包含相同的边）

2.3 连通分支

图G的连通分支是G的连通子图，且该子图不是图G的另一个连通子图的真子图。

💙连通子图 指的是图H的一个子图H₁，且该子图H₁是连通的

图G的连通分支是G的一个极大连通子图。图G的连通分支数记作W(G)。

不连通的图G具有2个或2个以上不相交的连通子图，并且G是这些连通子图的并。

例题：
图三中H的连通分支是什么？

🔴解：图三中，图H是三个不相交的连通子图H₁、H₂、H₃的并(∪) 。这三个子图就是H的连通分支

3. 图是如何连通的

3.1 割点（= 关节点）

点割集定义： 设无向图G =（V, E）为连通图，若有点集 V₁ ⊂ V，使图G删除了 V₁ 的所有结点后，所得的子图是不连通图，而删除了 V₁ 的任何真子集后，所得到的子图仍是连通图，则称 V₁ 是G的一个点割集。

割点定义： 若某一个结点构成一个点割集，则称该结点为割点（关节点）。

3.2 割边（= 桥）

边割集定义： 设无向图 G =（V, E）为连通图，若有边集 E₁⊂E，使图G删除了E₁的所有边后，所得的子图是不连通图，而删除了E₁的任一真子集后，所得到的子图仍是连通图，则称E₁是G的一个边割集。

割边定义： 若某一个边构成一个边割集，则称该边为割边 (桥)。

3.3 不可分割图

不可分割图定义： 不含割点的连通图称为不可分割图。

不可分割图比有割点的连通图具有更好的连通性

3.4 𝑘(𝐺)

除完全图以外，每一个连通图都有一个点割集！

我们定义非完全图的点连通度为点割集中最小的顶点数，记作：𝑘(𝐺)

即：至少在连通图中删去𝑘(𝐺)个点使其不连通！

另外， 𝑘(𝐺)越大，我们认为G的连通性越好。不连通的图和K ₁
(只有一个顶点的完全图)，有 𝑘(𝐺) = 0；含有点割集的连通图和K ₂ , 𝑘(𝐺) = 2

3.5 𝑘连通的

若𝑘(𝐺) ≥ m，我们称图为m连通的（或是：m顶点-连通的）

3.6 𝑘(𝐺) ≤ λ(𝐺) ≤ δ(𝐺)

δ(G)=min {deg(v) | v ϵ V }，

连通度 𝑘(𝐺) 是为了产生一个不连通图需要删去的点的最少数目。于是一个不连通图的连通度等于0. 例如， 𝑘(K𝑝)=p-1。

定义 λ(𝐺)=𝑚𝑖𝑛{ |E₁| | E₁是G的边割集} 为G的边连通度。边连通度是为了产生一个不连通图需要删去的边的最少数目

定理：对于任何一个图G，有 𝑘(𝐺) ≤ λ(𝐺) ≤ δ(𝐺)