论文阅读:Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
今天学习的论文是 ICCV 2021 的 best paper,Swin Transformer,可以说是 transformer 在 CV 领域的一篇里程碑式的工作。文章的标题是一种基于移动窗口的层级 vision transformer。文章的作者都来自微软亚研院。
Abstract
文章的作者在摘要一开始就说他们提出了一种新的 vision transformer,叫做 swin transformer,能够作为视觉任务的通用骨干网络。然后作者说将 transformer 从 NLP 领域迁移到视觉领域的时候,因为两个领域之间的诸多差异,所以面临很多的挑战。一个是分辨率上的差异所带来的,因为视觉一般需要处理的都是图像,图像的分辨率比起文本来说维度要高很多。另外一个是物体尺度的差异,同一类物体在一张图片里面,可能尺度差异会很大,但是对于 NLP 来说,同一类物体是用文本表示,所以不存在尺度的差异。为了解决这些问题,文章作者提出了一种层级的 transformer,特征表达是通过移动窗口来进行计算,这种移动窗口的机制,不仅提升了 self-attention 的运算效率,因为 self-attention 就是在窗口内进行计算的,而且也让不同窗口之间可以产生交互。这种层级架构可以非常灵活地建模不同尺度,同时随着图像尺度的增大,其算法复杂度是线性增长的。然后文章作者列举了 swin transformer 在各种 CV 任务上的表现,包括图像的分类,图像的检测,分割等,相比之前的 sota 都有很大的提升,显示了 swin transformer 的巨大潜力。
Introduction
引言的第一段,文章作者说在 CV 领域,基于 CNN 的架构已经统治了很长的一段时间,CNN 在各种视觉任务上都是主流的 backbone。
引言的第二段,作者提到了 transformer 在 NLP 领域的成功,顺便也提到说随着 transformer 在 NLP 领域的成功,也有相关的工作尝试在 CV 任务上引入 transformer,比如 ViT。
引言的第三段是介绍这篇文章的 motivation,作者一开始就说他们希望能开发一个基于 transformer 的适合各种 CV 任务的通用 backbone。他们注意到因为 NLP 任务与 CV 任务的差异,导致了 transformer 迁移到视觉任务存在很大的挑战。一个差异就说物体的尺度,在 NLP 领域中,同一类物体可以用一个词来表示,但是在 CV 领域,同一个物体在图像中可能又不同的尺度大小,所以在某些视觉任务比如检测,分割任务,对于多尺度的建模是非常重要的。另外一个差异是图像分辨率与 Word token 之间的差异。在 NLP 领域,一个词可以用一个词表或者一个 token 来表示,这个 token 一般的长度是相对固定的,但是对于 CV 领域,输入的是图像,这个图像可以是低分辨率的,也可以是高分辨率的,这种高分辨率的图像,对 attention 的计算是非常不友好的。然后作者说,基于这两点观测到的差异,他们提出了一种针对视觉任务的通用的 transformer backbone。这种 transformer 模型可以提取多尺度的信息,同时随着图像分辨率的增加,其运算复杂度也是线性增加的。文章作者展示了图一的示意图。
从图上可以看到,swin transformer 是构建了一种层级的特征表达形式,从一开始小的 patch size 到后面逐渐增大的 patch size,将信息在不同尺度上进行抽取,这样这些多尺度的信息就可以为相应的检测或者分割任务所使用。另外,因为 swin transformer 并没有选择在整图的所有 patch 之间计算 attention,而是将整图划分成很多个 Window,然后让每个 Window 内部的 patch 之间计算自注意力。所以如果每个 Window 内的 patch 数量是固定的话,那么计算复杂度的增加主要来自于 window 数量的增加。所以作者说这种基于 window 的 attention 的计算复杂度随着图像分辨率的增加,是线性增加的。
引言的第四段,是介绍 shift window,这也是这篇文章的一个重要创新点,文章作者同样配了一张图进行说明,如图二所示:
从图二可以看到,所谓的 shift window,就是将原来的窗口往右下移动一定的距离,图二显示的移动了两个 patch 的距离,这样不同 window 之间的 patch 就可以产生交互。这样就实现了图像不同 window 之间的交互。
第五段,文章作者主要介绍了一下 swin transformer 在 CV 各个任务上的表现,基本都超越了之前的 sota。
Related Work
相关工作的第一段主要是介绍了一下 CNN 以及在视觉任务上的各种 CNN 的变体,作者列举了一些经典的网络结构。
第二段也是说因为 self-attention 以及 transformer 在 NLP 领域的成功应用,也有一些工作尝试在视觉领域引入 self attention 的机制。
第三段也是介绍了一些视觉任务如何把 self-attention 与 CNN 模型相结合的工作。
第四段主要是介绍 ViT 以及基于 ViT 之后的一些衍生工作,文章作者也提到说因为 ViT 是在全图的所有 patch 之间计算 attention,所以 ViT 处理高分辨率图像的时候,算法复杂度是平方增加的。
Method
Overall Architecture
接下来,看文章的核心部分,也就是文章的方法及模型。文章作者给整个的算法框架也配了一张流程图,如下图所示:
文章呈现的算法框架图对应的是 Swin-T 也就是 Swin transformer 的 tiny 版本。首先,拿到一张输入的 RGB 图像,然后,像 ViT 一样,先拆分成很多个 patch,在 tiny 版本里,每个 patch size 是 4 × 4 4 \times 4 4×4, 因为是三通道,所以把每个 patch 拉伸成 1-d 向量的时候,这个 patch 的维度就是 4 × 4 × 3 = 48 4 \times 4 \times 3 = 48 4×4×3=48,每个 patch 可以理解成 NLP 中的一个 token,一张图有多少个 patch,就类似有多少个 token,如果输入图像的尺寸是 224 × 224 × 3 224 \times 224 \times 3 224×224×3,那么如果每个 patch 的大小是 $ 4 \times 4 \times 3$ 的话,就会有 224 ∗ 224 / ( 4 ∗ 4 ) = 56 ∗ 56 224 * 224 / (4 * 4) = 56 * 56 224∗224/(4∗4)=56∗56 个 patch。所以示意图上的 patch partition 就是把一张 $ H \times W \times 3$ 的图,变成一个 H 4 × W 4 × 48 \frac{H}{4} \times \frac{W}{4} \times 48 4H×4W×48 的一个张量。这个张量随后会进一个 linear embedding 层,就是一个线性投影,将 48 变成一个特定维度 C 的向量。文章中 C = 96。通过 linear embedding 之后,整个张量就变成了 56 × 56 × 96 56 \times 56 \times 96 56×56×96,前面的 56 × 56 = 3136 56 \times 56 = 3136 56×56=3136 表示 patch 的数量,也就类似序列的长度,而后面的 96 表示每个 token 的向量维度。很显然,这个 3136 的序列长度,对于 transformer 来说,还是太长了。所以文章作者引入了基于 window 的 self-attention。文章中的每个窗口默认是 7 × 7 = 49 7 \times 7 = 49 7×7=49 个 patch,所以每个窗口的序列长度变成了 49, 这个序列长度对于 transformer 来说是完全可以接受的。所以框架图中的 stage-1 就是基于窗口的 self-attention 在计算,如果没有任何约束的话,transformer 的输入和输出是完全一致的,所以这里的 stage-1 的输入输出也是一致的,经过 stage-1 之后,整个张量还是 56 × 56 × 96 56 \times 56 \times 96 56×56×96。
接下来进入 stage-2 之前,有一个 patch merging,从框架的示意图来看,后面的每个 stage 做完之后,patch 的数量都在减少,但是 token 的维度在增加。所以可以大概明白 patch merging 的操作就是把每个 patch 的向量维度进行了扩展,这个扩展其实就是通过把 patch 进行 concatenate 来实现的,具体的操作如下:
- 对于一个 H × W × C H \times W \times C H×W×C 的张量,在 H 和 W 的方向上,分成若干个 2 × 2 2 \times 2 2×2 的邻域
- 每个邻域按照从左往右,从上到下的顺序进行编号 1,2,3,4
- 然后对每个邻域里编号相同 的 patch 抽取出来,并且放到一起
- 这样一个 H × W × C H \times W \times C H×W×C 的张量就会变成 4 个 $ \frac{H}{2} \times \frac{W}{2} \times C $ 的张量
- 将这 4 个张量在 C C C 的维度进行 concat,就会得到 1 个 $ \frac{H}{2} \times \frac{W}{2} \times 4C $ 的张量
- 然后对这个张量再做一个线性投影,最后就得到一个 $ \frac{H}{2} \times \frac{W}{2} \times 2C $ 的张量
所以看框架示意图,可以发现,每过一个 stage,整个张量的 patch 数量减少 4 倍,同时对应的 token 的向量维度增加一倍。文章中说这是为了和 CNN 中的一些设置相匹配,CNN 中,一般通道数增加一倍,feature map 的尺寸减少 4 倍。所以整个计算下来,我们可以给出一个具体的维度变化的过程:
- 输入: 224 × 224 × 3 224 \times 224 \times 3 224×224×3
- 通过 patch partition,得到 56 × 56 × 48 56 \times 56 \times 48 56×56×48 的张量
- stage-1,先通过 linear embeding,得到 56 × 56 × 96 56 \times 56 \times 96 56×56×96 的张量
- stage-1,再通过 swin-transformer block,同样输出一个 56 × 56 × 96 56 \times 56 \times 96 56×56×96 的张量
- stage-2,先经过一个 patch merging,输出一个 28 × 28 × 192 28 \times 28 \times 192 28×28×192 的张量
- stage-2,再通过 swin-transformer block,同样输出一个 28 × 28 × 192 28 \times 28 \times 192 28×28×192 的张量
- stage-3,先经过一个 patch merging,输出一个 14 × 14 × 384 14 \times 14 \times 384 14×14×384 的张量
- stage-3,再通过 swin-transformer block,同样输出一个 14 × 14 × 384 14 \times 14 \times 384 14×14×384 的张量
- stage-4,先经过一个 patch merging,输出一个 7 × 7 × 768 7 \times 7 \times 768 7×7×768 的张量
- stage-4,再通过 swin-transformer block,同样输出一个 7 × 7 × 768 7 \times 7 \times 768 7×7×768 的张量
所以整个过程走下来,可以看到 patch merging 就是在进行一个多尺度信息提取的操作。然后每个 stage 都可以输出不同尺度的张量,就类似 CNN 里的 feature map。
Shifted Window based Self-Attention
接下来作者介绍了本文的核心贡献,也就是基于移动窗口的 self-attention,作者已经在前面也强调过他们为什么提出这种移动窗口的 self-attention,首先基于窗口的 self-attention 是为了减小计算的复杂度。
首先一张图会被划分成若干个没有重叠的窗口,每个窗口里面都包含 $M \times M $ 个 patch,论文中是 $ 7 \times 7 = 49 $ 个 patch,如果以 stage-1 为例,进入 swin-transformer block 之前的张量维度是 56 × 56 × 96 56 \times 56 \times 96 56×56×96,每个窗口的 patch 数是 $ 7 \times 7 = 49 $,所以一共有 $ 8 \times 8 = 64$ 个窗口。作者基于这个给出了一个比较,下面的两个式子分别给出了标准的多头自注意力与基于窗口的自注意力机制的算法复杂度:
Ω ( MSA ) = 4 h w C 2 + 2 ( h w ) 2 C Ω ( W-MSA ) = 4 h w C 2 + 2 M 2 h w C \Omega(\text{MSA}) = 4hwC^{2} + 2(hw)^{2}C \\ \Omega(\text{W-MSA}) = 4hwC^{2} + 2M^{2}hwC Ω(MSA)=4hwC2+2(hw)2CΩ(W-MSA)=4hwC2+2M2hwC
可以看到基于窗口的 self-attention 的算法复杂度比起标准的多头 self attention 来说,要小很多。
接下来,文章作者介绍怎么实现基于移动窗口的 self-attention 的计算,因为窗口的划分是没有重叠的,所以每个窗口与窗口之间是不存在交互的,这样不利于对全局信息的提取,为了能让窗口与窗口之间实现交互,从而能让全局信息得到更好的提取,作者就设计了这种基于移动窗口的 self-attention 的机制。所以 swin-transformer 的算法流程,每个 swin-transformer block 里面包括两种 self-attention 的计算,一种是标准的窗口 self-attention 的计算,紧接着就是移动窗口的 self-attention 的计算。文章作者也给出了具体的公式:
然后,作者介绍了一种基于移动窗口的 self-attention 的快速计算的方式,文章作者提出了一种非常巧妙的循环移位以及掩码,使得移动窗口可以在不增加多余窗口数量的情况下,高效的并行计算。
我们先回顾一下图二的移动窗口的示意图,我们可以看到,左边是标准的窗口形式,图上展示的是 4 个窗口,右边是移动窗口的示意图,可以看到,窗口移动之后,虽然不同区域的内容得到了交互,但是窗口的大小及尺寸都发生了变化,从之前的 4 个窗口变成了 9 个窗口,而且每个窗口的 patch 数量也不一样了,这对并行计算来说非常不友好,一种方式就是对那些 patch数量不够的窗口补 0,这样无疑会增加计算量。文章作者设计了一种非常巧妙的循环移位让移动之后的窗口数量还是和之前一样,如下图所示:
从上图可以看出,当移动窗口之后,文章作者通过一种循环移位的方式,将坐标和上面的一些窗口移动到下面和右边,这样可以重新组成 2 × 2 = 4 2 \times 2 = 4 2×2=4 个窗口,然后这 4 个窗口同样可以计算 self-attention,计算完之后,再把这些窗口反移位回去,就又变成和之前一样的了。不过这里会有另外一个问题,就是循环移位之后,有些窗口里的 patch 不再是相邻的了,如果以图 4 为例,我们可以看到,做完循环移位之后,只有左上角的那个窗口里的 patch 在原图上都是相邻的,所以可以直接做 self attention,但是其它几个窗口里的 patch,在原图上的位置都是不相邻的,这些窗口里的 patch 如果还是和之前一样计算的话,这个相关性会出问题。所以作者又设计了一种很巧妙的掩码,循环移位之后,如果同一个窗口里的 patch 是不相邻的,那么计算 self attention 的时候,那些不相邻的 patch 的权重会赋予一个很大的负数,这样送入 softmax 计算权重的时候,这些不相邻的 patch 就不会产生贡献。
我们以文章中每个窗口 7 × 7 = 49 7 \times 7 = 49 7×7=49 个patch 的数量为例,如果每个窗口算 self-attention,就会得到一个 49 × 49 49 \times 49 49×49 的矩阵,这个矩阵的行,表示每个 patch 的编号,这个矩阵的列表示每个 patch 与其它 patch 之间的相似度。所以这个掩码其实也是一个 49 × 49 49 \times 49 49×49 的矩阵。
假设每个 patch 的向量维度为 C C C,那么每个窗口计算 self-attention 的时候,就是先将每个窗口的所有 patch 放到一起,变成一个 49 × C 49 \times C 49×C 的矩阵,假设这个矩阵为 A A A,那么相关性就是:
A × A T = 49 × 49 A \times A^{T} = 49 \times 49 A×AT=49×49
所以,只要看看这个 $49 \times 49 $ 的矩阵里,哪两个 patch 是来自同一个区域,哪两个 patch 是来自不同的区域,就能知道这个掩码的值到底赋多少。这里给出文章作者给出的掩码的可视化图。
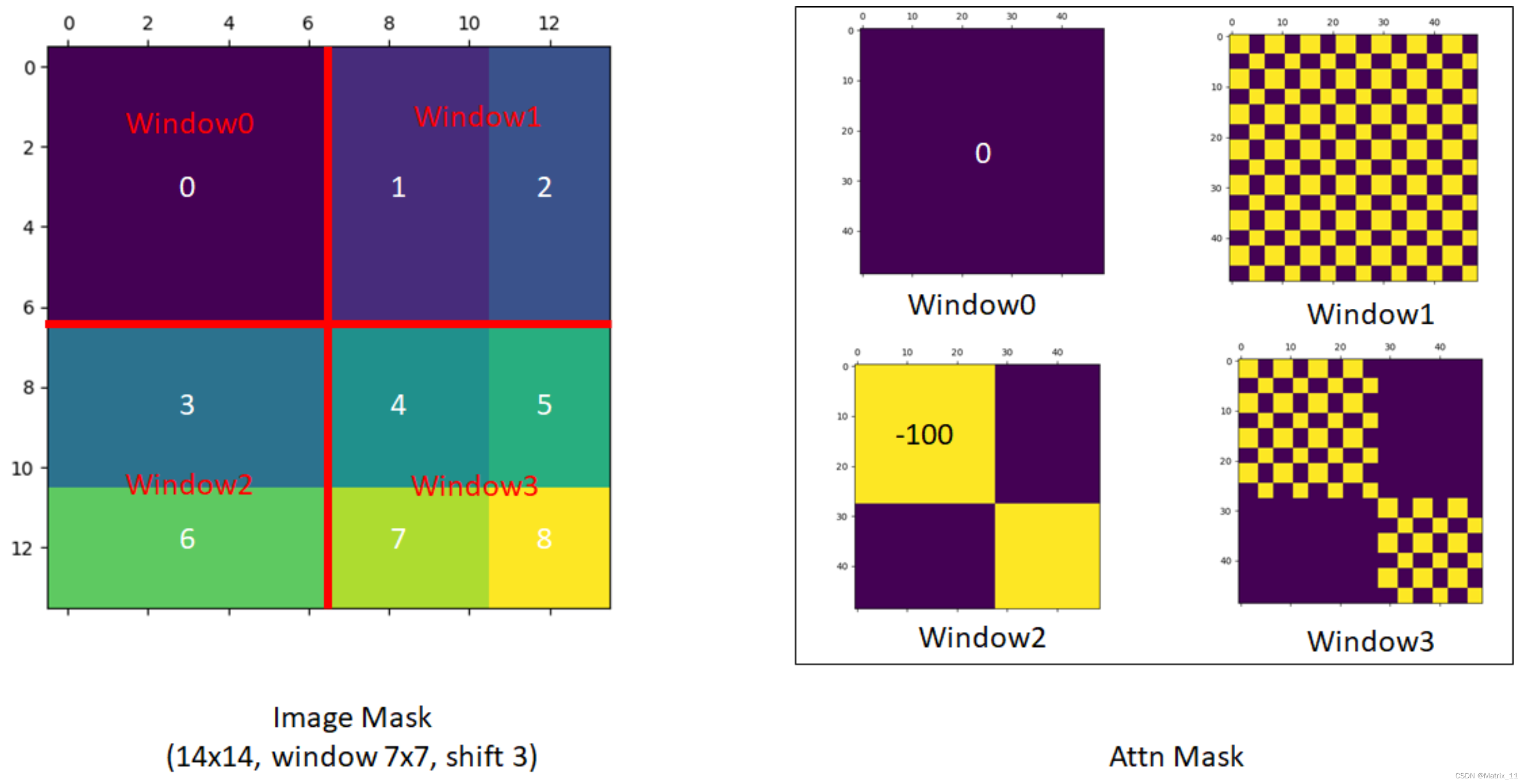
- Relative position bias,最后文章作者也介绍了一下相对位置编码,swin transformer 用的是相对位置编码,
Attention ( Q , K , V ) = Softmax ( Q K T / d + B ) V \text{Attention}(Q, K, V) = \text{Softmax} (QK^{T} / \sqrt{d} + B)V Attention(Q,K,V)=Softmax(QKT/d+B)V
其中, Q , K , V ∈ R M 2 × d Q, K, V \in R ^{M^2 \times d} Q,K,V∈RM2×d 表示一个窗口内,query,key, value 组成的矩阵, d d d 表示 query/key 的向量维度, M 2 M^{2} M2 表示一个窗口内的 patch 数量。
最后,作者给出了 swin transformer 的几种变体:
- Swin-T(tiny): C=96, layer-numbers = {2, 2, 6, 2}
- Swin-S(small): C=96, layer-numbers = {2, 2, 18, 2}
- Swin-B(base): C=128, layer-numbers = {2, 2, 18, 2}
- Swin-L(large): C=192, layer-numbers = {2, 2, 18, 2}
其中 Swin-T 的复杂度和 ResNet50 差不多,而 Swin-S 的复杂度和 ResNet101 差不多。 C C C 表示 stage-1 中的 linear-embedding 之后的向量维度。
- 参考:
https://www.bilibili.com/video/BV13L4y1475U/?spm_id_from=333.788&vd_source=bb80399e033aacf33a21a9f9864c6086