目录
- 数值数据的表示
- 一.进位计数制理解
- 1.你需要了解的概念
- 2. 晦涩难懂的官方定义
- 3 一看就会的例子
- 4 值得收藏的进制对照表(二、八、十、十六进制)
- 5 计算机为什么主要使用二进制
- 二.不同数制之间的转换
- 1. 为什么会出现进制转换
- 2. 各数制转十进制
- 3. 十进制转二进制
- 4. 二进制与八进制、十六进制之间的转换
- 三.十进制数的编码
- 1.二—十进制码(BCD码)
- 2.十进制字符串的表示方法
数值数据的表示
一.进位计数制理解
1.你需要了解的概念
所谓进位计数制即按进位制的方法进行计数。
数制的组成: 基数R和各数位的权W。
基数为R的数制称为R进制,特点逢R进一
基数R: 决定了各数位上允许出现的数码个数,比如十进制上允许出现10个数(0、1、2…9)。
权W: 表示该数位上的数码苏表示的单位数值的大小,比如十进制的个位数值大小为100,十位为101,
所以权W是与数位的位置有关的一个常数,即不同数位有不同的权。
位权: 同一个数码位于不同的位置,其所代表的数值大小也不同。
最高有效位: 通常一个数最左边的数位的权最大,即最高有效位。
最低有效位: 通常一个数最右边的数位的权最小,即最低有效位。
2. 晦涩难懂的官方定义

3 一看就会的例子

计算机中常见的数制(允许使用的数字符号)有:
二进制(0~1)
八进制(0~7)
十进制(0~9)
十六进制(0~9及 A~F)。
4 值得收藏的进制对照表(二、八、十、十六进制)

5 计算机为什么主要使用二进制
- 相对更容易找到具有二进制状态的物理器件表示数据和实现存储。例如,脉冲的有无、电压的高低等。
- 二值性使二进制数的存储具有抗干扰能力强、可靠性高等优点。
- 二进制的运算规则简单,运算过程中的输入和输出状态较少,便于使用电子器件和线路加以实现。
- 二进制的0和1与逻辑推理中的“真”和“假”相对应,为实现逻辑运算和逻辑判断提供了便利。
二.不同数制之间的转换
说明: 以下出现例子中括号外右下角以数制的基数2、10、8、16或后缀以大写或小写的“B(Binary)”、“D(Decimal)”、“O(Octal)”、“H(Hexadecimal)”代表二进制、十进制、八进制、十六进制。
1. 为什么会出现进制转换
由于人们习惯使用十进制,所以计算机中支持用户以十进制形式输入数据,在计算机内部将其转化为二进制数来存储和运算,最后再将处理结果以十进制形式输出给用户。
2. 各数制转十进制
给我死死的记住:计算的本质——加权求和!

3. 十进制转二进制
十进制的整数部分和小数部分必须分别转换,得出结果再合并。
- 整数转二进制: 除以2取余数,先得者为整数的最低位,再继续除以2取余数,直至商为0.
- 小数转二进制: 乘以2取整数,先得者为小数的最高位。再继续乘以2取整数,直至积为0或小数满足精度要求(并不是所有十进制小数最后乘积一定为0,所以适当使用精度控制结束)。
一个例子你就懂:
将(114.35)10 转化为二进制(1110010.0101)2,精度高于10%(因为1/16<1/10=10%,即取4位小数即可)。

4. 二进制与八进制、十六进制之间的转换
- 二进制转八进制
因为3位二进制数恰好组成1位八进制数,所以从小数点开始向两边每3位划分为一组,整数部分不足3位的,在前边补“0”,小数部分不足3位的在后边补“0”,然后写出各组的八进制数。 - 二进制转十六进制
同理4位二进制组成1位十六进制数,所以从小数点开始向两边每4位划分为一组,整数部分不足4位的,在前边补“0”,小数部分不足4位的在后边补“0”,然后写出各组的十六进制符号。 - 八进制转二进制
对每一位八进制写出它的3位二进制编码(注意:不能省略高位或低位的“0”,当整个过程转换完成时,才可以省略高位或低位的“0”) - 十六进制转二进制
同八进制转二进制思路一样,对每一位十六进制写出它的4位二进制编码。
例1:将(11011.11001)2转化为八进制和十六进制

例2:将(571.23)8和(A8.E9)16转化为二进制

三.十进制数的编码
由来: 人们习惯使用十进制表示数据,而计算机内任何信息只能以二进制存储,如何使用二进制表示十进制?达到快速转换即像查表一样一一对应?
以下两种方法表示: BCD码和十进制数串的表示方法
1.二—十进制码(BCD码)
BCD(Binary Coded Decimal)码,即使用二进来编码十进制数0~9。
通常使用4位二进制编码来表示1位十进制,选16个4位二进制编码中的10个来表示数字0~9。不同选择构成不同的BCD码。
如下表:BCD码编码对应关系

如下图为对BCD码的总结:
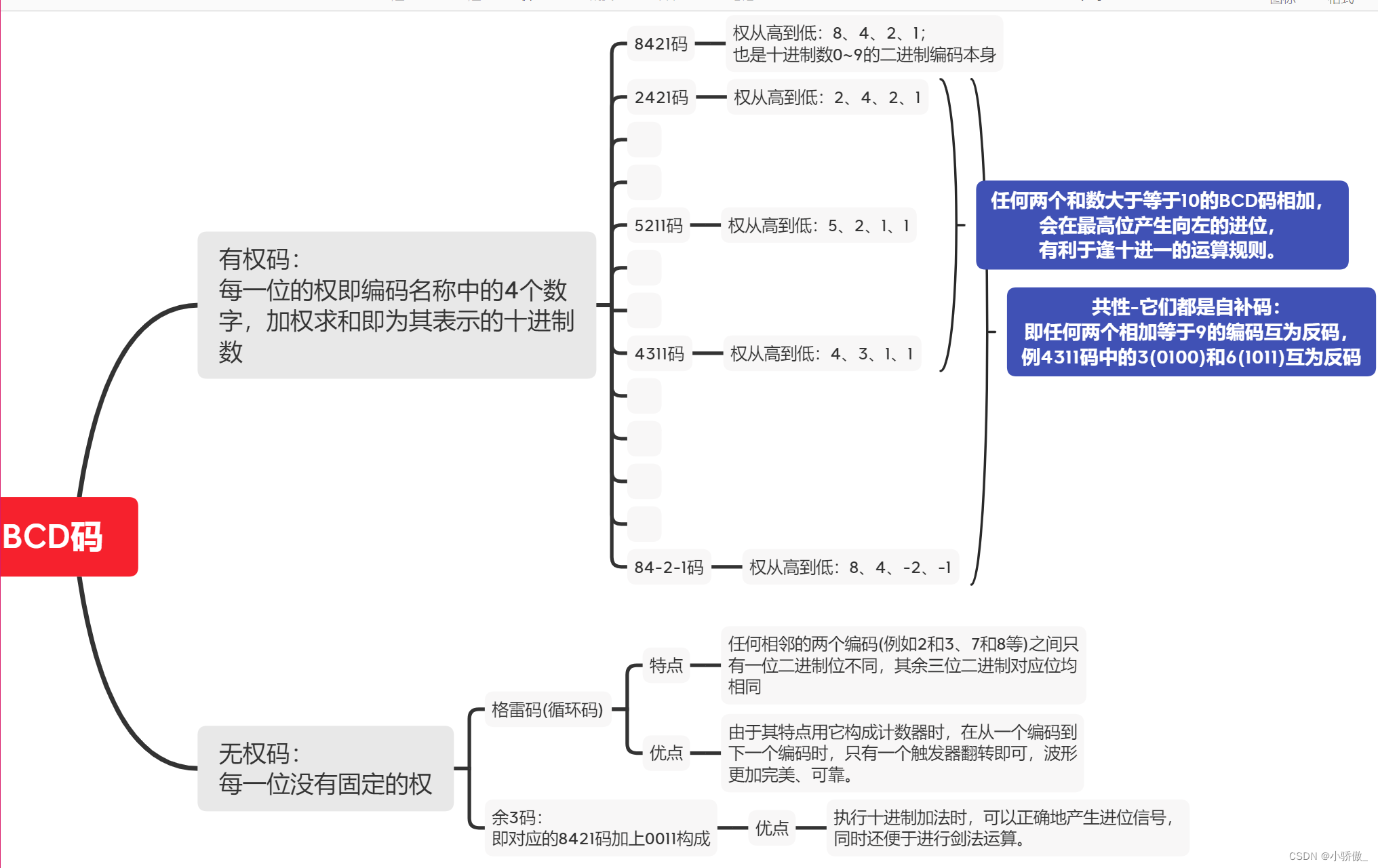
额外补充: