目录
1. INTRODUCTION TO SEPARATION LOGIC 分离逻辑
1.1 霍尔推理(Hoare Reasoning)
1.2 堆指针的影响
1.3 全局和局部推理(Global and Local Reasoning)
1.4 组合推理(Compositional Reasoning)
1.5 The Frame Rule
1.6 The Side Condition
1.7 Validity of Triples 三元组的有效性
1.8 Memory Safety 内存安全性
2. A LITTLE MORE FORMALLY
2.1 Expressions, Commands
2.2 Heap Read Rule (Simplified)
2.3 Assignment Rules
2.4 Frame Rule
2.5 Example Proof
编辑
2.6 Inductive Predicates
2.7 Example: Tail
1. INTRODUCTION TO SEPARATION LOGIC 分离逻辑
1.1 霍尔推理(Hoare Reasoning)

霍尔推理是一种用于推理程序正确性的形式化方法,其主要组成部分是霍尔三元组(Hoare Triple):{P} prog {Q},表示在前置条件P成立的情况下,执行程序prog,之后后置条件Q会成立。对于局部变量x和y,这种推理方式在x和y不相互引用(即不能为别名)的情况下才有效。
-
赋值规则(ASSIGN):{Q[e/x]} x := e {Q},这个规则表示,如果在赋值后的状态Q中将x替换为表达式e可以得到前置状态,那么这个霍尔三元组是有效的。
-
顺序规则(CONSEQ):(P → P’ {P’} prog {Q’} Q’ → Q) / ({P} prog {Q}),这个规则表示,如果从前置条件P可以推导出另一个前置条件P’,并且从后置条件Q’可以推导出另一个后置条件Q,那么原本的霍尔三元组的效果可以通过新的三元组来实现。
这两个规则在处理基本赋值语句和逻辑推导时十分有用。但是,它们在处理指针和别名等更复杂的数据结构时会变得不够用。
1.2 堆指针的影响

在处理像 *x := 2 这样的语句时,我们需要引入一种新的断言,称为映射断言(Maps-To Assertion):p ↦ e,表示通过p识别的堆位置保存了值e。但这并不能完全解决问题,因为当x和y指向同一个位置,也就是别名的情况时,这个霍尔三元组就会失效。因此,我们需要一种能够处理别名情况的方法。
1.3 全局和局部推理(Global and Local Reasoning)
在霍尔逻辑中,谓词P和Q都是对全局状态进行描述的。这在处理全局变量或者独立的局部变量时没有问题,但是在处理像堆这样的共享结构时就会变得复杂。
为了解决这个问题,分离逻辑引入了一种新的想法:谓词P只描述它关心的状态部分,这部分被称为谓词的领域(也叫足迹),记作 dom(P)。对于映射断言 p ↦ e,它的领域就是{p}。

![]()

1.4 组合推理(Compositional Reasoning)

分离逻辑引入了一种新的连接符:分离连词 P ⋆ Q,表示P和Q各自描述了各自的状态部分,并且这两部分是分离的。这就为处理别名问题提供了一种手段。在 P ⋆ Q 中,如果 P 和 Q 有共同的领域,那么 P ⋆ Q 就无法成立。这可以用来表达 x 和 y 不可能是别名的情况。

1.5 The Frame Rule

分离逻辑的一个重要理论是帧规则(FRAME Rule):({P} prog {Q} modv(prog) ∩ fv(R) = {}) / ({P ⋆ R} prog {Q ⋆ R})。这个规则的意思是,如果一个程序没有修改R中的任何变量,那么就可以从{P} prog {Q}推导出{P ⋆ R} prog {Q ⋆ R}。也就是说,如果我们知道在P的情况下执行prog可以得到Q,那么在P和R同时成立的情况下执行prog,我们不仅可以得到Q,还可以得到R。
1.6 The Side Condition

在上述帧规则中,有一个旁注条件:程序修改的变量集合和R中的自由变量集合不相交。如果这个条件不成立,那么我们就无法保证R在程序执行后仍然成立。
1.7 Validity of Triples 三元组的有效性

在分离逻辑中,霍尔三元组{P} prog {Q}的含义是部分正确性(Partial Correctness):如果P在程序开始时成立,那么只要程序正常终止,Q就会成立,而且,程序绝对不会出错。
1.8 Memory Safety 内存安全性

在一个所有内存不安全访问都会导致失败的语言语义中,分离逻辑可以保证内存安全。比如访问一个未初始化的指针这样的情况,在分离逻辑中是不被允许的。
2. A LITTLE MORE FORMALLY
2.1 Expressions, Commands

表达式 (e) 是指可以由变量 (x) 或数字 (n) 组成的。它可以提及局部变量,但不能提及堆。表达式在一个存储 s 中求值,其中 s 是一个函数,将变量映射到整数上。
命令 (c) 是构造程序的基本元素。以下是一些基本的命令类型:
- c1 ; c2:命令序列,首先执行c1,然后执行c2。
- if e then ct else cf:条件语句,如果表达式 e 为真,则执行 ct,否则执行 cf。
- while e do c:循环语句,只要表达式 e 为真,就执行命令 c。
- x := e:将表达式 e 的值赋给变量 x。
- x := *e:将地址 e 所在的值赋给变量 x。
- *e1 := e2:将表达式 e2 的值写入到地址 e1 所在的位置。
注意:堆和存储的更新在语法上是不同的。
2.2 Heap Read Rule (Simplified)

堆读取规则描述了从堆中读取数据的过程。简化版的堆读取规则为:
- 当变量x不在表达式e的地址集(ars(e))中时,我们可以读取存储位置e,得到值v,并将其赋值给x。也就是说,我们可以这样写:{e ↦ v} x := *e {x = v},表示将存储位置e的值v赋给变量x。
这个规则的应用例子:
- 如果s(y) = 19,执行命令x := *(y+1),并且如果y+1 ↦ 3 holds,那么执行后s(x) = 3。也就是说,将y+1的存储位置中的值3赋给了x。
如果变量 x 在表达式 e 的地址集中,我们需要更一般的规则,但这已超出了本次课程的讨论范围。
2.3 Assignment Rules

- HEAPW {e1 ↦ _} *e1 := e2 {e1 ↦ e2}:这是堆写入规则,表示将表达式 e2 的值写入到存储位置 e1 所在的位置。
- ASSIGN {x ≐ n} x := e {x ≐ e[n/x]}:这是基本赋值规则,表示将表达式 e 的值赋给变量 x。这里的 e[n/x] 表示将表达式 e 中的 x 替换为 n。
- ASSIGN’ (x /∉ vars(e)) / ({emp} x := e {x ≐ e}):这是特殊的赋值规则,只有当变量 x 不在表达式 e 中时,才可以使用。这表示将表达式 e 的值赋给变量 x。
2.4 Frame Rule

Frame 是一种用于跟踪命令 c 修改了哪些变量的工具。以下是一些基本的规则:
- modv(x := e) = {x}:表示命令 x := e 修改了变量 x。
- modv(x := *e) = {x}:表示命令 x := *e 修改了变量 x。
- modv(*e1 := e2) = {}:表示命令 *e1 := e2 没有修改任何变量。
- modv(while e do c) = modv(c):表示 while 循环修改了 c 修改的所有变量。
- modv(if e then ct else cf) = modv(ct) ∪ modv(cf):表示 if 语句修改了 ct 和 cf 修改的所有变量。
- modv(c1 ; c2) = modv(c1) ∪ modv(c2):表示命令序列 c1 ; c2 修改了 c1 和 c2 修改的所有变量。
Frame 规则 ({P} prog {Q} modv(prog) ∩ fv(R) = {}) / ({P ⋆ R} prog {Q ⋆ R}):表示如果 prog 修改的变量与 R 的自由变量 fv(R) 没有交集,则可以在 P 和 Q 上加一个 R 来得到新的断言。
2.5 Example Proof



这个程序的目的是交换两个指针x和y所指向的值。首先,我们初始化t和u为x和y的值,然后将u和t的值分别赋给x和y。根据Hoare逻辑,我们可以为这个过程创建三元组,并对每个步骤应用Hoare序列规则(Hoare sequencing rule)。Hoare序列规则是用于组合程序语句的一个规则,它允许我们将两个或多个程序语句串联在一起,并形成一个具有前提和后置条件的新的程序语句。
这个过程如下:
- {x ↦ vx ⋆ y ↦ vy} t := *x; {(x ↦ vx ∧ t = vx) ⋆ y ↦ vy}
- {(x ↦ vx ∧ t = vx) ⋆ y ↦ vy} u := *y; {(x ↦ vx ∧ t = vx) ⋆ (y ↦ vy ∧ u = vy)}
- {(x ↦ vx ∧ t = vx) ⋆ (y ↦ vy ∧ u = vy)} *x := u; {(x ↦ u ∧ t = vx) ⋆ (y ↦ vy ∧ u = vy)}
- {(x ↦ u ∧ t = vx) ⋆ (y ↦ vy ∧ u = vy)} *y := t; {x ↦ vy⋆ y ↦ vx}
在以上过程中,x ↦ vx表示指针x指向值vx,⋆表示堆中的分隔,即表示x和y指向的是堆中的不同位置。
2.6 Inductive Predicates 归纳谓词

归纳谓词是一种描述堆的工具,可以处理大小不定的堆。比如,e1 ↦ e2 和 emp 只能描述大小为 1 和 0 的堆,但我们如何描述更大的、或者说无界的堆数据结构呢?
例如,我们定义一个归纳谓词 list(e) 来表示一个链表。list(e) 的定义如下:(e = 0 ∧ emp) ∨ (∃e’. e ↦ e’ ⋆ list(e’))。也就是说,如果 e 是 0,那么表示一个空的链表;否则,e 指向一个元素 e’,并且 e’ 后面跟着一个链表。
2.7 Example: Tail
以下是一个使用了上述规则和概念的例子。这是一个简单的交换 x 和 y 的值的程序。
所以,我们成功地证明了这个程序可以交换 x 和 y 的值。
-
首先,我们假设 {x ↦ vx ⋆ y ↦ vy}。也就是说,变量 x 的值是 vx,变量 y 的值是 vy。
-
执行 t := *x。根据堆读取规则,我们可以将 x 的值 vx 赋给 t。所以,我们得到新的断言 {(x ↦ vx ∧ t = vx) ⋆ y ↦ vy}。
-
执行 u := *y。根据堆读取规则,我们可以将 y 的值 vy 赋给 u。所以,我们得到新的断言 {(x ↦ vx ∧ t = vx) ⋆ (y ↦ vy ∧ u = vy)}。
-
执行 *x := u。根据堆写入规则,我们可以将 u 的值 vy 写入 x 的位置。所以,我们得到新的断言 {(x ↦ u ∧ t = vx) ⋆ (y ↦ vy ∧ u = vy)}。
-
执行 *y := t。根据堆写入规则,我们可以将 t 的值 vx 写入 y 的位置。所以,我们得到新的断言 {x ↦ vy⋆ y ↦ vx}。
-
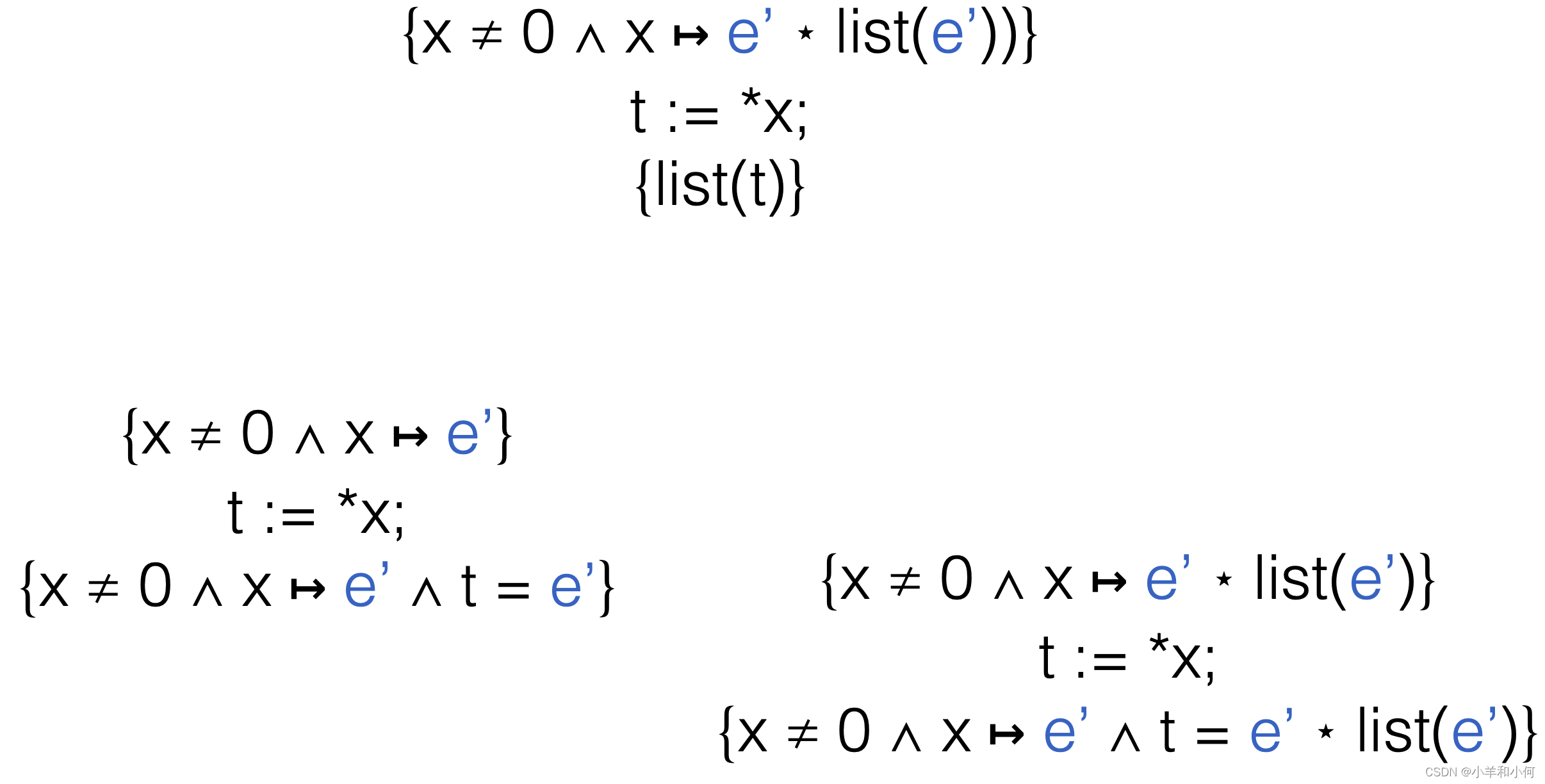
考虑另一个更复杂的例子,我们想要证明一个操作链表的程序。假设我们有一个链表,它的头是变量 x。
-
我们首先假设 {x ≠ 0 ∧ list(x)}。也就是说,x 不是 0,并且它指向一个链表。
-
执行 t := *x。根据堆读取规则,我们可以将 x 的值读入 t。所以,我们得到新的断言 {list(t)}。
-
为了证明这个断言,我们需要展开 list(t) 的定义。所以,我们得到新的断言 {x ≠ 0 ∧ (∃e’. x ↦ e’ ⋆ list(e’))}。
-
由于我们知道 x 的值被赋给了 t,所以我们得到新的断言 {x ≠ 0 ∧ x ↦ e’ ∧ t = e’}。同时,由于 x 指向一个链表,所以我们还有 {x ≠ 0 ∧ x ↦ e’ ∧ t = e’ ⋆ list(e’)}。
这就完成了证明。这个程序将链表的头赋值给了变量 t。
summary
堆是计算机内存中的一种动态数据结构,它通常被用来存储程序运行时产生的数据。然而,要表达堆中数据结构的行为可能非常复杂,因为我们需要考虑到所有可能的内存配置。为了解决这个问题,我们可以使用归纳谓词。
这里的slides中给出的一个归纳谓词的例子是list(e),它用来描述一个列表数据结构,它的定义如下:
list(e) = (e = 0 ∧ emp) ∨ (∃e’. e ↦ e’ ⋆ list(e’))
这个归纳谓词表示,一个列表要么是空的(即e = 0 ∧ emp,emp表示空堆),要么由一个元素和另一个列表组成(即存在一个元素e’使得e ↦ e’ ⋆ list(e’),这里的e ↦ e’表示e指向e’)。
在你提供的slides中,给出了使用这个归纳谓词的一个证明过程。这个过程就是从列表中取出第一个元素。我们首先定义前提条件{x ≠ 0 ∧ list(x)},然后执行t := *x;,最后得到后置条件{list(t)}。我们可以将归纳谓词展开来证明这个过程,如下:
- {x ≠ 0 ∧ (∃e’. x ↦ e’ ⋆ list(e’))} t := *x; {list(t)}
- {x ≠ 0 ∧ x ↦ e’ ⋆ list(e’)} t := *x; {list(t)}
- {x ≠ 0 ∧ x ↦ e’} t := *x; {x ≠ 0 ∧ x ↦ e’ ∧ t = e’}
- {x ≠ 0 ∧ x ↦ e’ ⋆ list(e’)} t := *x; {x ≠ 0 ∧ x ↦ e’ ∧ t = e’ ⋆ list(e’)}
这个过程中,我们在每一步都将归纳谓词进一步展开,直到我们可以清楚地看到在执行t := *x;之后,满足后置条件{list(t)}。