1 理论基础
标准粒子群算法通过追随个体极值和群体极值完成极值寻优,虽然操作简单,且能够快速收敛,但是随着迭代次数的不断增加,在种群收敛集中的同时,各粒子也越来越相似,可能在局部最优解周边无法跳出。混合粒子群算法摒弃了传统粒子群算法中的通过跟踪极值来更新粒子位置的方法,而是引入了遗传算法中的交叉和变异操作,通过粒子同个体极值和群体极值的交叉以及粒子自身变异的方式来搜索最优解。
2 案例背景
2.1 问题描述
旅行商问题(traveling saleman problem,TSP)又译为旅行推销员问题、货郎担问题,简称为TSP,是最基本的路线问题,该问题寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到起点的最小路径成本,最早的旅行商问题的数学模型是由Dantzig(1959)等人提出。旅行商问题是车辆路线问题(VRP)的特例,已证明旅行商问题是NP难题。
2.2 算法流程
基于混合粒子群算法的TSP算法流程如图15-1所示。

其中,种群初始化模块初始化粒子群种群;适应度值计算模块计算粒子群个体的适应度值;更新粒子模块根据粒子适应度值更新个体最优粒子和群体最优粒子;个体最优交叉把个体和个体最优粒子进行交叉得到新粒子;群体最优交叉把个体和群体最优粒子进行交叉得到新粒子;粒子变异是指粒子自身变异得到新粒子。
2.3 算法实现
1.个体编码
粒子个体编码采用整数编码的方式,每个粒子表示历经的所有城市,比如当历经的城市数为10,个体编码为[9 4 2 1 3 7 6 10 8 5],表示城市遍历从9开始,经过4,2,1,3,…最终返回城市9,从而完成TSP遍历。
2.适应度值
粒子适应度值表示为遍历路径的长度,计算公式为
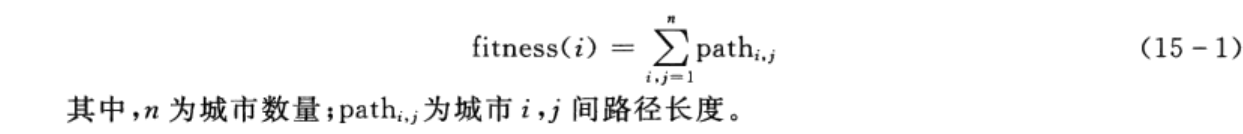
3.交叉操作
个体通过和个体极值和群体极值交叉来更新,交叉方法采用整数交叉法。首先选择两个交叉位置,然后把个体和个体极值或个体与群体极值进行交叉,假定随机选取的交叉位置为3和5,操作方法如下:

对得到的新个体采用了保留优秀个体策略,只有当新粒子适应度值好于旧粒子时才更新粒子。
4.变异操作
变异方法采用个体内部两位互换方法,首先随机选择变异位置pos1和pos2,然后把两个变异位置互换,假设选择的变异位置为2和4,变异操作如下所示:

对得到的新个体采用了保留优秀个体策略,只有当新粒子适应度值好于旧粒子时才更新粒子。
3 MATLAB程序实现
根据混合粒子群算法原理,在MATLAB中编程实现基于混合粒子群的TSP搜索算法。
3.1 适应度函数
适应度函数计算个体适应度值,个体适应度值为路径总长度,代码如下:
function indiFit=fitness(x,cityCoor,cityDist)
%% 该函数用于计算个体适应度值
%x input 个体
%cityCoor input 城市坐标
%cityDist input 城市距离
%indiFit output 个体适应度值
m=size(x,1);
n=size(cityCoor,1);
indiFit=zeros(m,1);
for i=1:m
for j=1:n-1
indiFit(i)=indiFit(i)+cityDist(x(i,j),x(i,j+1));
end
indiFit(i)=indiFit(i)+cityDist(x(i,1),x(i,n));
end3.2主函数
%% 该文件演示基于TSP-PSO算法
clc;clear
%% 下载数据
data=load('eil51.txt');
cityCoor=[data(:,2) data(:,3)];%城市坐标矩阵
figure
plot(cityCoor(:,1),cityCoor(:,2),'ms','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
legend('城市位置')
ylim([4 78])
title('城市分布图','fontsize',12)
xlabel('km','fontsize',12)
ylabel('km','fontsize',12)
%ylim([min(cityCoor(:,2))-1 max(cityCoor(:,2))+1])
grid on
%% 计算城市间距离
n=size(cityCoor,1); %城市数目
cityDist=zeros(n,n); %城市距离矩阵
for i=1:n
for j=1:n
if i~=j
cityDist(i,j)=((cityCoor(i,1)-cityCoor(j,1))^2+...
(cityCoor(i,2)-cityCoor(j,2))^2)^0.5;
end
cityDist(j,i)=cityDist(i,j);
end
end
nMax=200; %进化次数
indiNumber=1000; %个体数目
individual=zeros(indiNumber,n);
%^初始化粒子位置
for i=1:indiNumber
individual(i,:)=randperm(n);
end
%% 计算种群适应度
indiFit=fitness(individual,cityCoor,cityDist);
[value,index]=min(indiFit);
tourPbest=individual; %当前个体最优
tourGbest=individual(index,:) ; %当前全局最优
recordPbest=inf*ones(1,indiNumber); %个体最优记录
recordGbest=indiFit(index); %群体最优记录
xnew1=individual;
%% 循环寻找最优路径
L_best=zeros(1,nMax);
for N=1:nMax
N
%计算适应度值
indiFit=fitness(individual,cityCoor,cityDist);
%更新当前最优和历史最优
for i=1:indiNumber
if indiFit(i)<recordPbest(i)
recordPbest(i)=indiFit(i);
tourPbest(i,:)=individual(i,:);
end
if indiFit(i)<recordGbest
recordGbest=indiFit(i);
tourGbest=individual(i,:);
end
end
[value,index]=min(recordPbest);
recordGbest(N)=recordPbest(index);
%% 交叉操作
for i=1:indiNumber
% 与个体最优进行交叉
c1=unidrnd(n-1); %产生交叉位
c2=unidrnd(n-1); %产生交叉位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=tourPbest(i,chb1:chb2);
ncros=size(cros,2);
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
%插入交叉区域
xnew1(i,n-ncros+1:n)=cros;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
% 与全体最优进行交叉
c1=round(rand*(n-2))+1; %产生交叉位
c2=round(rand*(n-2))+1; %产生交叉位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=tourGbest(chb1:chb2);
ncros=size(cros,2);
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
%插入交叉区域
xnew1(i,n-ncros+1:n)=cros;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
%% 变异操作
c1=round(rand*(n-1))+1; %产生变异位
c2=round(rand*(n-1))+1; %产生变异位
while c1==c2
c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1;
end
temp=xnew1(i,c1);
xnew1(i,c1)=xnew1(i,c2);
xnew1(i,c2)=temp;
%新路径长度变短则接受
dist=0;
for j=1:n-1
dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
if indiFit(i)>dist
individual(i,:)=xnew1(i,:);
end
end
[value,index]=min(indiFit);
L_best(N)=indiFit(index);
tourGbest=individual(index,:);
end
%% 结果作图
figure
plot(L_best)
title('算法训练过程')
xlabel('迭代次数')
ylabel('适应度值')
grid on
figure
hold on
plot([cityCoor(tourGbest(1),1),cityCoor(tourGbest(n),1)],[cityCoor(tourGbest(1),2),...
cityCoor(tourGbest(n),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
hold on
for i=2:n
plot([cityCoor(tourGbest(i-1),1),cityCoor(tourGbest(i),1)],[cityCoor(tourGbest(i-1),2),...
cityCoor(tourGbest(i),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
hold on
end
legend('规划路径')
scatter(cityCoor(:,1),cityCoor(:,2));
title('规划路径','fontsize',10)
xlabel('km','fontsize',10)
ylabel('km','fontsize',10)
grid on
ylim([4 80])4仿真结果
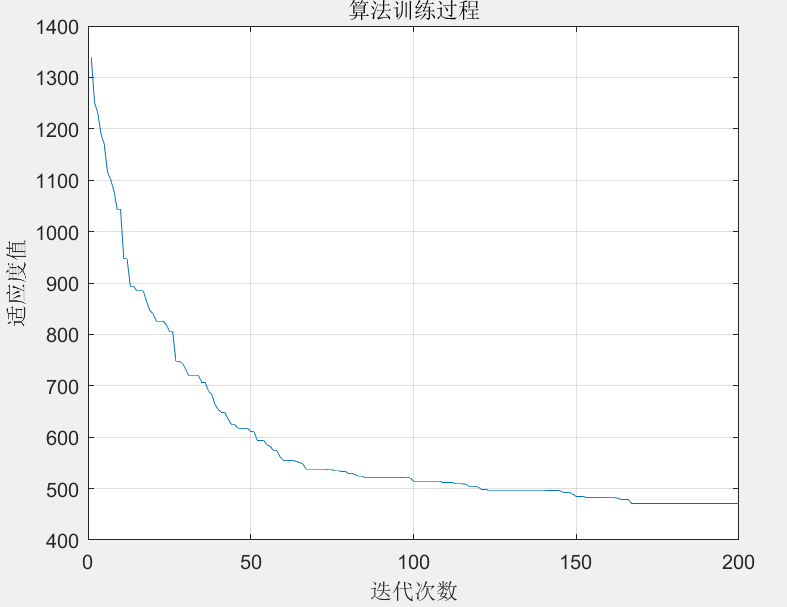
采用混合粒子群算法规划TSP路径,各城市的初始位置如图15-2所示。混合粒子群算法的进化次数为100,种群规模为100,算法进化过程中最优粒子适应度值变化和规划出的最优路径如图15-3和图15-4所示。
从图15-3与图15-4可以看到,混合粒子群算法能够较快找到连接各个城市的最优
路径。

 对于更大规模的TSP问题,同样可以采用粒子群算法进行求解,运行结果如下:
对于更大规模的TSP问题,同样可以采用粒子群算法进行求解,运行结果如下: