前言:
前面我们介绍了初阶二叉树的相关知识,二叉树常考的还是链式二叉树,而且二叉树也会考很多选择题,本文重点是在给出一些常考的二叉树的性质定理推导和经典练习题目配合强化巩固知识。
目录
一、二叉树的常见性质定理
二、常见性质定理的考察题目
三.金句频道
一、二叉树的常见性质定理
1. 若一个二叉树有n个节点,则该二叉树共有(n-1)条边。
证明:任意给出一棵二叉树,其中的每一个节点都有一个前驱节点(根节点除外),我们将一个节点和该节点指向它的前驱的点绑定看做一组,这样,对于二叉树的每一个节点,除根节点外,都有一个节点配成指向前驱的边,假设总共有n个节点,那么就有n-1条边(根节点没有指向前驱的边)。

2.若规定 根结点的层数为 1 ,则一棵 非空二叉树的第 i 层上最多有 2^(i-1) (i>0) 个结点。
我们知道,只有满二叉树的每一层的节点数是最多的,我们可以自己画出一棵满二叉树,比较容易的就可以发现这个规律,注意,这是建立在根节点是第一层的前提下的。
3.若规定只有根结点的二叉树的深度为1,则深度为 k 的二叉树最多有 2^k -1 个节点。
最多一定就是就是满二叉树了,这一点我们利用等比数列求和即可得出,等比数列求和公式为:

深度为k代表有k项,将k带入可得到:2^k -1
4.对于任何一棵二叉树,如果其叶节点数为 n0,度为 2 的节点总数为n2,则 n0=n2+1。
证明:假设一棵二叉树的度为0的节点有n0个,度为2的节点有n2个,度为1的节点有n1个,假设二叉树共有n个节点,所以有:
n0 + n1 + n2 = n
该二叉树包含的边总数为:n - 1
度为0的节点的边的条数:0
度为1的节点的边的条数:1
度为2的节点的边的条数:2
所以有:
n - 1 = n1 + 2*n2
n=n0 + n1 + n2 ; 也即 n0 = n2 + 1
5.具有 n 个结点的完全二叉树的深度 k为log(n+1)上取整 。
完全二叉树只允许最后一层缺少结点,所以说,如果我们按最大节点个数(即满二叉树)计算的话,那么我们可以利用性质三:
2^k -1 >= n
2^k>=n+1
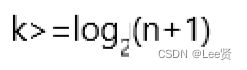
向上取整顾名思义,类似于3.1向上取整到4即可,因为我们是按满二叉树计算的,所以实际节点数肯定小于等于满二叉树时的节点,但是最后一层不满但是深度还是相当于满二叉树的深度,所以需要向上取整。
6.对于具有 n 个结点的完全二叉树 ,如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ,则对于 序号为 i 的结点有 :
若i>0 ,则其 父结点序号为: (i-1)/2 ;
若2i+1<n,则其左孩子序号为: 2i+1; 否则无左孩子。
若2i+2<n ,则其右孩子序号: 2i+2; 否则无右孩子。
当然,这里也是要分情况的,一般按这种下标的建树方式,称之为二叉树的顺序结构,但是这样也会存在问题,比如,如果一个节点没有左孩子,只有右孩子,我该不该把左孩子的节点空出来,以此来保持后续节点的逻辑关系不会因为确实而发生改变呢?比如下面的情况:
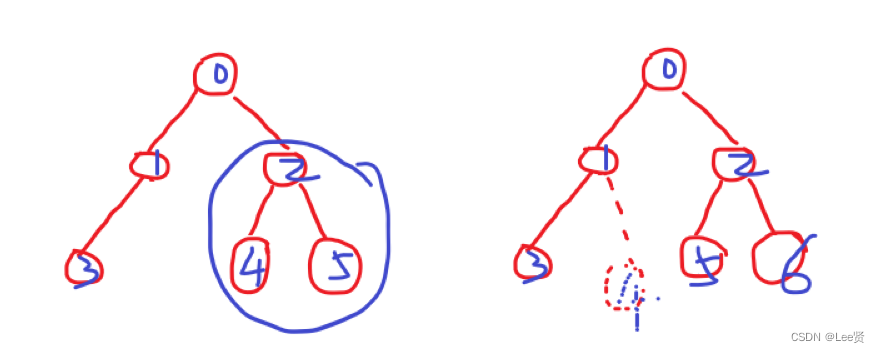
所以,一般情况下,我们的二叉树采用数组的方式的顺序实现只是用于满二叉树或者完全二叉树的情况,可以大大提高空间的利用率,该种实现方法也比较常见的用于堆排序等设计建大根堆小根堆 问题去,具体可以参考二叉树初阶和堆的详解。
二、常见性质定理的考察题目
这部分比较考验我们对二叉树的相关的基础概念,比如二叉树的度,结点之间的关系,不同类型的二叉树之间的关系,为了提高我们的思考能力,这里一律将选择题视作填空题展示,希望读者能够边读题边思考。
1.

二叉树的度:在二叉树中,每个节点最多只能有两个子节点,因此每个节点的度最大为2,即最多只有2个子节点。而节点的度指的是该节点拥有的子节点数,因此二叉树的度不同于一般意义上的度。在二叉树中,节点的度只能是0、1或2三种情况。
而树的度不受二叉树的限制,所以树能有无穷多个度,上不封顶,我们回到题目,一棵度为三的树,就代表这个树中每个结点最多只有三个孩子,我们假设这棵树的总的结点个数为n个,则n=n0+n1+n2+n3;其中叶子结点的度为0,也就是n0,其他的同理;我们还可以知道,一棵树的一个结点必然有一个前驱(根节点除外),所以一个由n个结点组成的树,它的边数就有n-1条,我们可以根据边数和节点的关系来列出关系式,即
n-1=0*n0(0度节点产生0条边)+1*n1+2*n2+3*n3;
可得 n0+n1+n2+n3-1=n1+2*n2+n3;
即可求得 n0=6,也即叶子结点的个数为6个。
2.
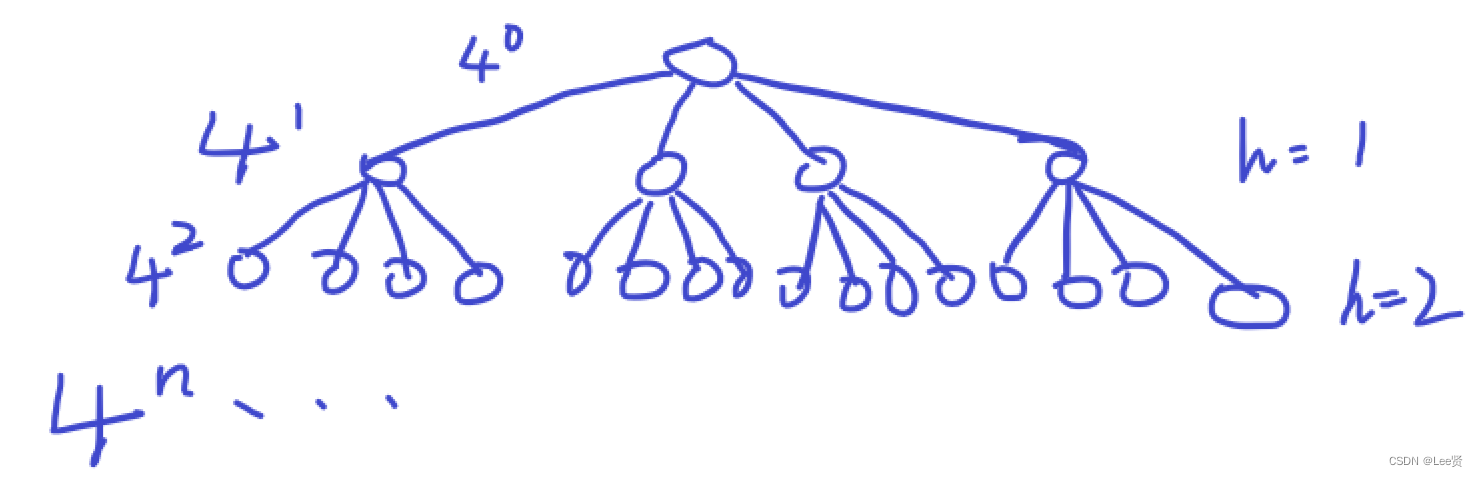
一棵树的度为4,代表这棵树的节点最多有四个子节点,而当这棵树每一层都是满的时,它的深度最小。也就是说,这棵树应当是一棵满四叉树。
假设高度为h,则由求二叉树节点个数的公式类比可知:根据等比数列求和公式得,这个数的节点个数为(4^h - 1) / 3。
当h = 5,最大节点数为341,当h = 6, 最大节点数为1365,所以,最小深度应该向上取整为6,此时的状态是前5层是满二叉树,第六层不是满二叉树。
3.
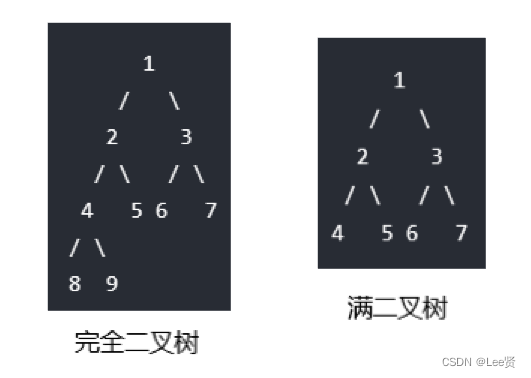
区分完全二叉树和满二叉树:
我们知道完全二叉树只有最后一层是不满的,所以完全二叉树直到倒数第二层都符合满二叉树的性质,我们知道k层满二叉树有2^k -1 个节点,而2^10-1=1023,2^9-1= 511,所以第九层一定是满的,到第十层出现了缺少节点的情况,1001-511=488,也就是剩余488个节点在最后一层,这489个节点没两个节点连到上面一层的一个节点上,我们可以容易的求出倒数第二层有2^8=256个节点,而最后一层剩余的488个节点需要每两个和这256个节点中的一个组成一棵子树,同时使倒数第二层的一个根节点变为度为2的节点,489/2=244,所以这样的节点共有244个,所以上层就会剩余256-244=12个叶子结点产生,最终的叶子结点个数为489+12=500个。
此外,我们还可以利用这样的一个结论:在完全二叉树中,如果节点总个数为奇数,则没有度为1的节点,如果节点总个数为偶数,只有一个度为1的节点。
因此:n0 + n1 + n2 = 1001 节点总数为奇数,没有度为1的节点
n0 + 0 + n2 = 2*n0-1 = 1001
n0 = 501
4.

由题意得(不知道写啥,写它就对了,嘿嘿),假设总的节点个数为n,度为2的节点为n2,由我们上面的性质4可以直接得出n2=3-1=2,那就直接n=n2+3+8=13,完事了,怎么样,简单吧。
5.

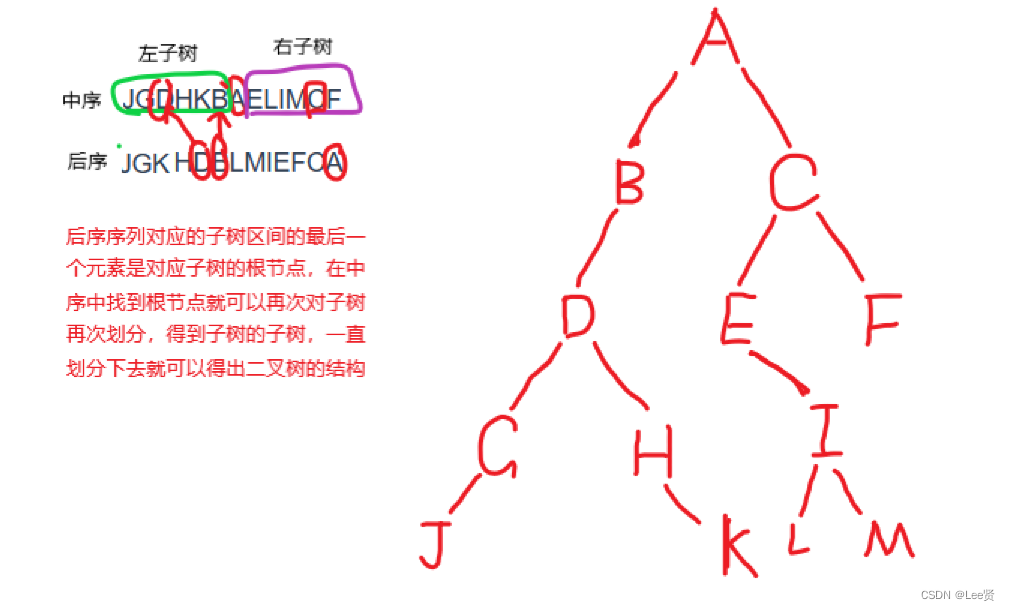
这种题目就是经典的由先(后)序遍历+中序遍历建二叉树的思想,具体详见二叉树的相关题目及其功能的实现中的二叉树创建的第一种方式。
这里我们就先解题为主:
这里具体过程需要递归实现,感兴趣的可以看上面的参考,里面有具体实现方式,这里只是讲一下原理,
6.

直接上性质吧,m个度为0的节点,那么根据性质4就可以得出度为2的节点有m-1个,根据题意,没有度为1的节点,那节点总数就直接是m+m-1=2*m-1了。
7.
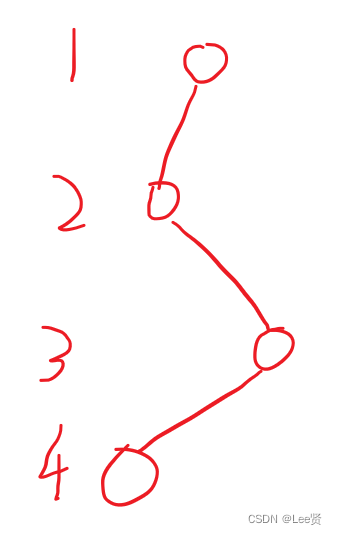
这个题,我们不能只考虑到满二叉树的情况,试想一下,一层有一个节点是不是深度就会更大呢?像这样:
所以说,我们的取值范围是[log(n+1),n];
8.
这个题,看起来不是那么好做,我们需要分很多种情况,并且容易漏掉一些情况,
首先这棵二叉树的高度一定在3~4层之间:
三层:(其中()表示该处为空()内部代表节点的子树部分)
A(B(C,D),()), A((),B(C,D)), A(B(C,()),D), A(B((),C),D),
A(B,C(D,())), A(B,C((),D))
四层:
如果为四层,就是单边树,每一层只有一个节点,除过根节点,其他节点都有两种选择,在上层节点的左边还是右边,所以2^3共8种
总共为14种。
9.
我们知道先序遍历序列是根-左-右,而后序遍历序列是左-右-根,那么该二叉树一定都没有左孩子或者都没有右孩子,并且它们都满足一个性质,就是节点数等于树高,也就是每一层只有一个节点。
三.金句频道
先沉淀,再厚积薄发
哈佛大学的校训之一:你所浪费的今天,是昨天死去的人所奢望的明天,你所厌恶的现在,是未来你回不到的曾经。
要么全力以赴,要么果断放弃。明确生活的态度会让一切变得简单,过多模棱两可,犹豫不决,只会在是非中迷失自我。要记住:种一棵树最好的时间是在十年前,其次是现在。每一个优秀的人都有一段沉默的时光,那段时光是付出很多努力却得不到结果的日子。我管它叫,扎根,沉淀,积累。
所以不要着急,不要老是觉得为什么我努力了还是没有效果。好好静下心来,认准一个方向,不断积累沉淀。“不积跬步,无以至千里;不积小流,无以成江河。”你只管努力沉淀积累,时间会给你惊喜。

小云彩,大梦想