传染病模型:原理介绍与应用实战
一、概述
在公共卫生研究中,传染病模型是一种关键的理论工具,用于理解和预测传染病的传播方式。
二、传染病模型原理
2.1 SIR模型
SIR模型是描述感染性传播病病人数量变化最简单的模型之一。其中,S代表易感者(Susceptible),即还未感染病毒但有可能感染的人群;I代表感染者(Infectious),即已经感染病毒并能够传播病毒的人群;R代表康复者(Recovered),即已经从病毒感染中康复并具有免疫力的人群。
在这个模型中,有两个重要的参数:感染率β和康复率γ。感染率描述了感染者每天接触并成功感染易感者的概率,康复率描述了感染者康复成免疫者的概率。
2.2 SEIR模型
SEIR模型是在SIR模型的基础上增加了暴露者(Exposed)的类别。E类的人群是已经被感染,但是还没有发病,也无法传播病毒。此外,SEIR模型中引入了潜伏期。
这两个模型的关键在于它们的动力学方程,通过微分方程来描述疾病的传播过程。
三、Python实战:COVID-19疫情模拟
利用Python进行SIR模型的模拟。我们的目标是对COVID-19疫情的传播进行模拟。
3.1 数据准备
首先,我们需要准备一些初始参数。这些参数基于COVID-19疫情的一些基本信息。
import numpy as np
import matplotlib.pyplot as plt
# 配置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为黑体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像时负号'-'显示为方块的问题
# 初始参数
N = 10000 # 总人口数
I0 = 1 # 初始感染者人数
R0 = 0 # 初始康复者人数
S0 = N - I0 - R0 # 初始易感者人数
beta = 0.3 # 感染率
gamma = 0.1 # 康复率
T = 160 # 模拟时间
3.2 模型构建
我们定义SIR模型的微分方程,然后使用scipy的odeint函数进行数值积分。
from scipy.integrate import odeint
# SIR模型的微分方程
def deriv(y, t, N, beta, gamma):
S, I, R = y
dSdt = -beta * S * I / N
dIdt = beta * S * I / N - gamma * I
dRdt = gamma * I
return dSdt, dIdt, dRdt
# 初始条件
y0 = S0, I0, R0
# 时间网格
t = np.linspace(0, T, T)
# 求解SIR模型
ret = odeint(deriv, y0, t, args=(N, beta, gamma))
S, I, R = ret.T
3.3 结果可视化
接下来,我们可以将模拟结果进行可视化。
import matplotlib.pyplot as plt
# 绘图
fig = plt.figure(facecolor='w')
ax = fig.add_subplot(111, axisbelow=True)
ax.plot(t, S/1000, 'b', alpha=0.5, lw=2, label='易感者')
ax.plot(t, I/1000, 'r', alpha=0.5, lw=2, label='感染者')
ax.plot(t, R/1000, 'g', alpha=0.5, lw=2, label='康复者')
ax.set_xlabel('时间(天)')
ax.set_ylabel('人数(千人)')
ax.grid(True, which='major', color='w', linewidth=2, linestyle='-') # 修改关键字参数
legend = ax.legend()
# 显示图形
plt.show()
结果如图:
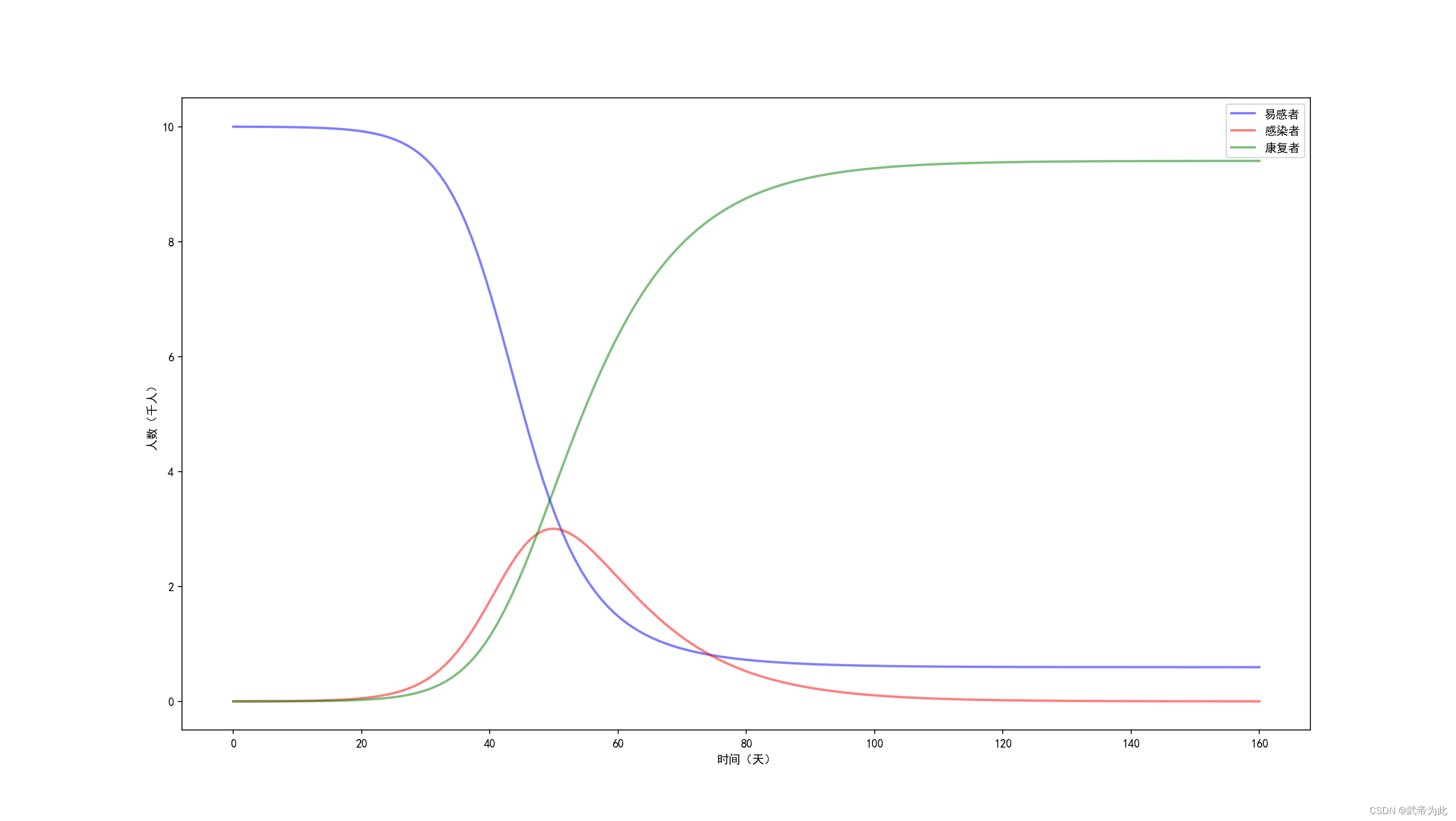
在这个模拟中,我们可以看到疾病的传播过程,以及感染者人数的峰值和康复者人数的增长。