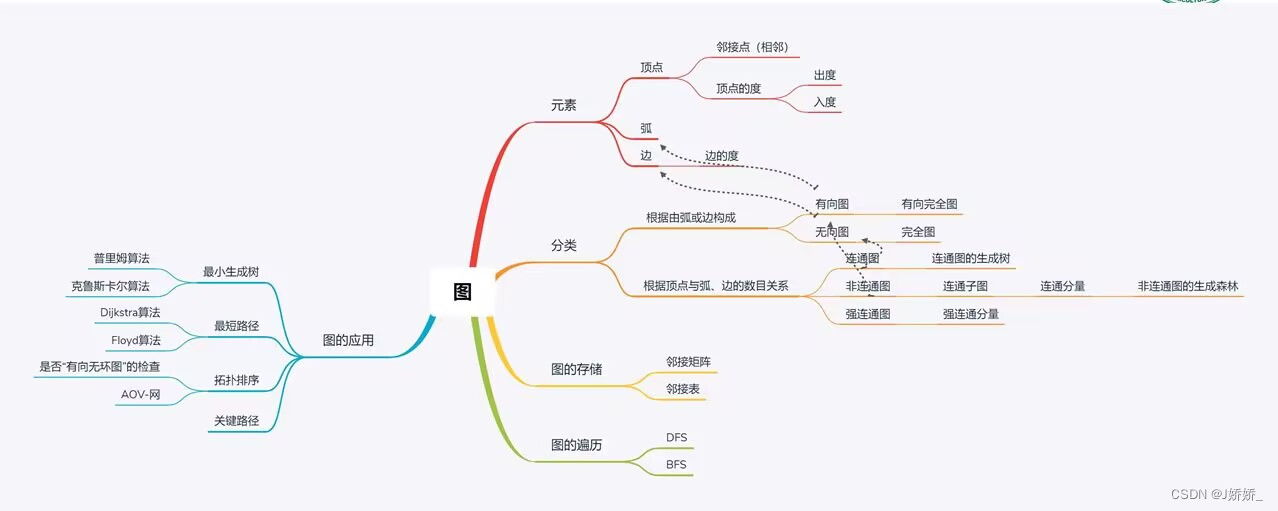
目录
1.图的基本术语
2.图的存储
2.1邻接矩阵
2.2.邻接表
3.图的遍历
3.1 深度搜索 dfs
3.2 广度搜索 bfs
4.图的应用
4.1 最小生成树
4.1.1 普里姆算法
4.1.2 克鲁斯卡尔算法
4.2 最短路径
4.2.1 Dijkstra算法
4.2.2 Floyd算法
4.3 拓扑排序
4.4 关键路径
一些练习
1.图的遍历及连通性
2.犯罪团伙
3.有向无环图的判定
2.Jungle Roads
3.迪杰斯特拉最短路径
弗洛伊德求最短路径
欧拉回路
有向无环图的拓扑排序
拓扑排序和关键路径
【数据结构】经典习题_数据结构题目_Huang_ZhenSheng的博客-CSDN博客
1.图的基本术语
2.图的存储
2.1 邻接矩阵
【数据结构】图的存储结构—邻接矩阵_图的邻接矩阵_路遥叶子的博客-CSDN博客
数据结构:邻接矩阵_Andy℡。的博客-CSDN博客
#define Maxlnt 32767 //表示极大值,即 ∞
#define MVNum 100 //最大顶点数
typedef char VerTexType; //设顶点的数据类型为字符型
typedef int ArcType; //假设边的权值类型为整型
typedef struct{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum,arcnum; //图的当前点数和边数
}AMGraph; //Adjacency Matrix Graph2.2 邻接表
图的存储结构——邻接表_图的邻接表_Charming Boy的博客-CSDN博客
【数据结构】图的存储结构—邻接表_图的邻接表存储_路遥叶子的博客-CSDN博客
//边的结点结构
#define MVNum 100 //最大顶点数
typedef struct ArcNode{
int adjvex; //该边所指向的顶点的位置
struct ArcNode *nextarc;//指向下一条边的指针
Otherinfo info; //和边相关的信息 有无都可
}ArcNode;
//顶点的结点结构
typedef struct VNode{
VerTexType data;//顶点信息、
ArcNode *firstarc;//指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum];//AdjList表示邻接表类型
//图的结构定义
typedef struct{
AdjList vertices; //定义一个数组vertices,是vertex的复数形式
int vexnum,arcnum; //图的当前顶点数和弧数
}ALGraph;3.图的遍历
图的遍历_爱编程的大李子的博客-CSDN博客
3.1 深度搜索 dfs
DFS入门级(模板)_dfs c语言_ღ江晚吟的博客-CSDN博客
DFS (深度优先搜索) 算法详解 + 模板 + 例题,这一篇就够了_深度优先搜索经典例题_21岁被迫秃头的博客-CSDN博客
3.2 广度搜索 bfs
C++算法——BFS(图解)_bfs c++_隰有游龙的博客-CSDN博客
BFS(广度优先算法)_bfs算法为什么要q.pop_1234_6的博客-CSDN博客
4.图的应用
4.1 最小生成树
最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示_哔哩哔哩_bilibili
4.1.1 普里姆算法
#include<iostream>
#include<malloc.h>
using namespace std;
#define MaxVertexNum 100
#define INFINITY 30000
typedef struct{
int adjVertex; //某定点与已构造好的部分生成树的顶点之间权值最小的顶点
int lowCost; //某定点与已构造好的部分生成树的顶点之间的最小权值。
}CloseEdge; //辅助数组
typedef int EdgeType; //边的数据类型
typedef struct{
int Vex[MaxVertexNum]; //定点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表,
//存放边的权值,如果为Edge[i][j]=INFINITY,则表示顶点i,j之间无边
int vernum,arcnum; //图的当前顶点数和弧数
}MGraph; //适合存储稠密图
//邻接矩阵法创建一个图
void CreateMGraph(MGraph *G)
{
int i,j,k,w;
printf("请输入图的顶点数和边数:");
cin>>G->vernum>>G->arcnum;
printf("请输入图的各个顶点的信息(A,B…):");
for(i=0;i<G->vernum;i++)
cin>>G->Vex[i];//"%c"中%c后面要有空格
for(i=0;i<G->vernum;i++)
{
for(j=0;j<G->vernum;j++)
G->Edge[i][j]=INFINITY;
}
printf("请输入各条边的信息(例:1 2表示在A顶点和B顶点之间有一条边):\n");
for(k=0;k<G->arcnum;k++)
{//此为创建有向图的邻接矩阵
int Iindex,Jindex,weight;
cin>>Iindex>>Jindex>>weight;
G->Edge[Iindex][Jindex]=weight;
//如果加上G->Edge[j][i]=1;则建立的是无向图的邻接矩阵
G->Edge[Jindex][Iindex]=weight;
}
}
//输出图的邻接矩阵
void DisplayMGraph(MGraph G)
{
int i,j;
printf(" ");
for(i=0;i<G.vernum;i++)
printf("%d ",G.Vex[i]);
for(i=0;i<G.vernum;i++)
{
printf("\n%d\t",G.Vex[i]);
for(j=0;j<G.vernum;j++)
printf("%d ",G.Edge[i][j]);
}
}
//Prim算法求最小生成树
void MinSpanTree_PRIM(MGraph G,int u,CloseEdge closeEdge[])
{//从第u个顶点出发构造图G的最小生成树,最小生成树顶点信息存放在
//数组closeEdge中
int i,j,w,minindex,LowCost=0;
for(i=0;i<G.vernum;i++)
if(!u)
{
closeEdge[i].adjVertex=u;
closeEdge[i].lowCost=G.Edge[u][i];
}
closeEdge[u].lowCost=0; /*初始,U={u}*/
for(i=0;i<G.vernum-1;i++)/*选择加入其余G.vernum-1个结点*/
{
w=INFINITY;
for(j=0;j<G.vernum;j++)/*在辅助数组closeEdge中选取权值最小的顶点*/
{
if(closeEdge[j].lowCost!=0&&closeEdge[j].lowCost<w)
{
w=closeEdge[j].lowCost;
minindex=j;
}
}
LowCost+=w;//将最小边权值加入最小代价
closeEdge[minindex].lowCost=0; /*将第minindex顶点并入U集*/
for(j=0;j<G.vernum;j++)/*新顶点并入U后,修改辅助数组*/
{
if(G.Edge[minindex][j]<closeEdge[j].lowCost)
{
closeEdge[j].adjVertex=minindex;
closeEdge[j].lowCost=G.Edge[minindex][j];
}
}
}
printf("生成树的各边为:\n");
for(i=0;i<G.vernum;i++)/*打印最小生成树的各条边*/
{
if(i!=u)
printf("\n%d->%d,%d",i,closeEdge[i].adjVertex,G.Edge[i][closeEdge[i].adjVertex]);
}
printf("\n构造生成树的总代价为:%d\n",LowCost);
}
int main()
{
MGraph G;
CloseEdge closeEdge[MaxVertexNum];
CreateMGraph(&G);
DisplayMGraph(G);
MinSpanTree_PRIM(G,0,closeEdge);
return 0;
}
4.1.2 克鲁斯卡尔算法
核心算法
void Kruskal(AMGraph &G){
Edge edge;
InitailEdge(G,edge);
sort(G,edge);
// ShowEdge(G,edge);
for(int i=0;i<G.vexnum;i++){
Vexset[i] = i;//每个节点自成一个分量
}
int headi,taili;//边起点的下标、边终点的下标
int headt,tailt;//操作连通分量时的中间量
for(int i=0;i<G.arcnum;i++){
headi = LocateVex(G,edge[i].Head);
taili = LocateVex(G,edge[i].Tail);
headt = Vexset[headi];
tailt = Vexset[taili];
if(headt!=tailt){//如果两个点不是同一个连通分量
cout<<edge[i].Head<<"-"<<edge[i].lowcast<<"-"<<edge[i].Tail<<endl;
for(int j=0;j<G.vexnum;j++){
if(Vexset[j]==headt){//合并选出来的两个节点,使其处于同一个连通分量
Vexset[j] = tailt;
}
}
}
}
}
代码
#include<iostream>
#include<stdio.h>
using namespace std;
typedef char VerTexType;
typedef int ArcType;
#define MaxInt 32767
#define MVNum 100
#define ArcNum 100
#define OK 1
#define ERROR -1
int Vexset[MVNum];//辅助数组表示连通分量
typedef int status;
typedef struct{
VerTexType vexs[MVNum] {'A','B','C','D','E','F'};
ArcType arcs[MVNum][MVNum];
int vexnum = 6,arcnum = 10;
}AMGraph;
typedef struct{
VerTexType Head;//起点
VerTexType Tail;//终点
ArcType lowcast;
}Edge[ArcNum];
status CreateUDN(AMGraph &G){//创建无向图
for(int i=0;i<G.vexnum;i++){
for(int j=0;j<G.vexnum;j++){
if(i==j){
G.arcs[i][j] = 0;
}else
G.arcs[i][j] = MaxInt;//初始状态全部节点之间相互不可达
}
}
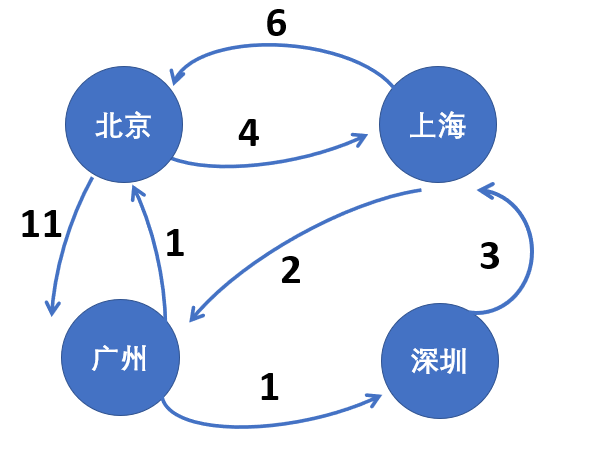
G.arcs[0][1]=6;G.arcs[0][2]=1;G.arcs[0][3]=5;
G.arcs[1][2]=5;G.arcs[1][4]=3;
G.arcs[2][3]=5;G.arcs[2][4]=6;G.arcs[2][5]=4;
G.arcs[3][5]=2;
G.arcs[4][5]=6;
for(int i=0;i<G.vexnum;i++){
for(int j=i+1;j<G.vexnum;j++){
if(G.arcs[i][j]!=MaxInt){
G.arcs[j][i] = G.arcs[i][j];
}
}
}//矩阵对称
return OK;
}
void ShowGraph(AMGraph G){
cout<<" ";
for(int i=0;i<G.vexnum;i++){
cout<<" "<<G.vexs[i];
}
cout<<endl;
for(int i=0;i<G.vexnum;i++){
cout<<G.vexs[i]<<" ";
for(int j=0;j<G.vexnum;j++){
if(G.arcs[i][j]==MaxInt){
cout<<"* ";
}else{
cout<<G.arcs[i][j]<<" ";
}
}
cout<<endl;
}
}
int LocateVex(AMGraph G, VerTexType v){
int i;
for(i=0;i<G.vexnum;i++){
if(G.vexs[i]==v){
return i;
}
}
return ERROR;
}
VerTexType Transform(AMGraph G, int vn){
return G.vexs[vn];
}
void InitailEdge(AMGraph G,Edge &edge){//初始化边表
int arcnum = 0;
for(int i=0;i<G.vexnum;i++){//纵列为起点
for(int j=i+1;j<G.vexnum;j++){//横行为终点
if(G.arcs[i][j]!=MaxInt&&G.arcs[i][j]!=0){
edge[arcnum].Head = Transform(G,i);
edge[arcnum].Tail = Transform(G,j);
edge[arcnum].lowcast = G.arcs[i][j];
arcnum++;
}
}
}
}
void sort(AMGraph G,Edge &edge){
VerTexType tv;
ArcType tl;
for(int i=0;i<G.arcnum;i++){
for(int j=0;j<G.arcnum-i-1;j++){
if(edge[j].lowcast>edge[j+1].lowcast){//直接写对象互换报错,忘记咋互换对象了,这样写有点麻烦,先将就着用吧 ,这个操作不是重点
tv = edge[j].Head;
edge[j].Head = edge[j+1].Head;
edge[j+1].Head = tv;
tv = edge[j].Tail;
edge[j].Tail = edge[j+1].Tail;
edge[j+1].Tail = tv;
tl = edge[j].lowcast;
edge[j].lowcast = edge[j+1].lowcast;
edge[j+1].lowcast = tl;
}
}
}
}
void ShowEdge(AMGraph G,Edge edge){
for(int i=0;i<G.arcnum;i++){
cout<<edge[i].Head<<"-"<<edge[i].lowcast<<"-"<<edge[i].Tail<<endl;
}
}
void ShowVexset(AMGraph G){
for(int i=0;i<G.vexnum;i++){
cout<<Vexset[i]<<" ";
}
cout<<endl;
}
void Kruskal(AMGraph &G){
Edge edge;
InitailEdge(G,edge);
// ShowEdge(G,edge);
sort(G,edge);
// ShowEdge(G,edge);
for(int i=0;i<G.vexnum;i++){
Vexset[i] = i;//每个节点自成一个分量
}
int headi,taili;//边起点的下标、边终点的下标
int headt,tailt;//操作连通分量时的中间量
for(int i=0;i<G.arcnum;i++){
headi = LocateVex(G,edge[i].Head); //起点下标
taili = LocateVex(G,edge[i].Tail); //终点下标
headt = Vexset[headi];//获取起点的连通分量
tailt = Vexset[taili];//获取终点的连通分量
if(headt!=tailt){//如果两个点不是同一个连通分量
cout<<edge[i].Head<<"-"<<edge[i].lowcast<<"-"<<edge[i].Tail<<endl;
for(int j=0;j<G.vexnum;j++){
if(Vexset[j]==headt){//更新Vexset数组,把改起点的连通分量改成和终点连通分量一致(其实就是合并连通分量)
Vexset[j] = tailt;
// ShowVexset(G);
}
}
}
}
}
int main(){
AMGraph G;
CreateUDN(G);
ShowGraph(G);
Kruskal(G);
return 0;
}
4.2 最短路径
4.2.1 Dijkstra算法
核心算法
void dijkstra(){
//源点为源点start。
int minn;//记录每趟最短路径中最小的路径值。
int pos;//记录得到的minn所对应的下标。
init();//调用初始化函数。
visited[start]=true;
for(int i=1;i<=n;i++){
//将n个顶点依次加入判断。
minn=inf;
for(int j=1;j<=n;j++){
if(!visited[j]&&dis[j]<minn){
minn=dis[j];
pos=j;
}
}
//经过这趟for循环后我们找到的就是我们想要的点,可以确定这点到源点的最终最短距离了。
visited[pos]=true;//我们将此点并入已知集合。
//接下来就是更新dis数组了,也就是当前最短距离,这都是针对还没有并入已知集合的点。
for(int j=1;j<=n;j++){
if(!visited[j]&&dis[j]>dis[pos]+graph[pos][j])
dis[j]=dis[pos]+graph[pos][j];
}
}
//退出循环后,所有的点都已并入已知集合中,得到的dis数组也就是最终最短距离了。
cout<<dis[goal]<<endl;//输出目标点到源点的最短路径长度。
}
4.2.2 Floyd算法
Floyd - Warshall(弗洛伊德算法)_floyd-warshall_D小冰的博客-CSDN博客
七、最短路径——弗洛伊德(Floyd)算法_floyd算法求最短路径问题_瘦弱的皮卡丘的博客-CSDN博客
4.3 拓扑排序
-是否“有向无环图”的检查
-AOV网
数据结构C++——拓扑排序_拓扑排序c++_近景_的博客-CSDN博客
#include<iostream>
#include<string>
using namespace std;
#define MVNum 100
#define OK 1
#define ERROR 0
#define MaxInt 100
typedef string VerTexType;
typedef int Status;
typedef int SElemType;
//栈
typedef struct{
SElemType* base;
SElemType* top;
int stacksize;
}SqStack;
//边结点
typedef struct ArcNode {
int adjvex;
struct ArcNode* nextarc;
}ArcNode;
//顶点结点
typedef struct VNode {
VerTexType data;
ArcNode* firstarc;
}VNode,AdjList[MVNum];
//图
typedef struct {
int vexnum, arcnum;
AdjList vertices;
}ALGraph;
/*--------拓扑排序辅助数组的存储结构--------*/
int indegree[MVNum];//存放各顶点入度
int topo[MVNum];//记录拓扑序列的顶点编号
Status InitStack(SqStack& S) {
S.base = new SElemType[MaxInt];
if (!S.base) return ERROR;
S.top = S.base;
S.stacksize = MaxInt;
return OK;
}
Status StackEmpty(SqStack S) {
if (S.top == S.base) return OK;
return ERROR;
}
Status Push(SqStack& S, SElemType e) {
if (S.top - S.base == S.stacksize) return ERROR;
*S.top = e;
S.top++;
return OK;
}
Status Pop(SqStack& S, SElemType& e) {
if (S.base == S.top) return ERROR;
S.top--;
e = *S.top;
return OK;
}
//顶点定位 v1 v2字符串转化为int数字
int LocateVex(ALGraph G, VerTexType v) {
for (int i = 0; i < G.vexnum; i++) {
if (G.vertices[i].data == v)
return i;
}
return -1;
}
//创建无向图
void CreateUDG(ALGraph& G) {
cin >> G.vexnum >> G.arcnum;
for (int i = 0; i < G.vexnum; i++)
{
cin >> G.vertices[i].data;
G.vertices[i].firstarc = NULL;//初始化表头结点的指针域为NULL
}
for (int k = 0; k < G.arcnum; k++)
{
VerTexType v1, v2;
cin >> v1 >> v2;
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);
ArcNode* p1 = new ArcNode;
p1->adjvex = j;
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p1;
}
}
//遍历一遍 确定每个顶点的入度
void FindInDegree(ALGraph G, int indegree[])
{
for (int i = 0; i < G.vexnum; i++) {
int cnt = 0;//设置变量存储邻接点域为i的结点个数
for (int j = 0; j < G.vexnum; j++) {
ArcNode* p = new ArcNode;//定义指向各个边结点的指针
p = G.vertices[j].firstarc;
while (p) {//当p未指到单个链表的末尾时继续循环
if (p->adjvex == i)//当某边结点邻接点域等于i时,计数变量++
cnt++;
p = p->nextarc;//指针不断向后指
}
indegree[i] = cnt;//将计数结果保留在indegree数组中
}
}
}
//拓扑排序
Status TopologicalSort(ALGraph G, int topo[]) {
//有向图G采用邻接表存储结构
//若G无回路,则生成G的一个拓扑排序topo[]并返回OK,否则ERROR
FindInDegree(G, indegree);//求出各结点的入度存入数组indegree中
SqStack S;
InitStack(S);//初始化栈
for (int i = 0; i < G.vexnum; i++) {
if (!indegree[i]) Push(S, i);//入度为0者进栈
}
int m = 0;//对输出顶点计数u,初始为0
while (!StackEmpty(S)) {
int i = 0;
Pop(S, i);//将栈顶顶点vi出栈
topo[m] = i;//将vi保存在拓扑序列数组topo中
++m;//对输出顶点计数
ArcNode* p = new ArcNode;
p = G.vertices[i].firstarc;//p指向vi的第一个邻接点
while (p != NULL) {
int k = p->adjvex;//vk为vi的邻接点
--indegree[k];//vi的每个邻接点的入度减一
if (indegree[k] == 0) Push(S, k);//若入度减为0,则入栈
p = p->nextarc;//p指向顶点vi下一个邻接结点
}
}
if (m < G.vexnum) return ERROR;//该有向图有回路
else return OK;
}
/*输出拓扑排序后的结果*/
void PrintResult(ALGraph G) {
if (TopologicalSort(G, topo)) {
for (int i = 0; i < G.vexnum; i++) {
cout << G.vertices[topo[i]].data << " ";
}
}
}
int main() {
ALGraph G;
CreateUDG(G);
PrintResult(G);
return 0;
}
4.4 关键路径*
图解:什么是关键路径?_ChatAlgorithm的博客-CSDN博客
【算法专题】关键路径及代码实现_关键路径代码实现_你好世界wxx的博客-CSDN博客
#include<bits/stdc++.h>
using namespace std;
// 边表结点声明
typedef struct EdgeNode
{
int adjvex;
struct EdgeNode *next;
}EdgeNode;
// 顶点表结点声明
typedef struct VertexNode
{
int in; // 顶点入度
int data;
EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes, numEdges;
}graphAdjList, *GraphAdjList;
int *etv, *ltv;
int *stack2; // 用于存储拓扑序列的栈
int top2; // 用于stack2的栈顶指针
// 拓扑排序算法
// 若GL无回路,则输出拓扑排序序列并返回OK,否则返回ERROR
Status TopologicalSort(GraphAdjList GL)
{
EdgeNode *e;
int i, k, gettop;
int top = 0; // 用于栈指针下标索引
int count = 0; // 用于统计输出顶点的个数
int *stack; // 用于存储入度为0的顶点
stack = (int *)malloc(GL->numVertexes * sizeof(int));
for( i=0; i < GL->numVertexes; i++ )
{
if( 0 == GL->adjList[i].in )
{
stack[++top] = i; // 将度为0的顶点下标入栈
}
}
// 初始化etv都为0
top2 = 0;
etv = (int *)malloc(GL->numVertexes*sizeof(int));
for( i=0; i < GL->numVertexes; i++ )
{
etv[i] = 0;
}
stack2 = (int *)malloc(GL->numVertexes*sizeof(int));
while( 0 != top )
{
gettop = stack[top--]; // 出栈
// printf("%d -> ", GL->adjList[gettop].data);
stack2[++top2] = gettop; // 保存拓扑序列顺序 C1 C2 C3 C4 .... C9
count++;
for( e=GL->adjList[gettop].firstedge; e; e=e->next )
{
k = e->adjvex;
// 注意要点!
// 将k号顶点邻接点的入度-1,因为他的前驱:下边这个if条件是分析整个程序的已经消除
// 接着判断-1后入度是否为0,如果为0则也入栈
if( !(--GL->adjList[k].in) )
{
stack[++top] = k;
}
if( (etv[gettop]+e->weight) > etv[k] )
{
etv[k] = etv[gettop] + e->weight;
}
}
}
if( count < GL->numVertexes ) // 如果count小于顶点数,说明存在环
{
return ERROR;
}
else
{
return OK;
}
}
// 求关键路径,GL为有向图,输出GL的各项关键活动
void CriticalPath(GraphAdjList GL)
{
EdgeNode *e;
int i, gettop, k, j;
int ete, lte;
// 调用改进后的拓扑排序,求出etv和stack2的值
TopologicalSort(GL);
// 初始化ltv都为汇点的时间
ltv = (int *)malloc(GL->numVertexes*sizeof(int));
for( i=0; i < GL->numVertexes; i++ )
{
ltv[i] = etv[GL->numVertexes-1];
}
// 从汇点倒过来逐个计算ltv
while( 0 != top2 )
{
gettop = stack2[top2--]; // 注意,第一个出栈是汇点
for( e=GL->adjList[gettop].firstedge; e; e=e->next )
{
k = e->adjvex;
if( (ltv[k] - e->weight) < ltv[gettop] )
{
ltv[gettop] = ltv[k] - e->weight;
}
}
}
// 通过etv和ltv求ete和lte
for( j=0; j < GL->numVertexes; j++ )
{
for( e=GL->adjList[j].firstedge; e; e=e->next )
{
k = e->adjvex;
ete = etv[j];
lte = ltv[k] - e->weight;
if( ete == lte )
{
printf("<v%d,v%d> length: %d , ", GL->adjList[j].data, GL->adjList[k].data, e->weight );
}
}
}
}一些练习
1.图的遍历及连通性
【问题描述】
根据输入的图的邻接矩阵A,判断此图的连通分量的个数。请使用邻接矩阵的存储结构创建图的存储,并采用BFS优先遍历算法实现,否则不得分。
【输入形式】
第一行为图的结点个数n,之后的n行为邻接矩阵的内容,每行n个数表示。其中A[i][j]=1表示两个结点邻接,而A[i][j]=0表示两个结点无邻接关系。
【输出形式】
输出此图连通分量的个数。
【样例输入】
5
0 1 1 0 0
1 0 1 0 0
1 1 0 0 0
0 0 0 0 1
0 0 0 1 0
【样例输出】
2
【样例说明】
邻接矩阵中对角线上的元素都用0表示。(单个独立结点,即与其它结点都没有边连接,也算一个连通分量)
#include<bits/stdc++.h>#include<bits/stdc++.h>
using namespace std;
int cmap[51][51]={0};
int n;
int visit[51];
int num=0;
void bfs()
{
int i=0;
queue<int> q;
for(i=0;i<n;i++)
{
if(!visit[i])
{
visit[i]=1;
num++;
q.push(i);
while(!q.empty())
{
i=q.front();
q.pop();
for(int j=0;j<n;j++)
{
if(cmap[i][j]==1&&visit[j]==0)
{
visit[j]=1;
q.push(j);
}
}
}
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
visit[i]=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>cmap[i][j];
bfs();
cout<<num;
}
2.犯罪团伙
| 【题目描述】 此题必须采用邻接表的存储结构,建立图的存储,然后采用DFS遍历实现求解。否则不给分。 警察抓到了 n 个罪犯,警察根据经验知道他们属于不同的犯罪团伙,却不能判断有多少个团伙,但通过警察的审讯,知道其中的一些罪犯之间相互认识,已知同一犯罪团伙的成员之间直接或间接认识。有可能一个犯罪团伙只有一个人。请你根据已知罪犯之间的关系,确定犯罪团伙的数量。已知罪犯的编号从 1 至 n。 【输入】 第一行:n(<=1000,罪犯数量),第二行:m(<5000,关系数量)以下若干行:每行两个数:I 和 j,中间一个空格隔开,表示罪犯 i 和罪犯 j 相互认识。 【输出】 一个整数,犯罪团伙的数量。 【样例输入】 11 8 1 2 4 3 5 4 1 3 5 6 7 10 5 10 8 9 【输出】 3 | 10.00 | 共有测试数据:1 平均占用内存:1.332K 平均CPU时间:0.00885S 平均墙钟时间:0.0088 |
#include <bits/stdc++.h>
using namespace std;
int i, j, c;
int visited[2000];
struct edgenode
{
int adjvex;
edgenode *next;
};
typedef struct vertexnode
{
edgenode *firstedge;
} adjlist[2000];
typedef struct
{
adjlist adj;
int numV, numE;
} graph;
void create(graph *g)
{
cin >> g->numV >> g->numE;
for (i = 0; i < g->numV; i++)
g->adj[i].firstedge = NULL;
for (int k = 0; k < g->numE; k++)
{
cin >> i >> j;
edgenode *e = new edgenode;
e->adjvex = j;
e->next = g->adj[i].firstedge;
g->adj[i].firstedge = e;
edgenode *q = new edgenode;
q->adjvex = i;
q->next = g->adj[j].firstedge;
g->adj[j].firstedge = q;
}
}
void dfs(graph *g, int i)
{
edgenode *p;
visited[i] = 1;
p = g->adj[i].firstedge;
while (p)
{
if (!visited[p->adjvex])
dfs(g, p->adjvex);
p = p->next;
}
}
void tra(graph *g)
{
int v;
c = 0;
for (v = 1; v <= g->numV; v++)
visited[v] = 0;
for (v = 1; v <= g->numV; v++)
if (!visited[v])
{
c++;
dfs(g, v);
}
}
int main()
{
graph g;
create(&g);
tra(&g);
cout << c;
}
3.有向无环图的判定
【题目描述】给定无权有向图G(V,E),请判断G是否是一个有向无环图(DAG)。
【输入格式】
第一行包含两个整数N、M,表示该图共有N个结点和M条有向边。(N <= 5000,M <= 200000)
接下来M行,每行包含2个整数{u,v},表示有一条有向边(u,v)
【输出格式】
有环输出“not DAG”,无环输出“DAG”
【输入样例】
5 7
1 2
1 5
2 3
3 1
3 2
4 1
4 5
【输出样例】
not DAG
not DAG
【注意】本题请使用两种不同的方法实现。结果输出两次。
//1.有向无环图的判定
#include<bits/stdc++.h>
using namespace std;
const int N = 100;
int n,a[100][100],edge;
int path[N], visited[N], cycle;
int DFS(int u, int start)
{
int i;
visited[u] = -1;
path[u] = start;
for (i = 0; i < n;i++)
{
if (a[u][i]&&i!=start)
{
if (visited[i]<0)
{
cycle = u;
return 0;
}
if (!DFS(i,u))
{
return 0;
}
}
}
visited[u] = 1;
return 1;
}
int main()
{
cin>>n>>edge;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=0;
int indegree[100];
for(int i=0;i<=n;i++)
indegree[i]=0;
while(edge--)
{
int v1,v2;
cin>>v1>>v2; //1 2
a[v1][v2]=1;
indegree[v2]++; //入度++
}
//用数组模拟一个栈
int stack[100],top=-1;
for(int i=1;i<=n;i++)
if(indegree[i]==0) stack[++top]=i;
while(top!=-1)
{
int i=stack[top];
top--;
for(int j=1;j<=n;j++) //到邻接矩阵的第i行去找每一列
{
if(a[i][j]==1)
{
indegree[j]--;
if(indegree[j]==0) stack[++top]=j;
}
}
}
cycle = -1;
for (int i = 0; i < n;i++)
{
if (!visited[i]&&!DFS(i,-1))
{
break;
}
}
if (cycle<0)
{
cout << "DAG" << endl;
}
else
{
cout << "not DAG" << endl;
}
int i;
for(i=1;i<=n;i++)
{
if(indegree[i]>0)
{
cout<<"not DAG";
return 0;
}}
cout<<"DAG";
return 0;
}
4.图形窗口问题
| 【问题描述】 在某图形操作系统中,有N个窗口,每个窗口都是一个两边与坐标轴分别平行的矩形区域。窗口的边界上的点也属于该窗口。窗口之间有层次的区别,在多于一个窗口重叠的区域里,只会显示位于顶层的窗口里的内容。 当你点击屏幕上一个点的时候,你就选择了处于被点击位置的最顶层窗口,并且这个窗口就会被移到所有窗口的最顶层,而剩余的窗口的层次顺序不变。如果你点击的位置不属于任何窗口,则系统会忽略你这次点击。 现在我们希望你写一个程序模拟点击窗口的过程。 【输入形式】 输入的第一行有两个正整数,即N和M。(1<=N<=10,1<=M<=10)接下来N行按照从最下层到最顶层的顺序给出N个窗口的位置。每行包含四个非负整数x1,y1,x2,y2,表示该窗口的一对顶点坐标分别为(x1,y1)和(x2,y2)。保证x1<x2,y1<y2。 接下来M行每行包含两个非负整数x,y,表示一次鼠标点击的坐标。题目中涉及到的所有点和矩形的顶点的x,y坐标分别不超过2559和1439。 【输出形式】 输出包括M行,每一行表示一次鼠标点击的结果。如果该次鼠标点击选择了一个窗口,则输出这个窗口的编号(窗口按照输入中的顺序从1编号到N);如果没有,则输出"IGNORED"(不含双引号)。 【样例输入】 3 4 0 0 4 4 1 1 5 5 2 2 6 6 1 1 0 0 4 4 0 5 【样例输出】 2 1 1 IGNORED 【样例说明】 第一次点击的位置同时属于第1和第2个窗口,但是由于第2个窗口在上面,它被选择并且被置于顶层。 第二次点击的位置只属于第1个窗口,因此该次点击选择了此窗口并将其置于顶层。现在的三个窗口的层次关系与初始状态恰好相反了。第三次点击的位置同时属于三个窗口的范围,但是由于现在第1个窗口处于顶层,它被选择。 最后点击的(0,5)不属于任何窗口。 【备注】2014年3月CCF-CSP考试真题第2题 |
//图形窗口问题
#include<iostream>
using namespace std;
typedef struct node{
int bianhao;
int x1,x2,y1,y2;
struct node *next;
}node;
int main()
{
int x,y;
cin>>x>>y;
node *head=NULL,*p;
for(int i=1;i<=x;i++)
{
p=new node;
p->bianhao=i;
cin>>p->x1>>p->y1;
cin>>p->x2>>p->y2;
//头插法
p->next=head;//先做右手动作
head=p;//再做左手动作
}
while(y--)//y次操作
{
int x3,y3;
cin>>x3>>y3;
//查找 从表头开始查找
node *p=head;
while(p!=NULL)
{ //2266 1155 0044 11
if(x3 >= p->x1&&x3<=p->x2&&y3>= p->y1&&y3<=p->y2)
{
cout<<p->bianhao<<endl;
if(p==head) break;//第一个结点即为所求
node *pre=NULL,*q=head;
//两个指针向后平行移动 pre指向p前驱
while(q!=p)
{
pre=q; q=q->next;
}
pre->next=p->next;//断掉
p->next=head;//头插 左手
head=p;//左手
break;
}
else p=p->next;//不符合条件 p后移
}
if(p==NULL) cout<<"IGNORED"<<endl;
}
return 0;
}#include <bits/stdc++.h>
using namespace std;
struct window
{
int x1, y1, x2, y2;
int rank;
};
int main()
{
vector<window> t;
int n,m;
cin >> n>>m;
window w[100];
for (int i = 0; i < n; i++)
{
cin >> w[i].x1 >> w[i].y1 >> w[i].x2 >> w[i].y2;
w[i].rank = i + 1;
t.push_back(w[i]);
}
int x, y;
for (int i = 0; i < m; i++)
{
cin >> x >> y;
int flag = 0;
for (vector<window>::iterator it = t.end() - 1; it >= t.begin(); it--)
{
if ((*it).x1 <= x && (*it).x2 >= x && (*it).y2 >= y && (*it).y1 <= y)
{
cout << (*it).rank << endl;
flag = 1;
window top = *it;
t.erase(it);
t.push_back(top);
break;
}
}
if (flag == 0)
cout << "IGNORED" << endl;
}
}
5.
2.Jungle Roads
| Jungle Roads 请用kruskal算法编程实现下面的问题。 Description
Input The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above. Output The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit. Sample Input 9 A 2 B 12 I 25 B 3 C 10 H 40 I 8 C 2 D 18 G 55 D 1 E 44 E 2 F 60 G 38 F 0 G 1 H 35 H 1 I 35
Sample Output 216 |
#include <bits/stdc++.h>
using namespace std;
struct edgetype
{
int from, to;
int weight;
} edge[2000];
int vexnum, edgenum, res;
int parent[2000];
void creat()
{
cin >> vexnum;
for (int i = 0; i < vexnum - 1; i++)
{
char data;
int num;
cin >> data >> num;
for (int j = 0; j < num; j++)
{
char data2;
int dis;
cin >> data2 >> dis;
edge[edgenum].from = data - 'A';
edge[edgenum].to = data2 - 'A';
edge[edgenum++].weight = dis;
}
}
}
int find(int x)
{
int cur = x;
while (parent[cur] != -1)
{
cur = parent[cur];
}
return cur;
}
int cmp(edgetype a, edgetype b)
{
return a.weight < b.weight;
}
void kruskal()
{
for (int i = 0; i < vexnum; i++)
parent[i] = -1;
sort(edge, edge + edgenum, cmp);
int count = 0;
for (int i = 0; i < edgenum; i++)
{
int a = find(edge[i].from), b = find(edge[i].to);
if (a != b)
{
parent[a] = b;
count++;
res += edge[i].weight;
if (count == vexnum - 1)//连接顶点-1个边 结束
break;
}
}
}
int main()
{
edgenum = 0;
res = 0;
creat();
kruskal();
cout << res;
}
3.迪杰斯特拉最短路径
【问题描述】
在带权有向图G中,给定一个源点v,求从v到G中的其余各顶点的最短路径问题,叫做单源点的最短路径问题。
在常用的单源点最短路径算法中,迪杰斯特拉算法是最为常用的一种,是一种按照路径长度递增的次序产生最短路径的算法。
可将迪杰斯特拉算法描述如下:

在本题中,读入一个有向图的带权邻接矩阵(即数组表示),建立有向图并按照以上描述中的算法求出源点至每一个其它顶点的最短路径长度。
【输入形式】
输入的第一行包含2个正整数n和s,表示图中共有n个顶点,且源点为s。其中n不超过50,s小于n。
以后的n行中每行有n个用空格隔开的整数。对于第i行的第j个整数,如果大于0,则表示第i个顶点有指向第j个顶点的有向边,且权值为对应的整数值;如果这个整数为0,则表示没有i指向j的有向边。当i和j相等的时候,保证对应的整数为0。
【输出形式】
只有一行,共有n-1个整数,表示源点至其它每一个顶点的最短路径长度。如果不存在从源点至相应顶点的路径,输出-1。
请注意行尾输出换行。
【样例输入】
4 1 //这里的1表示第2个顶点,0-1-2-3共计4个顶点,下图为有向图的邻接矩阵。
0 3 0 1
0 0 4 0
2 0 0 0
0 0 1 0
【样例输出】
6 4 7
【样例说明】
在本题中,需要按照题目描述中的算法完成迪杰斯特拉算法,并在计算最短路径的过程中将每个顶点是否可达记录下来,直到求出每个可达顶点的最短路径之后,算法才能够结束。
迪杰斯特拉算法的特点是按照路径长度递增的顺序,依次添加下一条长度最短的边,从而不断构造出相应顶点的最短路径。
另外需要注意的是,在本题中为了更方便的表示顶点间的不可达状态,可以使用一个十分大的值作为标记。
//6. 迪杰斯特拉最短路径
#include <iostream>
const int INF = 9999999;
using namespace std;
int arc[503][503];
int n,start;
int dis[503];
int visit[503] = {0};
int findmin()
{
int min = 2000;
int u = -1;
for (int i = 0; i < n; i++)
{
if (visit[i] == 0 && min > dis[i])
{
min = dis[i];
u = i;
}
}
return u;
}
void show()
{
for (int i = 0; i < n; i++)
{
if (dis[i])
{
if (dis[i] < INF)
cout << dis[i] << " ";
else
cout << -1 << " ";
}
}
}
void dijkstra()
{
int min;
//dis数组初始化
for (int i = 0; i < n; i++)
{
dis[i] = INF;
visit[i] = 0;
}
dis[start] = 0;
for (int i = 0; i < n; i++)
{
int min = findmin();
if (min == -1)
return;
visit[min] = 1;
for (int j = 0; j < n; j++)
{
if (visit[j] == 0 && (arc[min][j] != INF) && dis[j] > dis[min] + arc[min][j])
{
dis[j] = dis[min] + arc[min][j];
}
}
}
}
int main()
{
cin >> n>>start;
int data;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> data;
if (data)
arc[i][j] = data;
else
arc[i][j] = INF;
}
}
dijkstra();
show();
} 弗洛伊德求最短路径【问题描述】 对于下面一张若干个城市,以及城市之间距离的地图,请采用弗洛伊德算法求出所有城市之间的最短路径。
【输入形式】 顶点个数n,以及n*n的邻接矩阵,其中不可达使用9999代替 【输出形式】 每两个顶点之间的最短路径和经过的顶点 注意:顶点自身到自身的dist值为0,path则为该顶点的编号 【样例输入】 4 9999 4 11 9999 6 9999 2 9999 1 9999 9999 1 9999 3 9999 9999 【样例输出】 from 0 to 0: dist = 0 path:0 |
//7. 弗洛伊德求最短路径
#include <bits/stdc++.h>
using namespace std;
const int inf = 9999;
int arc[55][55];
int n;
int dist[55][55];
vector<int> path[55][55];
void floyed()
{
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
dist[i][j] = arc[i][j];
if (dist[i][j] != inf && i != j)
{
path[i][j].push_back(i);
path[i][j].push_back(j);
}
else if (i == j)
path[i][j].push_back(i);
else
path[i][j].push_back(9999);
}
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (dist[i][j] > dist[i][k] + dist[k][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j].clear();
for (int q = 0; q < path[i][k].size() - 1; q++)
{
path[i][j].push_back(path[i][k][q]);
}
for (int q = 0; q < path[k][j].size(); q++)
{
path[i][j].push_back(path[k][j][q]);
}
}
}
void show()
{
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
if (i == j)
{
dist[i][j] = 0;
path[i][j].clear();
path[i][j].push_back(i);
}
cout << "from " << i << " to " << j << ": "
<< "dist = " << dist[i][j] << " path:";
for (int k = 0; k < path[i][j].size(); k++)
{
cout << path[i][j][k] << " ";
}
cout << endl;
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
cin >> arc[i][j];
if (i == j)
arc[i][j] = 0;
}
floyed();
show();
}
欧拉回路
【问题描述】
欧拉回路是指不令笔离开纸面,可画过图中每条边仅一次,且可以回到起点的一条回路。现给定一个图,问是否存在欧拉回路?
本题测试数据不够完善,为检验大家代码的完美度,请自行登陆下面的链接提交。Problem - 1878 (hdu.edu.cn)
【输入形式】
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数,分别是节点数N ( 1 < N < 1000 )和边数M;随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个节点的编号(节点从1到N编号)。当N为0时输入结束。
【输出形式】
每个测试用例的输出占一行,若欧拉回路存在则输出1,否则输出0。
【样例输入】
3 3
1 2
1 3
2 3
3 2
1 2
2 3
0
【样例输出】
1
0
【备注】
此题是浙大计算机研究生复试上机考试-2008年真题。
//8. 欧拉回路
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
int n, m;
while(scanf("%d %d", &n, &m)!=EOF && n!=0)
{
int bian[1000][3] = {0}, ptf=1, same=0;
for(int i=0; i<m; i++){
scanf("%d %d", &bian[i][0], &bian[i][1]);
if(bian[i][0]==bian[i][1]){
bian[i][2]=1;
same++;
}
}
int begin = bian[0][0], end = bian[0][1];
bian[0][2] = 1;
for(int i=1; i<m-same; i++){
int flag=0;
for(int j=0; j<m; j++){
if(bian[j][2]!=1){
if(end==bian[j][0]){
flag=1;
end = bian[j][1];
bian[j][2] = 1;
break;
}
if(end==bian[j][1]){
flag=1;
end = bian[j][0];
bian[j][2] = 1;
break;
}
}
}
if(flag==0){
ptf = 0;
break;
}
}
if(begin==end && ptf) cout<<"1"<<endl;
else cout<<"0"<<endl;
}
return 0;
}
有向无环图的拓扑排序
【问题描述】
由某个集合上的一个偏序得到该集合上的一个全序,这个操作被称为拓扑排序。偏序和全序的定义分别如下:若集合X上的关系R是自反的、反对称的和传递的,则称R是集合X上的偏序关系。设R是集合X上的偏序,如果对每个x,y∈X必有xRy或yRx,则称R是集合X上的全序关系。由偏序定义得到拓扑有序的操作便是拓扑排序。
拓扑排序的流程如下:
1. 在有向图中选一个没有前驱的顶点并且输出之;
2. 从图中删除该顶点和所有以它为尾的弧。
重复上述两步,直至全部顶点均已输出,或者当前图中不存在无前驱的顶点为止。后一种情况则说明有向图中存在环。
采用邻接表存储有向图,并通过栈来暂存所有入度为零的顶点,可以描述拓扑排序的算法如下:

在本题中,读入一个有向图的邻接矩阵(即数组表示),建立有向图并按照以上描述中的算法判断此图是否有回路,如果没有回路则输出拓扑有序的顶点序列。
【输入形式】
输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数0或1,对于第i行的第j个整数,如果为1,则表示第i个顶点有指向第j个顶点的有向边,0表示没有i指向j的有向边。当i和j相等的时候,保证对应的整数为0。
【输出形式】
如果读入的有向图含有回路,请输出“ERROR”,不包括引号。
如果读入的有向图不含有回路,请按照题目描述中的算法依次输出图的拓扑有序序列,每个整数后输出一个空格。
请注意行尾输出换行。
【样例输入】
4
0 1 0 0
0 0 1 0
0 0 0 0
0 0 1 0
【样例输出】
3 0 1 2
【说明】请注意采用邻接表存储结构时,链表创建需采用尾插法,以保证后续结点从小到大排列。
在本题中,需要严格的按照题目描述中的算法进行拓扑排序,并在排序的过程中将顶点依次储存下来,直到最终能够判定有向图中不包含回路之后,才能够进行输出。
另外,为了避免重复检测入度为零的顶点,可以通过一个栈结构维护当前处理过程中入度为零的顶点。
#include <bits/stdc++.h>
#include <iomanip>
using namespace std;
#define Max 1000
#define MVNum 100
#define OK 1
#define ERROR 0
#define OVERFLOW - 2
#define MAXSI 10
typedef int Status;
typedef int SElemType;
typedef int VerTexType;
typedef int OtherInfo;
typedef int ArcType;
typedef struct {
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum, arcnum;
} Graph;
typedef struct {
SElemType *base;
SElemType *top;
int stacksize;
} SqStack;
Status InitStack(SqStack &s)
{
s.base = new SElemType[MAXSI];
if(!s.base)
exit(OVERFLOW);
s.top = s.base;
s.stacksize = MAXSI;
return OK;
}
Status Push(SqStack &s, SElemType e)
{
if(s.top-s.base==s.stacksize)return ERROR;
*s.top=e;
s.top++;
return OK;
}
Status Pop(SqStack &s, SElemType &e)
{
if(s.base==s.top)return ERROR;
s.top--;
e=*s.top;
return OK;
}
bool StackEmpty(SqStack S)
{
if(S.top==S.base)return true;
else return false;
}
void CreateUDG(Graph &g)
{
int i,j;
cin>>g.vexnum;
for(i=0;i<g.vexnum;i++)
{
for(j=0;j<g.vexnum;j++)
{
cin>>g.arcs[i][j];
}
}
}
Status TopSort(Graph g,int topo[])
{
int i,j,m=0,indegree[g.vexnum];
SqStack s;
InitStack(s);
for(i=0;i<g.vexnum;i++)
indegree[i]=0;
for(i=0;i<g.vexnum;i++)
{
for(j=0;j<g.vexnum;j++)
{
indegree[i]=indegree[i]+g.arcs[j][i];
}
}
for(i=0;i<g.vexnum;i++)
{
if(!indegree[i])
{
g.arcs[i][i]=1;
Push(s,i);
}
}
while(!StackEmpty(s))
{
Pop(s,i);
topo[m++]=i;
for(j=0;j<g.vexnum;j++)
{
if(g.arcs[i][j]!=0&&i!=j)
{
g.arcs[i][j]=0;indegree[j]--;
}
if(g.arcs[j][j]==0&&indegree[j]==0)
{
g.arcs[j][j]=1;
Push(s,j);
}
}
}
if(m<g.vexnum)
{
cout<<"ERROR";return 0;
}else
{
for(i=0;i<g.vexnum;i++)
{
cout<<topo[i]<<" ";
}
return 1;
}
}
int main()
{
Graph g;
CreateUDG(g);
int topo[g.vexnum];
TopSort(g,topo);
return 0;
}
拓扑排序和关键路径
【问题描述】若在带权的有向图中,以顶点表示事件,以有向边表示活动,边上的权值表示活动的开销(如该活动持续的时间),则此带权的有向图称为AOE网。如果用AOE网来表示一项工程,那么,仅仅考虑各个子工程之间的优先关系还不够,更多的是关心整个工程完成的最短时间是多少;哪些活动的延期将会影响整个工程的进度,而加速这些活动是否会提高整个工程的效率。因此,通常在AOE网中列出完成预定工程计划所需要进行的活动,每个活动计划完成的时间,要发生哪些事件以及这些事件与活动之间的关系,从而可以确定该项工程是否可行,估算工程完成的时间以及确定哪些活动是影响工程进度的关键。
【输入形式】第一行输入两个数字,分别表示顶点数和边数;从第二行开始,输入边的信息,格式为(i,j, weight)
【输出形式】关键路径的总时间(最大路径长度),代表关键活动的边,格式为(顶点1,顶点2),按大小顺序排列
【样例输入】
6 8
0 1 3
0 2 2
1 3 2
1 4 3
2 3 4
2 5 3
3 5 2
4 5 1
【样例输出】
8
0 2
2 3
3 5
#include<iostream>
#include<string>
using namespace std;
#define MVNum 100
#define OK 1
#define ERROR 0
#define MaxInt 100
typedef string VerTexType;
typedef int Status;
typedef int SElemType;
typedef struct{
SElemType* base;
SElemType* top;
int stacksize;
}SqStack;
typedef struct ArcNode {
int adjvex;
struct ArcNode* nextarc;
}ArcNode;
typedef struct VNode {
VerTexType data;
ArcNode* firstarc;
}VNode,AdjList[MVNum];
typedef struct {
int vexnum, arcnum;
AdjList vertices;
}ALGraph;
/*--------拓扑排序辅助数组的存储结构--------*/
int indegree[MVNum];//存放各顶点入度
int topo[MVNum];//记录拓扑序列的顶点编号
Status InitStack(SqStack& S) {
S.base = new SElemType[MaxInt];
if (!S.base) return ERROR;
S.top = S.base;
S.stacksize = MaxInt;
return OK;
}
Status StackEmpty(SqStack S) {
if (S.top == S.base) return OK;
return ERROR;
}
Status Push(SqStack& S, SElemType e) {
if (S.top - S.base == S.stacksize) return ERROR;
*S.top = e;
S.top++;
return OK;
}
Status Pop(SqStack& S, SElemType& e) {
if (S.base == S.top) return ERROR;
S.top--;
e = *S.top;
return OK;
}
int LocateVex(ALGraph G, VerTexType v) {
for (int i = 0; i < G.vexnum; i++) {
if (G.vertices[i].data == v)
return i;
}
return -1;
}
void CreateUDG(ALGraph& G) {
cin >> G.vexnum >> G.arcnum;
for (int i = 0; i < G.vexnum; i++) {
cin >> G.vertices[i].data;
G.vertices[i].firstarc = NULL;//初始化表头结点的指针域为NULL
}
for (int k = 0; k < G.arcnum; k++) {
VerTexType v1, v2;
cin >> v1 >> v2;
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);
ArcNode* p1 = new ArcNode;
p1->adjvex = j;
p1->nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = p1;
}
}
void FindInDegree(ALGraph G, int indegree[]) {
for (int i = 0; i < G.vexnum; i++) {
int cnt = 0;//设置变量存储邻接点域为i的结点个数
for (int j = 0; j < G.vexnum; j++) {
ArcNode* p = new ArcNode;//定义指向各个边结点的指针
p = G.vertices[j].firstarc;
while (p) {//当p未指到单个链表的末尾时继续循环
if (p->adjvex == i)//当某边结点邻接点域等于i时,计数变量++
cnt++;
p = p->nextarc;//指针不断向后指
}
indegree[i] = cnt;//将计数结果保留在indegree数组中
}
}
}
Status TopologicalSort(ALGraph G, int topo[]) {
//有向图G采用邻接表存储结构
//若G无回路,则生成G的一个拓扑排序topo[]并返回OK,否则ERROR
FindInDegree(G, indegree);//求出各结点的入度存入数组indegree中
SqStack S;
InitStack(S);//初始化栈
for (int i = 0; i < G.vexnum; i++) {
if (!indegree[i]) Push(S, i);//入度为0者进栈
}
int m = 0;//对输出顶点计数u,初始为0
while (!StackEmpty(S)) {
int i = 0;
Pop(S, i);//将栈顶顶点vi出栈
topo[m] = i;//将vi保存在拓扑序列数组topo中
++m;//对输出顶点计数
ArcNode* p = new ArcNode;
p = G.vertices[i].firstarc;//p指向vi的第一个邻接点
while (p != NULL) {
int k = p->adjvex;//vk为vi的邻接点
--indegree[k];//vi的每个邻接点的入度减一
if (indegree[k] == 0) Push(S, k);//若入度减为0,则入栈
p = p->nextarc;//p指向顶点vi下一个邻接结点
}
}
if (m < G.vexnum) return ERROR;//该有向图有回路
else return OK;
}
/*输出拓扑排序后的结果*/
void PrintResult(ALGraph G) {
if (TopologicalSort(G, topo)) {
for (int i = 0; i < G.vexnum; i++) {
cout << G.vertices[topo[i]].data << " ";
}
}
}
int main() {
ALGraph G;
CreateUDG(G);
PrintResult(G);
return 0;
}
6 8
v1 v2 v3 v4 v5 v6
v1 v2
v1 v3
v1 v4
v3 v2
v3 v5
v4 v5
v6 v4
v6 v5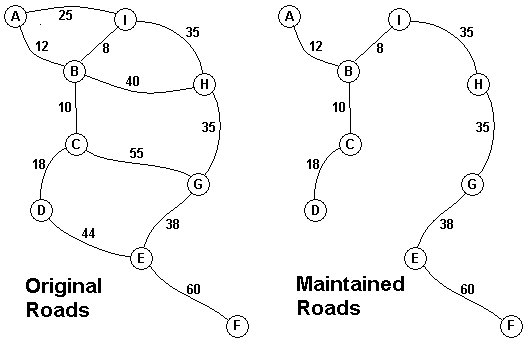






![Termius使用[分屏同时操作]](https://img-blog.csdnimg.cn/8e12657597904428a5b7e23a357b919d.png)