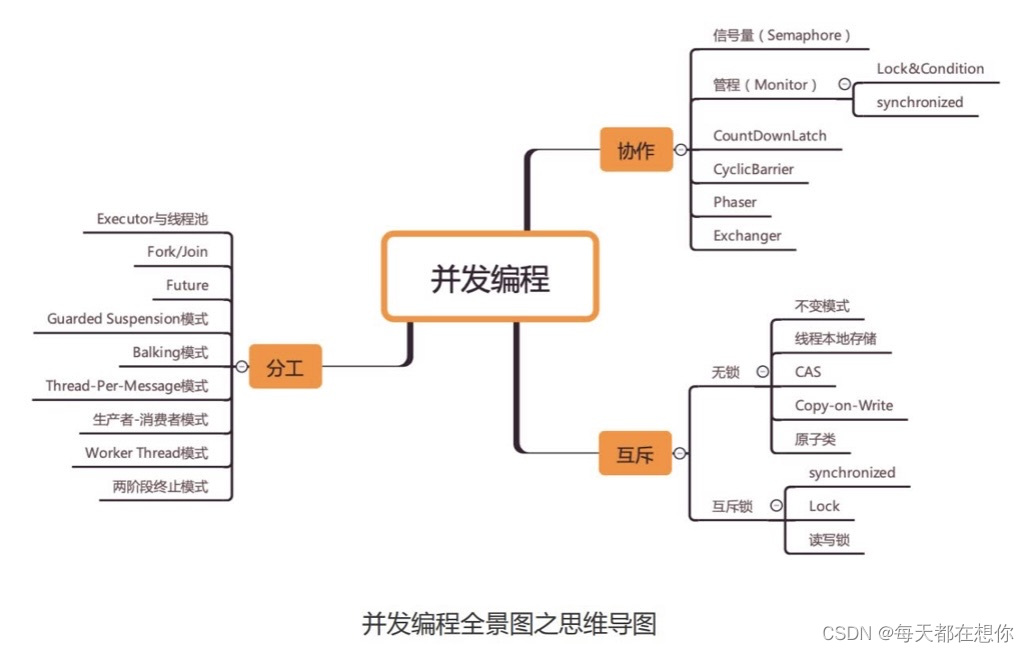
softmax的基本概念


交叉熵损失函数

模型训练和预测
在训练好softmax回归模型后,给定任一样本特征,就可以预测每个输出类别的概率。通常,我们把预测概率最大的类别作为输出类别。如果它与真实类别(标签)一致,说明这次预测是正确的。
代码
- 导入相关库
import torch
from torch import nn
- 定义数据集
自定义输入X为7张高和宽均为2像素的灰度图片
自定义输出target为 y1=0, y2=1 , y3=2
# 确定随机数种子
torch.manual_seed(7)
# 自定义数据集
X = torch.rand((7, 2, 2))
target = torch.randint(0, 2, (7,))
- 定义网络结构
定义如下所示的网络结构

# 自定义网络结构
class LinearNet(nn.Module):
def __init__(self):
super(LinearNet, self).__init__()
# 定义一层全连接层
self.dense = nn.Linear(4, 3)
# 定义Softmax
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
y = self.dense(x.view((-1, 4)))
y = self.softmax(y)
return y
net = LinearNet()
- 定义损失函数
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction=‘mean’)
衡量模型输出与真实标签的差异,在分类时相当有用。
结合了nn.LogSoftmax()和nn.NLLLoss()两个函数,进行交叉熵计算。
主要参数:
weight: 各类别的loss设置权值
ignore_index: 忽略某个类别
reduction: 计算模式,可为none/sum/mean
none: 逐个元素计算
sum: 所有元素求和,返回标量
mean: 加权平均,返回标量
loss = nn.CrossEntropyLoss() # 交叉熵损失函数
- 定义优化函数
torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)
构建一个优化器对象optimizer,用来保存当前的状态,并能够根据计算得到的梯度来更新参数,使得模型输出更接近真实标签。
学习率(learning rate)控制更新的步伐。
主要参数:
params: 管理的参数组
lr: 初始化学习率
momentum: 动量系数
weight_decay: L2正则化系数
nesterov: 是否采用NAG
zero_grad(): 清空所管理参数的梯度,因为Pytorch张量梯度不自动清零。
step(): 执行一步更新
optimizer = torch.optim.SGD(net.parameters(), lr=0.1) # 随机梯度下降法
- 开始训练模型
for epoch in range(70):
train_l = 0.0
y_hat = net(X)
l = loss(y_hat, target).sum()
# 梯度清零
optimizer.zero_grad()
# 自动求导梯度
l.backward()
# 利用优化函数调整所有权重参数
optimizer.step()
train_l += l
print('epoch %d, loss %.4f' % (epoch + 1, train_l))