找到 FSM 的区别序列、UIO 或特征集(W方法)

1 简介
许多系统都是基于状态的：它们有一个更新的内部状态通过操作并影响行为。 在测试这样一个系统时，一个需要考虑状态。 这导致了一系列的语言，用于描述基于状态的规范和模型，这些可以在许多应用领域。 比如嵌入式的开发汽车和航空电子工业中的控制系统通常使用以状态图形式编写的基于状态的模型。
如果我们有一个基于状态的模型，那么就有可能利用这在测试中。 例如，我们可以考虑覆盖率的简单概念（例如执行转换的比例），此外，如果我们可以提供一个具有形式语义的模型，然后我们可以以此为基础用于自动化部分测试。
标准方法之一是表示作为有限状态机或标记转换的模型的语义系统。
在本课程中，我们将重点介绍有限状态机。使用有限状态机 (FSM) 对系统建模已导致许多有兴趣从中得出测试。 最初，这项工作最初的动机主要是测试硬件（处理器）和实现的问题通信协议，但现在有更广泛的兴趣。 得出来自 FSM 的测试序列，应用于被测系统 (SUT)并将测试输出与预期进行比较。
在课程的这一部分结束时，您应该能够：
• 定义一个有限状态机并解释它是如何运作的
• 定义和解释与有限状态机相关的术语的相关性
• 查找序列以达到或区分状态
• 找到 FSM 的区别序列、UIO 或特征集
• 从 FSM 生成过渡游览
• 应用 W 方法

2 有限状态机
有限状态机（也称为 Mealy 机）M 由tuple组定义(S, s0, δ, λ,X,Y ) 其中 S 是状态的有限集，s0 是初始状态，δ是状态传递函数，λ是输出函数，X是有限输入字母表，Y 是有限输出字母表。 如果 M 接收到输入 x 时,在状态 si 中，它移动到状态 sj = δ(s, x) 并产生输出 y = λ(s, x)。这定义了转换 (si, sj,x/y)。 请注意，形式化确保我们认为 FSM 是确定性的； 还有一些测试方法非确定性 FSM，但我们不会在本课程中考虑它们。

FSM 可以用有向图表示，其中状态由顶点表示，转移 (si, sj, x/y) 由从标记为 si 的顶点到标记为 sj 的顶点的边表示，该边具有标签 x/y。

• “x”：它表示触发从状态 si 到状态 sj 的转换的一个或多个输入符号。 当 FSM 接收到与“x”匹配的输入符号或序列时，它将从状态 si 转换到状态 sj。
• “y”：它表示 FSM 在从状态 si 到状态 sj 的转换过程中产生的一个或多个输出符号。 当 FSM 进行转换时，它可以生成对应于“y”的输出符号或序列。

通过在所描述的 FSM 表示中包含标签“x/y”，它提供了有关与每个转换相关的输入和输出的信息。 这种表示法可以更详细、更明确地表示 FSM 的行为，从而更好地理解状态和转换的连接方式以及输入和输出的处理方式。

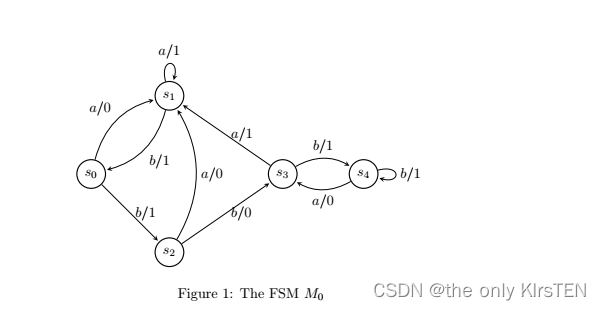
例如，Figure 1 表示我们将称为 M0 的 FSM。 例如，在这个 FSM 中，有一条边从标号为 s2 的顶点到标号为 s3 的顶点，这条边的标号为 b/0。 这表示转换 (s2, s3, b/0)并告诉我们，如果此 FSM 在状态 s2 中接收到输入 b，则它输出 0 并移动到 s3。
考虑 M0 的行为。 如果 M0 接收到输入 abbb，当处于初始状态 s0 时，我们得到以下内容：

1. 初始输入 a 触发转换 (s0, s1, a/0)，因此 M0 输出 0 并移动到状态 s1。
2. 第二个输入 b 现在触发转换 (s1, s0, b/1)，因此 M0 输出并返回到状态 s0。
3. 当 M0 处于状态 s0 时，现在接收到第三个输入 b，因此它触发转换 (s0, s2, b/1)。 因此 M0 输出 1 并移动到状态 s2。
4. 当 M0 处于状态 s2 并触发转换（s2,s3,b/0）。 因此，M0 输出 0 并移动到状态 s3

结果，abbb的输入导致路径 (s0, s1, a/0)(s1, s0, b/1)(s0, s2, b/1)(s2,s3,b/0)
因此在 M0 的初始状态下 abbb 的输入将 M0 带到状态 s3 并输出 0110。这给出了可以表示的轨迹（输入/输出序列）
作为 a/0 b/1 b/1 b/0 或 abbb/0110

3 FSM 的类型和 FSM 的性质properties
我们将专注于特定类型的 FSM。
如果没有成对的转换具有相同的初始状态和输入，则 FSM 被认为是确定性的。 这隐含在上面的定义中，因为 δ 和 λ 是函数（在每种情况下，只给出一个允许值状态和输入）。 我们将只考虑确定性 FSM。
如果对于每个输入 x 和每个状态 si，M 中存在从具有输入 x 的 si 的转换，则称 FSM M 是完全指定的。 如果 FSM M 未完全指定，则可以通过应用以下方法之一从 M 生成完全指定的 FSM M 0：
• 添加错误状态。 对于每个具有 si 和 x 的 (si; x)，这样没有从 si 到输入 x 的转换，我们添加一个从 si 到错误状态的输入 x 的转换，并使此转换的输出是一些错误消息。
• 添加空动作。 对于每个 (si; x)，对于 si 和 x ，这样没有从 si 到输入 x 的转换，我们添加一个从 si 到 si 的输入 x 的转换，并使该转换的输出为空。
第一种方法对应于输入 x 没有指定行为的情况，状态 si 意味着系统在状态 si 时不应接收 x，因此这应该导致错误消息或引发异常。 第二种情况对应于输入 x 没有指定行为的假设，状态 si 意味着在状态 si 中 x 的输入没有效果。
由于 λ 和 δ 是（总）函数，我们的形式主义只允许我们描述完全指定的确定性 FSM。 放宽这些限制并不难，但我们将重点关注此类 FSM（确定性和完全指定的）。

如果 M 的每个状态都可以从 M 的初始状态到达，则 FSM M 是初始连接的：对于 M 的每个状态 s，存在一些输入序列 x¯ 使得 s = λ∗(s0; x¯)。 如果存在无法从初始状态到达的状态 s，则可以删除 s，因为它对 M 的指定行为没有贡献。因此，我们可以假设所考虑的任何 FSM 都是初始连接的。 FSM M 是强连通的，如果给定任何有序的状态对 (si, sj)，则有是将 M 从 si 移动到 sj 的一系列转换。
重置是将 M 带入其初始状态的输入，而不管当前状态如何。 许多真实系统都有重置操作； 有时这只是表示关闭系统然后再打开。 多项测试技术假设存在可靠的重置：已知已正确实施的重置。
显然，如果 M 有一个重置并且是初始连接的，那么它也是强连接的。 由于大多数系统都有一些重置，许多技术假设所考虑的任何 FSM 都是强连接的。 很容易确认 M0 是强连接。 例如，为了从初始状态到达状态 s4，使用输入序列 bbb 就足够了，然后我们可以通过应用 aab 返回到初始状态。

如果状态 si 和 sj 中的 x¯ 输入导致不同的输出序列 (λ^∗(si, x¯) /= λ ^∗)，则称 FSM M 的两个状态 si 和 sj 被输入序列 x¯ 分开 (sj, x¯))。 本质上这意味着，如果您知道实现当前处于状态 si 或 sj，那么为了确定当前状态，输入 x¯ 并观察输出就足够了。

如果 FSM M 的两个状态不能分开，则称它们是等价的。这恰好是从每个状态产生同一组输入/输出序列的时候。 如果两个 FSM 的初始状态是等价的，则它们是等价的。 一个
如果不存在具有更少状态的等效 FSM，则 FSM M 被称为最小的。如果 M 是初始连接的，则如果 M 没有一对等效状态，则 M 是最小的。 比较容易检查状态 M0 中没有两个是等价的，并且
所以 M0 是最小的。 如果 FSM 不是最小的，则可以将其转换为等效的最小 FSM，这可以在多项式时间内通过使用用于最小化确定性有限自动机的标准算法来实现。
总而言之，我们假设所考虑的任何 FSM 是：
• 确定性。
• 完全指定。
• 最小（这也意味着它是初始连接的）。

4 故障及过渡游览法
当从 FSM M 进行测试时，通常假设 SUT 的行为类似于某个未知的 FSM MI，它具有与 M 相同的输入和输出字母表。因此，测试涉及比较两个 FSM 的行为。 其中一个 FSM 是未知的，它就像一个黑盒子。 我们也可以假设 MI 对于某个预先确定的 m 最多有 m 个状态。
转换中的错误可归类为以下一项或多项：
• 输出故障：转换有错误的输出
• 状态转移故障：转移将M带到错误的状态。

当然，由于状态转移错误，也可能存在额外的状态。
不同的测试技术在它们寻找的故障类型和它们假定的规范属性方面有所不同。 在本节中，我们将重点关注查找输出故障的问题，并基本上假设没有状态传输故障。
如果我们假设只存在输出故障，那么产生一些测试序列或一组测试序列就足够了，这些测试序列执行 M 的每个转换。如果只有一个测试序列，那么我们将其称为转换之旅。 例如，
以下是M0的transition tour（不是唯一的transfer tour）

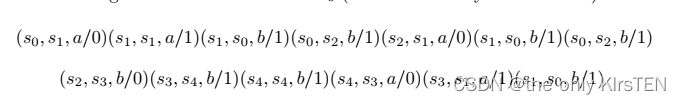
沿着这条通过 M0 的路径，可以确认它通过了每条边，因此包括了每一个转换。 此路径导致以下测试序列：

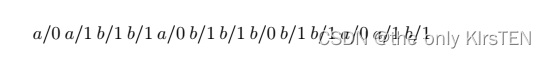
自然地，在可能存在状态转移错误的地方，通常认为转换之旅是不够的。 事实上，在可能存在状态转移故障的情况下，甚至不能保证转换巡回检测到每个输出故障：状态转移故障可能会掩盖此类输出故障。

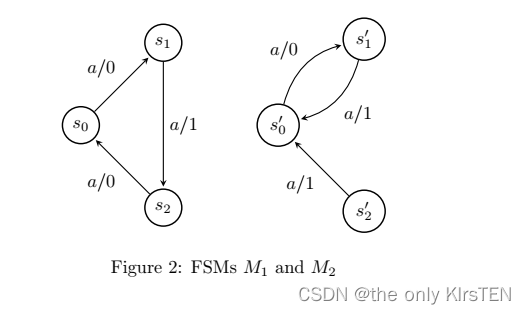
Figure 2 给出了一个例子。 这里的规范是 M1，SUT 是 M2。 SUT 包含一个输出故障（在从 s2 的转换中），由于从 s1 的转换中的状态转移故障，转换巡回 aaa 未检测到。 要查看 M2 是否有故障，请考虑其对输入 aaaa 的响应以及规范 M1 对 aaaa 的响应。

5 识别状态和发现状态转移错误
从 FSM 进行的测试通常可以看作是检查 SUT 的转换与 FSM 的转换的过程。 为了检查转换 t = (si, sj, x/y) 我们需要输入一个序列以移动到状态 si，输入值 x（检查 y 是否输出）然后检查状态现在是 si。 如果我们希望能够找到状态转移错误，则需要最后一部分。
根据 FSM 规范进行的测试通常是黑盒测试：测试人员看不到实现的实际状态。 这会导致另外两个问题：
• 可控性Controllability：当测试从状态 s 的转换时，有必要应用将实现带到相应状态的输入序列
• 可观察性Observability：当测试从状态si 到状态sj 的转换时，有必要检查转换后SUT 的状态是否正确。

可控性问题已经讨论过了。 为了克服可观察性问题，能够通过提供进一步的输入并观察产生的输出来检查 IUT 的状态就足够了。 因此，为了测试一个转换，有必要有一些方法来检查它的最终状态。 存在三种检查状态的主要方法。 这些基于：
• 区别序列Distinguishing sequence (DS)
• 独特的输入/输出序列Unique Input/Output sequences （UIO）
• 特征集Characterising set

IUT 代表测试中的实现。 它是指在特定场景或实验中被测试的系统或软件。 IUT 的“状态”指的是测试过程中给定时间点系统的当前状况或配置。 它包括变量值、组件或模块的状态以及描述系统行为或特征的任何其他相关信息等因素。
在克服可观察性问题时，检查 IUT 的状态意味着通过提供额外的输入并观察相应的输出来收集有关其内部工作和输出的信息。 这使测试人员或研究人员能够深入了解系统的运作方式，并根据预期或期望的结果验证其行为。 通过检查 IUT 的状态，可以评估其正确性、性能、可靠性或任何其他感兴趣的属性。

区别序列是为每个状态产生不同输出的输入序列。 因此，当输入区分序列 D 时，响应于此产生的输出标识系统在输入 D 之前所处的状态。
给定一个可区分序列 D，为了检查转移 t，我们在其后跟 D。因此，如果我们希望使用可区分序列 D 来检查转移 t = (si, sj, x/y) 的结束状态，那么它足以开始将 M 带到 si 的输入序列，然后应用输入 x，最后应用 D 来检查到达的状态是否为 sj。

并非所有的 FSM 都有可区分的序列。 例如，可以证明 M0 没有区分序列。 要了解这一点，请考虑两种情况。
• 考虑以a 开头的输入序列。 这些无法形成可区分的序列，因为在状态 s1 和 s3 中输入 a 会导致公共输出 (1) 并且到达相同的状态 (s1)。
• 考虑以b 开头的输入序列。 这些不能形成可区分的序列，因为状态 s3 和 s4 中的 b 的输入导致共同的输出 (1) 并且到达相同的状态 (s4)。
另一种方法是使用唯一的输入/输出序列，其中输入/输出序列 x¯ =y¯ 是状态 si 的唯一输入/输出序列 (UIO)，如果满足以下条件：
y¯ 是在状态 si ( y¯ = λ^∗ (si, x¯)) 下输入 x¯ 时产生的输出；
对于所有 sj /= si，我们有 λ^∗ (sj, x¯) /= y¯

因此 x¯ 将 si 与 M 的所有其他状态分开，并且 y¯ 响应 x¯ 的输出验证状态是 si。 虽然 x¯ 可以验证 si 它不需要能够验证任何其他状态。 因此，在测试转换 t 时，我们通过 UIO 跟随它以获得 t 的最终状态。 显然，DS 是每个状态的 UIO，并且不难证明存在具有所有状态的 UIO 但没有 DS 的 FSM。 但是请注意，上面的论点表明 M0 没有 UIO

如果状态 S2 有一个输入 ‘a’ 和输出 ‘1’ 的自循环，那么只要在有限状态机中有一个唯一的输入序列可以用来区分 S2 和其他状态，UIO 属性仍然成立 （有限状态机）。

对于状态 s3。 虽然没有有效的算法来确定 FSM 是否具有所有状态的 UIO，但如果 FSM 不是太大，那么我们可以简单地使用广度优先搜索breadth-first search，如果我们确定以下情况，则该过程可以变得更有效 给定的输入序列不能扩展为正在考虑的状态形成 UIO。

广度优先搜索（Breadth-First Search，简称BFS）是一种用于图或树的遍历算法。它从给定的起始节点开始，逐层地向外探索图的结点，直到找到目标节点或遍历完整个图。BFS 以广度优先的方式遍历图的节点，即先访问离起始节点最近的节点，然后再逐渐扩展到离起始节点更远的节点。
BFS 的基本思想是使用队列（Queue）数据结构来保存待访问的节点。算法从起始节点开始，将其加入队列，然后依次从队列中取出节点进行访问。对于每个被访问的节点，将其所有未访问的相邻节点加入队列，然后标记这些相邻节点为已访问。这样，BFS 会逐层遍历图的节点，确保先访问离起始节点最近的节点。

一些 FSM 没有针对每个状态的 DS 或 UIO。
在一些特殊的情况下，一些 FSM（有限状态机）可能没有针对每个状态的可区分序列（DS）或唯一输入/输出序列（UIO）。这通常是由于FSM的特定结构或行为导致的。
以下是一些可能导致 FSM 没有 DS 或 UIO 的情况：

1. 非确定性状态机（Non-Deterministic Finite State Machine，NFSM）：NFSM 允许在某个状态下具有多个可能的转移选项，而不是唯一确定的转移。这种非确定性可以导致在某些情况下无法找到针对每个状态的可区分序列或唯一输入/输出序列。

2. 循环状态机（Cyclic Finite State Machine）：如果 FSM 包含循环或环路，并且没有其他转移路径可以将其退出循环，那么可能很难找到针对循环内部状态的可区分序列或唯一输入/输出序列。在这种情况下，循环可能会导致无法确定当前状态的唯一标识。

3. 部分可观测状态机（Partial Observable Finite State Machine）：在一些情况下，FSM 的输出可能不完全可观测，即无法准确地确定当前状态。这可能是由于输出受限、存在噪声或其他因素导致的。在这种情况下，即使存在针对每个状态的可区分序列，也无法完全观测到输出以唯一地确定状态。

这些是一些可能导致 FSM 没有针对每个状态的可区分序列或唯一输入/输出序列的情况。根据 FSM 的特性和行为，可能需要采用其他测试方法或技术来分析和验证 FSM 的行为。

然而，每个最小 FSM 都有一个特征集。 特征集是一组 W 的输入序列，其属性是，如果每个序列都从某个状态 si 执行，则输出序列集会验证 si。 更正式地说，W 是一个特征集，如果对于每对状态 si, sj 和 si /= sj, 有一些输入序列 x¯ 属于将 si 和 sj 分开的 W（即 λ∗(si, x¯) /= λ∗(sj, x¯)）。 当使用特征集 W 检查转换 t = (si, sj,x=/y) 时，我们需要分别在 t 后面跟从 W 中的每个元素。
存在用于生成特征集的有效（多项式时间）算法。 此外，如果 M 是具有 n 个状态的最小 FSM，则它必须具有最多包含 n − 1 个序列的特征集，每个序列的长度最多为 n − 1。以下给出了每个状态对 a 和 bbb 的响应 M0。 由于行都不同，我们知道 {a, bbb} 是 M0 的特征集。

6 W方法
我们现在将描述 W 方法，它产生一个检查实验：一组输入序列，在它们之间，只要 SUT 表现得像一些（未知的）FSM 具有与 M 相同的输入字母表并且没有 超过 m 个状态（一些预先确定的 m）。 产生的序列由重置分开，因此该方法依赖于可靠重置操作的存在。

W 方法使用特征集 W 和状态覆盖 V，其中 V 是状态覆盖，如果它是一组具有以下属性的输入序列： M 的每个状态都由 V 和 V 的序列从 s0 到达 包含输入空序列。 自然地，这个状态覆盖通常会有多个选择，但可以使用广度优先搜索找到最小状态覆盖。
考虑我们的示例 M0，一种可能的状态覆盖：{ , a,b, bb,bbb}，其中 表示空序列。 在这里，例如，状态 s3 由 bb 到达。 如前所述，一种可能的特征集是 W = {a, bbb}。
假设表示 SUT 行为的 FSM MI 的状态不超过 M（因此 m = n），W 方法产生以下测试：

在给定的示例中，特征集表示为 W = (a, bbb)。 W 中的每个符号对应于要应用于被测 FSM (SUT) 的输入序列。

现在，让我们分解序列 V W U V X W：

V：这表示要应用于 FSM 的输入序列 V。
W：然后将特征集 W = (a, bbb) 应用于 FSM。 在这种情况下，输入“a”和“bbb”按顺序应用。
V：输入序列 V 再次应用于 FSM。
X：这表示要应用于 FSM 的不同输入序列 X。
W：再次将特征集 W = (a, bbb) 应用于 FSM。

因此，序列 VWUVXW 表示要在 FSM 上执行的输入动作序列。 具体来说，它涉及应用输入序列 V、‘a’、‘bbb’、V、X，然后再次应用特征集 W = (a, bbb)。

每个输入序列（V、U、X）的具体含义和目的取决于上下文和被测试的特定 FSM。 这些输入序列的解释通常会在特定系统或正在考虑的 FSM 的测试过程的上下文中定义。

我们可以将这两个术语视为执行不同的角色。 如果 SUT 通过了 VW 中的测试，那么我们就知道关于 SUT 的以下两个事实。
• 输入序列的集合V达到MI的n个不同状态，因为在V中的不同输入序列之后必然对W有不同的响应（因为在规范M中就是这种情况，规范和SUT产生相同的输入/输出 响应 V W 的序列）。 因此，由于 MI 最多有 n 个状态，因此 V 也必须是 MI 的状态覆盖。
• 集合W 成对区分V 达到的SUT 的n 个状态。 结果，由于 MI 最多有 n 个状态，W 也必须是 MI 的特征集。
结果，集合 V XW 检查了 MI 的所有转换。 其中 m > n，W 方法生成以下测试集：


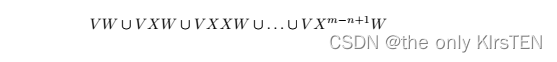
在给定的上下文中，变量 m 和 n 用于表示有限状态机 (FSM) 中的状态数。

在语句“m = n + 3”中，它表明被测 FSM (SUT) 有 m 个状态，并且它比另一个由 n 个状态表示的 FSM 多三个状态。
进一步澄清：

• n 表示参考 FSM 中的状态数，表示为 MI，作为比较的基础。
• m 表示被测 FSM 中的状态数，记为 SUT。

例如，如果 m = n + 3，则表示 SUT 比参考 FSM MI 多了三个状态。 m 和 n 的具体值将取决于上下文和所考虑的特定 FSM。

请务必注意，m 和 n 的值以及与其关系相关的特定条件或假设可能会因所讨论的特定场景、问题或测试方法而异。