---

题目

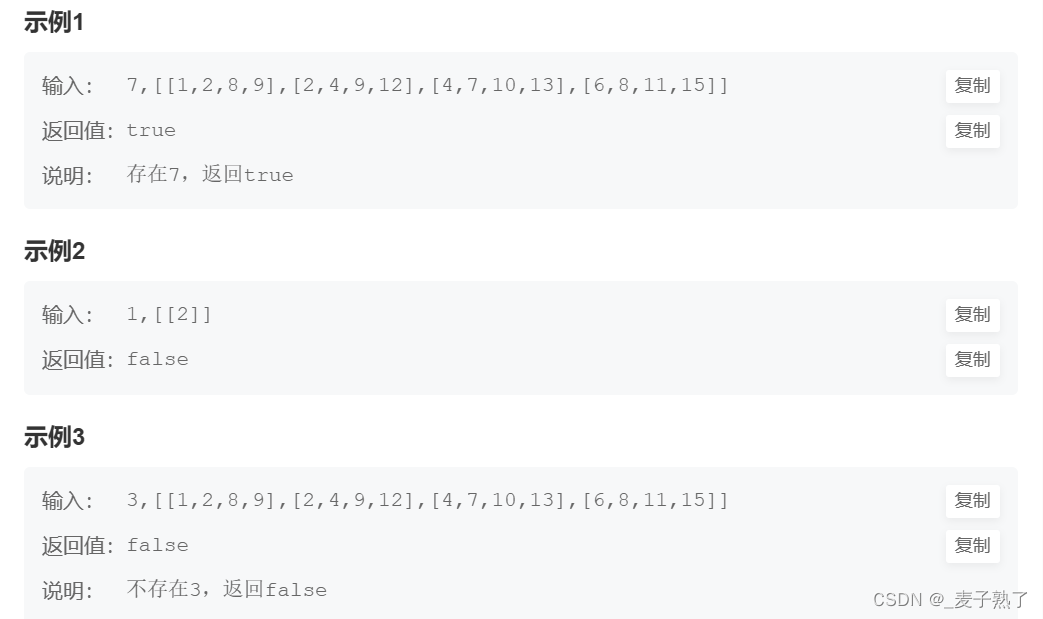
题目链接入口：牛客：JZ4 二维数组中的查找

思路

1.核心考点

（1） 数组相关：二维数组（矩阵）。
（2） 特性观察：在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。
（3） 时间复杂度的把握：O(m+n)，遍历矩阵的时候，最多经过矩阵的一行一列。
（4） 空间复杂度的把握：O(1)，常数级变量，无额外辅助空间。
2.解题思路

1. 查找的过程，本质是排除的过程。那么一次排除一个和一次排除一批，当然是后者的效率更高。暴力查找算法，即遍历整个二维矩阵，是一次排除一个的做法，可以解决这个问题，但是效率低，并且没有利用到题目给出的特性，所以不介意这种做法。
2. 下面给出了一个矩阵样式的图，我们以这个矩阵为例。通过观察，右上角的元素4，是它这一行的最大值，是它这一列的最小值；或者左下角的元素3，是它这一行的最小值，是它这一列的最大值。这是解决这道题的关键突破口。
   
   3.如何解决？
   如果要找的值小于右上角（4），则排除这一列（排除了4,5,6），因为右上角的值是这一列最小的，如果我们要找的值还小于4，那么肯定不在这一列;

如果我们要找的值大于右上角，则排除这一行（排除了1,2，3,4），因为右上角元素是这一行最大的，如果我们要找的值还大于4，那么肯定不在这一行。

4.排除一行，或一列后，剩下的元素还是一个二维数组，所以我们可以复用这个方法。

5.临界条件：i表示行，j表示列。以右上角为基准值，保证i,j在二维数组的合法范围即可。

6.总结：这种方法，一次可以排除一行，或者一列，相比暴力查找算法（一次只排除一个），效率高太多了，还有比如二分查找算法，它是一次可以排除一半，当然它的条件是有序，所以它的效率也超高。

代码实现

C++版本：

class Solution {
public:
    bool Find(int target, vector<vector<int> > array) {
        //我们以最右上角的元素为例
        int i=0;
        int j=array[0].size()-1;

        //临界条件
        while(i<array.size()&&j>=0)
        {
            if(target<array[i][j])array[i][j]一定是当前行最大的，当前列最小的
            {
                j--;//排除这一列
            }
            else if(target>array[i][j])
            {
                i++;//排除这一行
            }
            else {
                //找到了
                return true;
            }
        }
        return false;
    }
};

java版本：

public class Solution {
    public boolean Find(int target, int [][] array) {
        if (array == null) {
            return false;
        }
        int i = 0;
        int j = array[0].length - 1;
        while ( i < array.length && j >= 0) {
            if (target <array[i][j]) { //array[i][j]一定是当前行最大的，当前列最小的
                //target < array[i][j] 排除当前列
                j--;
            }
            else if (target > array[i][j]) {
                //target > array[i][j] 排除当前行
                i++;
                
            }
            else {
                //找到
                return true;
            }
        }
        return false;
    }
}