【数据结构】---几分钟简单几步学会手撕链式二叉树(下)

news2024/12/28 5:57:51

文章目录

  • 前言
  • 🌟一、二叉树链式结构的实现
    • 🌏1.1 二叉树叶子节点个数
      • 💫代码：
      • 💫流程图：
    • 🌏1.2 二叉树的高度
      • 💫第一种写法(不支持)：
          • 📒代码：
          • 📒流程图：
      • 💫第二种写法：
          • 📒代码：
          • 📒流程图：
    • 🌏1.3 二叉树第K层的节点个数
      • 💫代码：
      • 💫流程图：
    • 🌏1.4 二叉树查找值为x的节点
      • 💫第一种写法(错误示范)：
          • 📒代码：
          • 📒流程图：
      • 💫第二种写法(正确写法)：
          • 📒代码：
          • 📒流程图：
    • 🌏1.5 层序遍历
          • 📒代码：
          • 📒思路流程(多种嵌套)：
    • 🌏1.6 二叉树销毁(采用后序)
          • 📒代码：
          • 📒流程图：
    • 🌏1.7 判断二叉树是否是完全二叉树
          • 📒代码：
          • 📒思路流程：
  • 🌟二、二叉树链式结构完整代码
  • 😽总结

前言

👧个人主页：@小沈熬夜秃头中୧⍤⃝❅
😚小编介绍：欢迎来到我的乱七八糟小星球🌝
📋专栏：数据结构
🔑本章内容：手撕链式二叉树
送给各位💌：成为更好的自己才是应该做的事
记得 评论📝 +点赞👍 +收藏😽 +关注💞哦~

提示：以下是本篇文章正文内容，下面案例可供参考

🌟一、二叉树链式结构的实现

🌏1.1 二叉树叶子节点个数

💫代码：

int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

💫流程图：

在这里插入图片描述

🌏1.2 二叉树的高度

💫第一种写法(不支持)：

📒代码：
int BTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	return BTreeHeight(root->left) > BTreeHeight(root->right) ?
		BTreeHeight(root->left) + 1 : BTreeHeight(root->right) + 1;
}
📒流程图：

由图可知，每次比较完后并没有记录数据而是再次调用当树跃高底层最大的那个函数调用的次数就越多，所以这种方法虽然对但是耗时太长，而底层也就变成了所谓的天选打工人在这里插入图片描述

💫第二种写法：

📒代码：
int BTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int leftHeight = BTreeHeight(root->left);
	int rightHeight = BTreeHeight(root->right );
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
📒流程图：

每次调用都记录上数据，这样比较完直接返回大的那个+1；在这里插入图片描述

🌏1.3 二叉树第K层的节点个数

💫代码：

int BTreeLevelKSize(BTNode* root,int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BTreeLevelKSize(root->left, k - 1) 
		+ BTreeLevelKSize(root->right, k - 1);
}

💫流程图：

在这里插入图片描述
在这里插入图片描述

🌏1.4 二叉树查找值为x的节点

💫第一种写法(错误示范)：

📒代码：
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data  == x)
		return root;
	BTreeFind(root->left, x);
	BTreeFind(root->right, x);
}
📒流程图：

在这里插入图片描述

💫第二种写法(正确写法)：

📒代码：
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data  == x)
		return root;
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1)
		return ret1;
	BTNode* ret2 = BTreeFind(root->left, x);
	if (ret2)
		return ret2;
	return NULL;
}
📒流程图：

在这里插入图片描述

🌏1.5 层序遍历

📒代码：
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	printf("\n");
	QueueDestroy(&q);
}
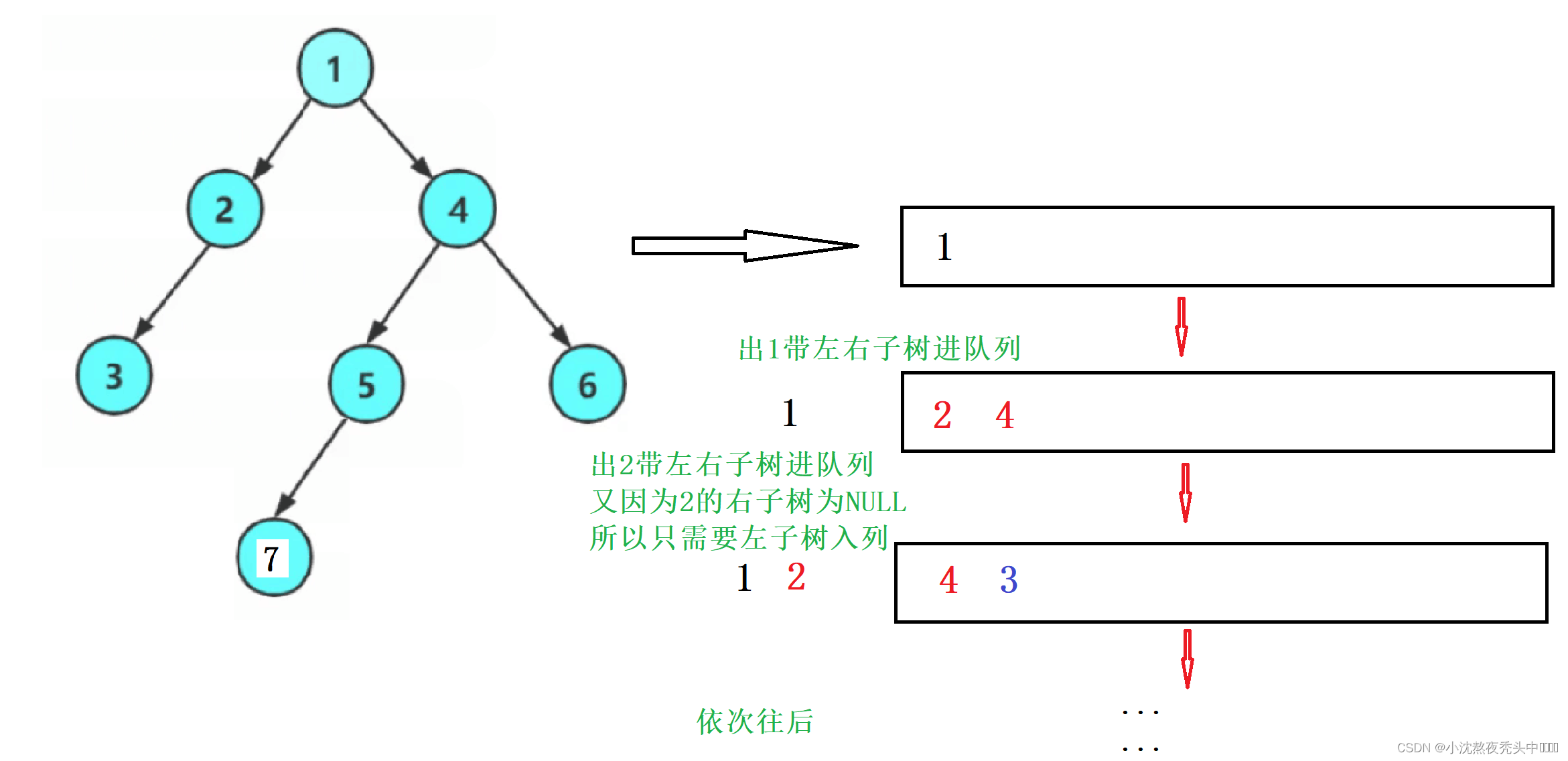
📒思路流程(多种嵌套)：

对于层序遍历,可以采用队列的思想(先进先出)
具体核心思想：上一层出时带下一层进队列所以进入时不能存储树节点的值而是存储树节点指针
请添加图片描述
在这里插入图片描述

🌏1.6 二叉树销毁(采用后序)

📒代码：
void BTreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;
	BTreeDestroy(root->left);
	BTreeDestroy(root->right);
	free(root);
}
📒流程图：

在这里插入图片描述

🌏1.7 判断二叉树是否是完全二叉树

📒代码：
bool BTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//遇到空就跳出
		if (front == NULL)
			break;

		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	//检查后面的节点有没有非空
	//有非空不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)//往外拿数出现非空就不是完全二叉树
		{
			return false;
			QueueDestroy(&q);
		}
	}
	return true;
	QueueDestroy(&q);
}
📒思路流程：

和上述层序遍历一样，采用队列思想，上一层出时带下一层进入，出现NULL时跳出然后将里面的数字往外拿，出现非空不是完全二叉树请添加图片描述>N代表空在这里插入图片描述

🌟二、二叉树链式结构完整代码

//Queue.h
#pragma once
#include<assert.h>
#include<stdbool.h>
#include<stdlib.h>

typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode//每个节点的结构
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

//初始化
void QueueInit(Queue* pq);
//释放
void QueueDestroy(Queue* pq);
//尾插(入队)
void QueuePush(Queue* pq, QDataType x);
//头删(出队)
void QueuePop(Queue* pq);
//队头数据
QDataType QueueFront(Queue* pq);
//队尾数据
QDataType QueueBack(Queue* pq);
//数据个数
int QueueSize(Queue* pq);
//判空
bool QueueEmpty(Queue* pq);


//Queue.c
#include"Queue.h"
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}


void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);

	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail\n");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;

	if (pq->ptail == NULL)
	{
		assert(pq->phead == NULL);

		pq->phead = pq->ptail = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}


	pq->size++;
}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//一个队列
	if (pq->phead->next == NULL)
	{
		free(pq->phead);
		pq->phead = NULL;
		pq->ptail = NULL;
	}
	//多个队列
	else
	{
		QNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	pq->size--;
}

QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}

QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}

int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
	/*return pq->phead == NULL && pq->ptail == NULL;*/
	return pq->size == 0;
}


//Test.c
#include<stdlib.h>
#include<stdio.h>
#include<assert.h>
#include"Queue.h"

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	node5->left = node7;
	return node1;
}


void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

//二叉树节点个数 --- 遍历计数
//int size = 0;
//void BTreeSzie(BTNode* root)
//{
//	if (root == NULL)
//	{
//		return size;
//	}
//	size++;
//	BTreeSzie(root->left);
//	BTreeSzie(root->right);
//	return size;
//}

//int BTreeSzie(BTNode* root)
//{
//	static int size = 0;
//	//printf("%p,%d\n", &size,size);
//	if (root == NULL)
//	{
//		return size;
//	}
//	size++;
//	BTreeSzie(root->left );
//	BTreeSzie(root->right );
//	return size;
//}


int BTreeSzie(BTNode* root)
{
	return root == NULL ? 0 :
		BTreeSzie(root->left)
		+ BTreeSzie(root->right) + 1;
}

//二叉树叶子节点个数
int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BTreeLeafSize(root->left)
		+ BTreeLeafSize(root->right);
}

//二叉树树的高度
int BTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int leftHeight = BTreeHeight(root->left);
	int rightHeight = BTreeHeight(root->right);
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

//二叉树第k层的节点个数
int BTreeLevelKSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BTreeLevelKSize(root->left, k - 1)
		+ BTreeLevelKSize(root->right, k - 1);
}

//二叉树查找值为x的节点
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	/*BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1)
		return ret1;
	BTNode* ret2 = BTreeFind(root->left, x);
	if (ret2)
		return ret2;
	return NULL;*/
	//BTreeFind(root->left, x);
	//BTreeFind(root->right, x);
	//return NULL;
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1)
		return ret1;
	return BTreeFind(root->left, x);
}

//层序遍历---用队列
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	printf("\n");
	QueueDestroy(&q);
}

void BTreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;
	BTreeDestroy(root->left);
	BTreeDestroy(root->right);
	free(root);
}

//判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//遇到空就跳出
		if (front == NULL)
			break;

		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	//检查后面的节点有没有非空
	//有非空不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			return false;
			QueueDestroy(&q);
		}
	}
	return true;
	QueueDestroy(&q);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	PrevOrder(root);
	printf("\n");
	InOrder(root);
	printf("\n");
	PostOrder(root);
	printf("\n");
	//printf("BTreeSize:%d\n", BTreeSzie(root));
	//printf("BTreeSize:%d\n", BTreeSzie(root));
	//printf("BTreeSize:%d\n", BTreeSzie(root));
	/*BTreeSzie(root);
	printf("BTreeSize:%d\n", size);
	size = 0;
	BTreeSzie(root);
	printf("BTreeSize:%d\n", size);
	size = 0;
	BTreeSzie(root);
	printf("BTreeSize:%d\n", size);*/

	printf("BTreeSize:%d\n", BTreeSzie(root));
	printf("BTreeLeafSize: % d\n", BTreeLeafSize(root));
	printf("BTreeHeight: % d\n", BTreeHeight(root));
	printf("BTreeLevelKSize: % d\n", BTreeLevelKSize(root, 3));
	printf("BTreeLevelKSize: % d\n", BTreeLevelKSize(root, 2));
	

	LevelOrder(root);

	printf("BTreeComplete: % d\n", BTreeComplete(root));
	
	BTreeDestroy(root);
	root = NULL;
	return 0;
}

😽总结

请添加图片描述
😽Ending,今天的链式二叉树的内容就到此结束啦~，如果后续想了解更多，就请关注我吧，一键三连哦 ~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/603780.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

​Memcached 架构

​Memcached 架构

Memcached是一种内存中的键值存储&#xff0c;最初是用Perl编写的&#xff0c;后来重写为C语言。它受到Facebook、Netflix和Wikipedia等公司的欢迎&#xff0c;因为它简单易用。 虽然当谈论到软件描述时&#xff0c;“简单”这个词已经失去了意义&#xff0c;但我认为Memcache…
阅读更多...
chatgpt赋能python：用Python制作AI：优化搜索引擎结果的关键

chatgpt赋能python：用Python制作AI：优化搜索引擎结果的关键

用Python制作AI&#xff1a;优化搜索引擎结果的关键 搜索引擎正成为我们日常生活不可或缺的一部分。无论是寻找答案、娱乐还是购物&#xff0c;大多数人都会先打开搜索引擎。随着越来越多的数据被放入互联网中&#xff0c;如何让搜索引擎结果与用户的搜索意图相符&#xff0c;…
阅读更多...
chatgpt赋能python：用Python办公自动化轻松完成繁琐重复的工作

chatgpt赋能python：用Python办公自动化轻松完成繁琐重复的工作

用Python办公自动化轻松完成繁琐重复的工作 随着科技的进步&#xff0c;许多传统工作已经被自动化取代。而在许多职业中&#xff0c;办公自动化通常被认为是节省时间和减少错误的最佳方法。对于那些使用Microsoft Office&#xff0c;例如Excel、Word和PowerPoint等应用程序的用…
阅读更多...
chatgpt赋能python：Python如何删除空白

chatgpt赋能python：Python如何删除空白

Python 如何删除空白 在SEO优化过程中&#xff0c;我们需要保证我们的网页内容的质量和可读性。其中&#xff0c;一个重要的因素是删除空白。在Python中&#xff0c;我们可以使用多种方法来删除空白&#xff0c;下面我们将介绍一些方法并讨论它们的优缺点。 方法一&#xff1…
阅读更多...
操作系统复习4.2.0-磁盘组织和管理

操作系统复习4.2.0-磁盘组织和管理

磁盘的结构 磁盘、磁道、扇区 磁盘划分n圈磁道&#xff0c;每条磁道划分为多个扇区 磁盘读写 磁头移动到需要读写的扇区所在的磁道来完成读写 磁盘转起来让目标扇区在磁头下面划过 盘面和柱面 分类 按磁头分类&#xff1a;磁头可伸缩移动、不可伸缩移动(同一盘面上有多个…
阅读更多...
chatgpt赋能python：Python加入Path的好处及操作方法

chatgpt赋能python：Python加入Path的好处及操作方法

Python加入Path的好处及操作方法 什么是Path&#xff1f; Path&#xff0c;顾名思义就是文件路径的意思。每当我们需要执行某些程序或打开某个文件&#xff0c;电脑都会按照这个文件路径来查找需要的文件或程序。在Windows系统中&#xff0c;文件路径是由一连串的路径名组成的…
阅读更多...
DiffRate详解：高效Vision Transformers的可微压缩率

DiffRate详解：高效Vision Transformers的可微压缩率

DiffRate详解&#xff1a;高效Vision Transformers的可微压缩率 0. 引言1. 相关内容介绍1.1 Transformer Block1.2 令牌修剪和合并1.3 修剪和合并的统一 2 DiffRate中的创新点2.1 令牌排序2.2 压缩率重参数化2.3 训练目标 3. 算法流程4. 总结 0. 引言 就当前的Vision Transfor…
阅读更多...
决策树分类算法

决策树分类算法

#CSDN AI写作助手创作测评 目录 ID3算法 1.算法原理 2.代码实现 3.ID3算法的优缺点分析 C4.5算法 1.原理 2.优缺点 心得感受 决策树表示方法是应用最广泛的逻辑方法之一&#xff0c;它从一组无次序、无规则的事例中推理出决策树表示形式的分类规则。在决策树的内部…
阅读更多...
Vue+springboot医院住院挂号登记收费系统7ui9s

Vue+springboot医院住院挂号登记收费系统7ui9s

医院信息管理系统的开发过程中&#xff0c;采用B / S架构&#xff0c;主要使用java语言进行开发&#xff0c;结合最新流行的springboot框架。使用Mysql数据库和idea开发环境。该医院信息管理系统包括用户、医生和管理员。其主要功能包括用户管理、医生管理、医生信息管理、预约…
阅读更多...
chatgpt赋能python：Python删除非字母的SEO文章

chatgpt赋能python：Python删除非字母的SEO文章

Python删除非字母的SEO文章 Python是一个功能强大的编程语言&#xff0c;广泛应用于各类领域&#xff0c;包括搜索引擎优化&#xff08;SEO&#xff09;。在进行SEO优化时&#xff0c;有时需要从文本中删除非字母字符。这可以用Python快速高效地完成。本文将介绍如何使用Pytho…
阅读更多...
基于PyQt5的图形化界面开发——堆栈动画演示

基于PyQt5的图形化界面开发——堆栈动画演示

目录 0. 前言1. 了解堆栈2.代码实现3. 演示效果其他PyQt5文章 0. 前言 本文使用 PyQt5制作图形化界面演示数据结构中的堆栈操作 操作系统&#xff1a;Windows10 专业版 开发环境&#xff1a;Pycahrm Comunity 2022.3 Python解释器版本&#xff1a;Python3.8 第三方库&…
阅读更多...
图文并茂教你快速入门React系列03-事件

图文并茂教你快速入门React系列03-事件

事件 使用 React 可以在 JSX 中添加 事件处理函数。其中事件处理函数为自定义函数&#xff0c;它将在响应交互&#xff08;如点击、悬停、表单输入框获得焦点等&#xff09;时触发。 事件处理 // 这样写&#xff1a;export default function Button() {function handleClic…
阅读更多...
chatgpt赋能python：Python删除文件的方法与注意事项

chatgpt赋能python：Python删除文件的方法与注意事项

Python删除文件的方法与注意事项 在Python中&#xff0c;删除文件是很常见的操作。通常&#xff0c;我们需要在程序中删除不再需要的文件&#xff0c;或者在清理本地存储空间时删除缓存文件。本文将重点介绍Python如何删除文件以及可能涉及到的注意事项。 如何删除文件 Pyth…
阅读更多...
redis设计原理009持久化策略

redis设计原理009持久化策略

目录 RDB 备份原理 优点 缺点 AOF 不能保证绝对不丢失数据 重写 流程 结论 优点 缺点 如何选择RDB和AOF 同时开启 混合模式 运行过程 数据 数据恢复 优点 缺点 优化方案 总结 RDB 通过快照&#xff08;snapshotting&#xff09;完成的&#xff0c;当符合一定…
阅读更多...
写一个python文件，在shell脚本中运行

写一个python文件，在shell脚本中运行

最近要复现论文了&#xff0c;发现代码的主函数在.py文件中&#xff0c;运行脚本是在.sh中。 要命的事&#xff0c;我不懂&#xff0c;我怎么debug。 1.新建一个pycharm项目&#xff0c;新建main.py import argparsedef get_args():parser argparse.ArgumentParser()parser…
阅读更多...
chatgpt赋能python：Python模块的优势和局限性

chatgpt赋能python：Python模块的优势和局限性

Python模块的优势和局限性 引言 Python作为一门高级编程语言&#xff0c;被广泛应用于各种领域。其中&#xff0c;Python内置的模块系统&#xff0c;为Python在编程中的灵活性和可扩展性提供了很大的优势。在本文中&#xff0c;我们将探讨Python模块的优势和局限性及其对Web优…
阅读更多...
chatgpt赋能python：用Python剔除重复内容提升SEO效果

chatgpt赋能python：用Python剔除重复内容提升SEO效果

用Python剔除重复内容提升SEO效果 SEO是指通过优化网站结构和内容&#xff0c;在搜索引擎中获得更高的排名&#xff0c;从而提升网站流量和曝光度的一种网络营销方式。网站内容是SEO工作的重要组成部分&#xff0c;而剔除重复的内容对于SEO效果的提升有着重要的作用。本文将介…
阅读更多...
chatgpt赋能python：Python制作人机交互界面：完美融合技术和用户体验

chatgpt赋能python：Python制作人机交互界面：完美融合技术和用户体验

Python 制作人机交互界面&#xff1a;完美融合技术和用户体验 随着人工智能和互联网技术的发展&#xff0c;人机交互一直是非常热门的话题。Python 作为一门功能强大&#xff0c;应用广泛的高级编程语言&#xff0c;同样在这个领域发挥了重要作用。Python 制作人机交互界面&am…
阅读更多...
【列表迭代器和增强for循环】

【列表迭代器和增强for循环】

列表迭代器和增强for循环 1.列表迭代器 ListIterator&#xff1a;列表迭代器 通过List集合的listIterator()方法得到&#xff0c;所以说它是List集合特有的迭代器用于允许程序员沿任一方向遍历列表的列表迭代器&#xff0c;在迭代期间修改列表&#xff0c;并获取列表中迭代器…
阅读更多...
SAP ABAP smartforms 创建并实现调用源码（下）

SAP ABAP smartforms 创建并实现调用源码（下）

SAP ABAP smartforms 创建并实现调用源码&#xff08;上&#xff09; smartforms 入门详见上一篇博文。 一&#xff1a;报表程序调用 smartforms 示例&#xff1a;报表选中一行&#xff0c;将这行机相关数据通过表单打印出来。实际例子:采购订单表&#xff0c;销售订单。 调…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023