视频链接：B站-人体关键点检测与MMPose

1. 人体姿态估计的介绍和应用

关键点提取，属于模式识别

人体姿态估计的下游任务：行为识别（比如：拥抱。。）

下游任务：CG和动画，这个是最常见的应用

下游任务：人机交互（手势识别，依据收拾做出不同的响应，比如：HoloLens会对五指手势（3D）做出不同的反应）

2-1. 2D姿态估计概述

包括：

1. 自顶向下方法
2. 自底向上方法
3. 单阶段方法
4. 基于Transformer的方法

2.1 任务描述

2D人体姿态估计的任务：

• 输入：一张包含人体的图像
• 输出：人体关键点（主要关节）的坐标（2D的）

注意，这里的输出是固定对应（预定义的）18个关节的坐标，就是要找这18个位置的坐标

2.2 基于回归

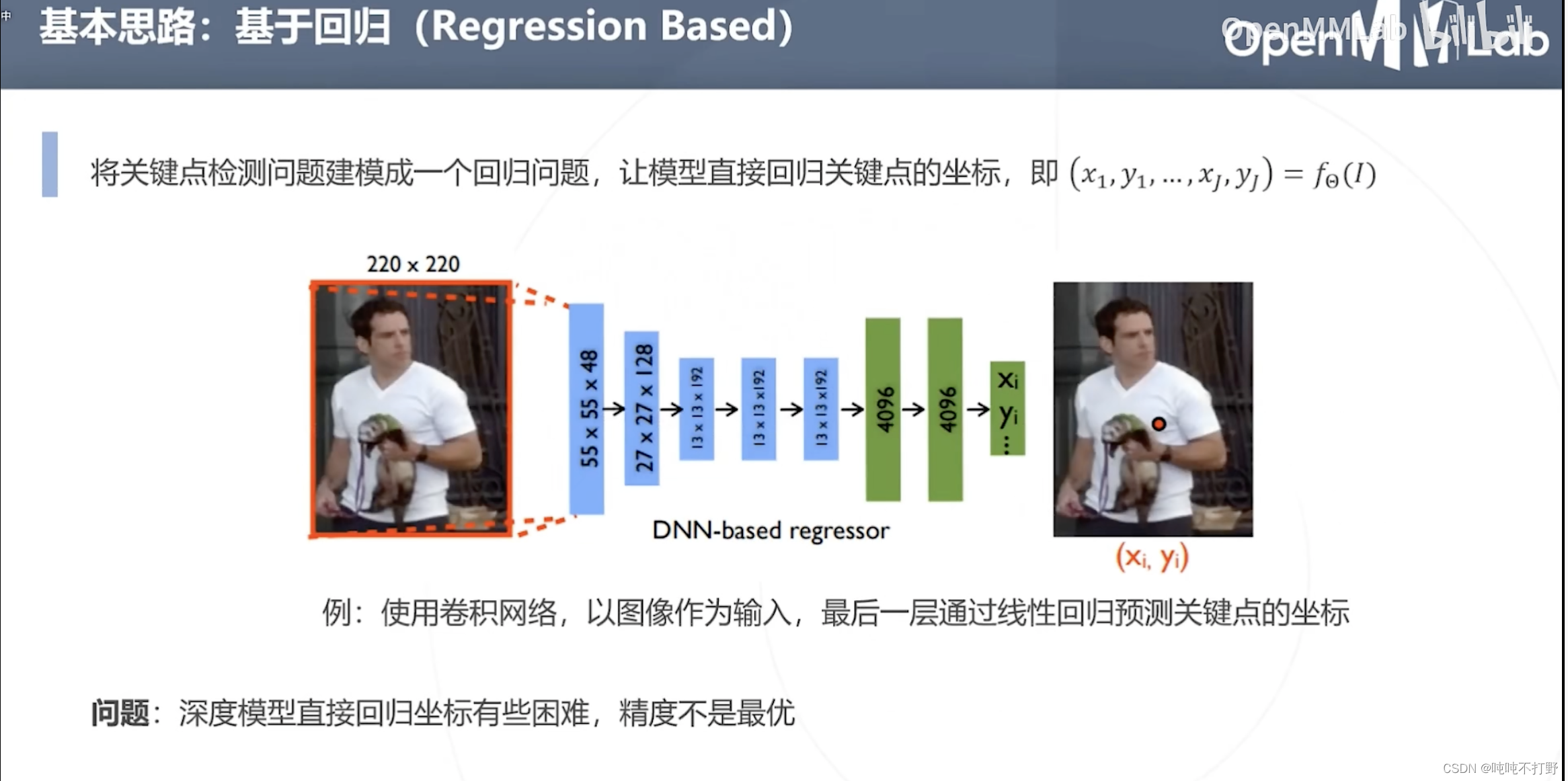
使用深度学习的模型直接回归坐标有些困难，精度不是最优（效果不好）

2.3 基于热力图

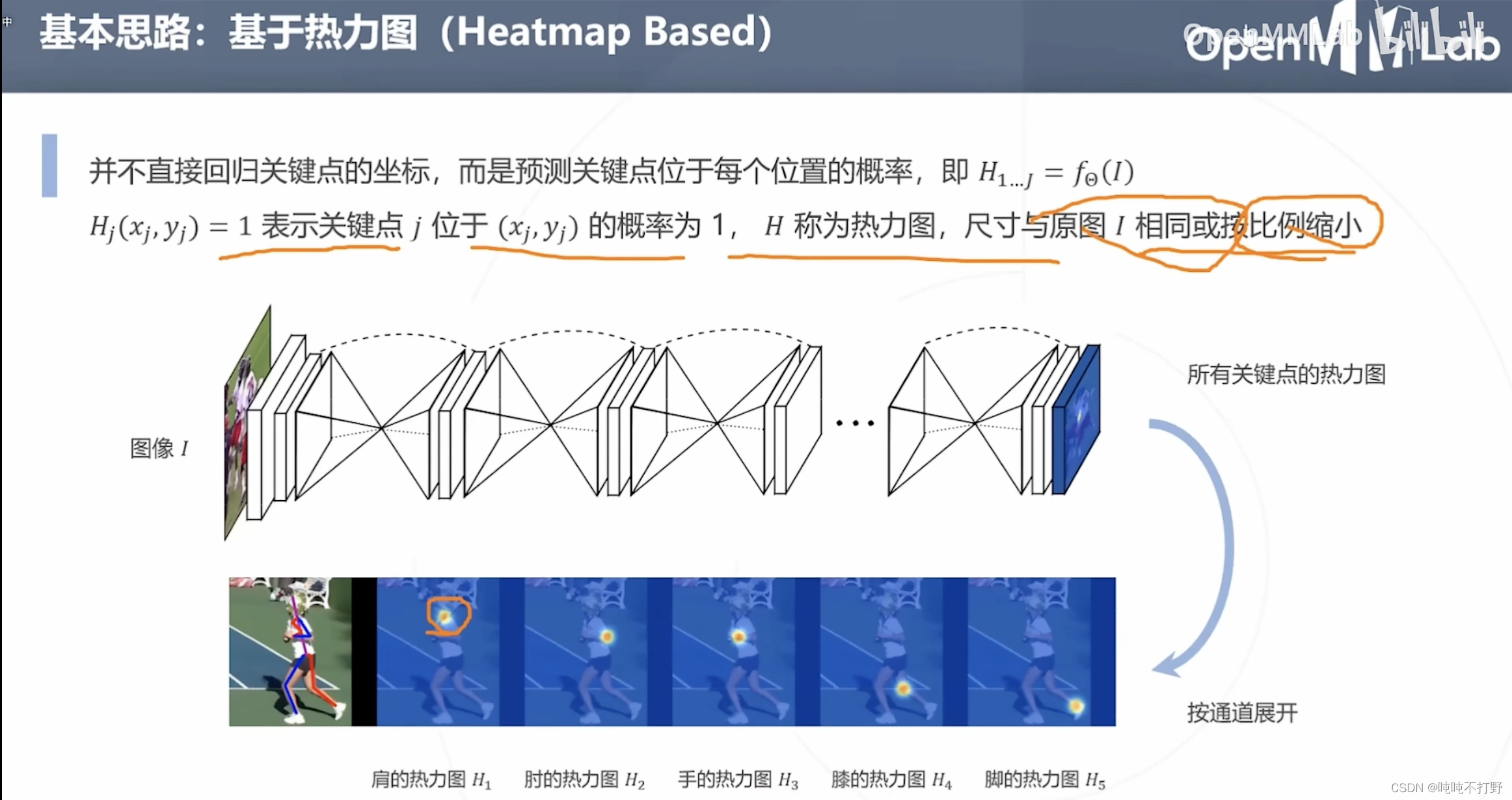
另一种思路是：不直接回归关键点的坐标，而是预测关键点位于每个位置的概率。

• 比如肩的热力图（越靠近肩膀的预定义的关键点，概率越高，颜色逐渐从黄色变成红色）
• 18个关键点，对应18个热力图

基于热力图天然符合神经网络的卷积算子（对每个像素都进行计算，得到每个像素的概率）

2.3.1 从数据标注生成热力图（高斯函数）

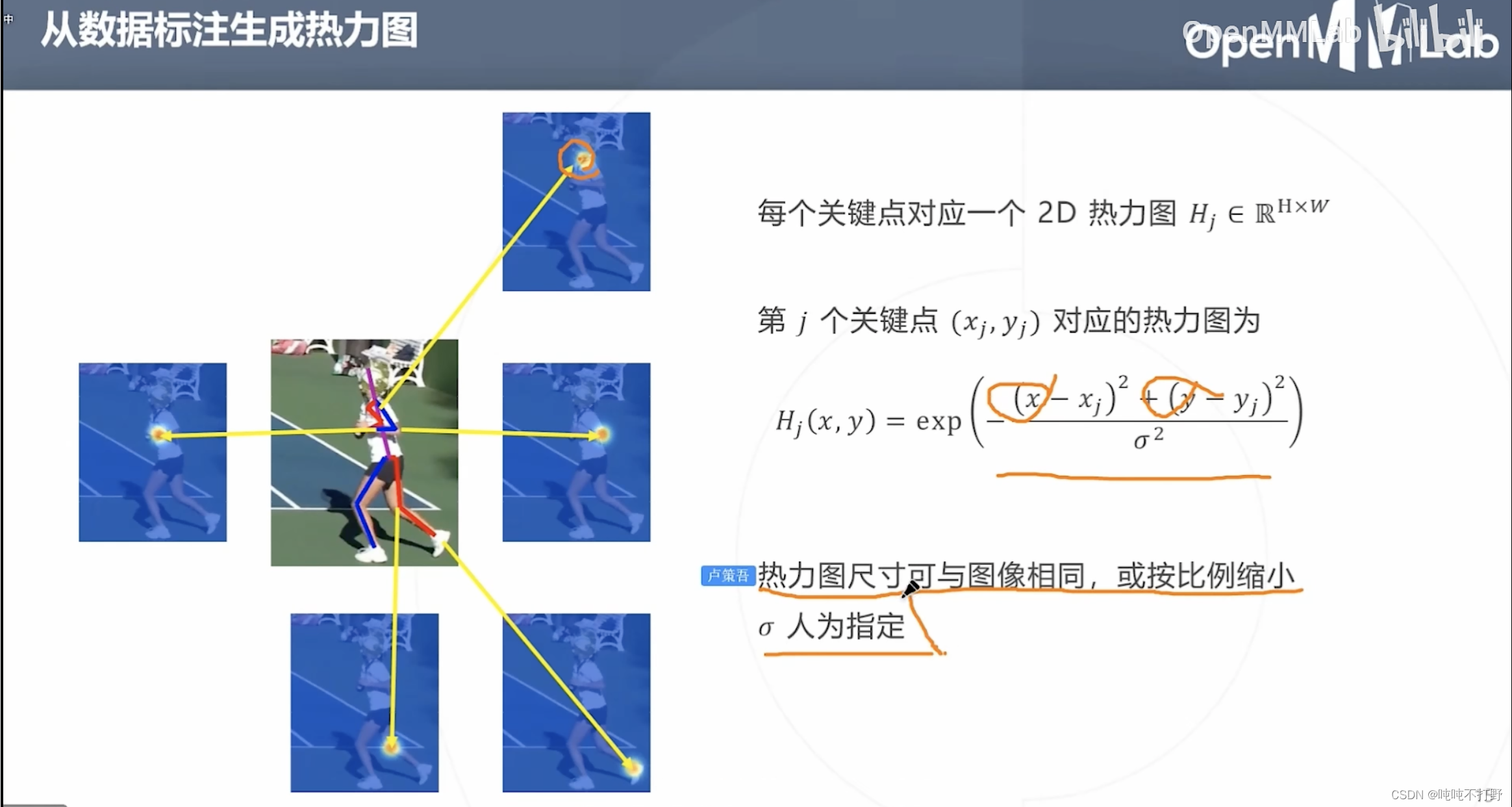
如果想要使用基于热力图的方式，那么首先要根据已有的标注数据生成热力图。

• 预定义的关键点附近区域的概率其实符合这一事实：
  • 越靠近预定义的关键点，概率越高，如上图，颜色逐渐从黄色变成红色
  • 假设上面这个热力图区域是个圆形，那么任意一个直径作为$x$轴(距离预定义关键点的距离作为自变量)，是关键点的概率作为$y$轴（因变量），则可以用高斯函数来描述$x$和$y$的关系
• 所以这里是假设关键点区域的热力图符合高斯分布，来生成热力图（概率图），来进行训练。
• 所以这里说热力图的尺寸，即作为控制高斯函数图像钟的宽度的$\sigma$参数，也就是控制热力图区域大小

---

复习一下高斯函数（红色线代表标准正态分布）：


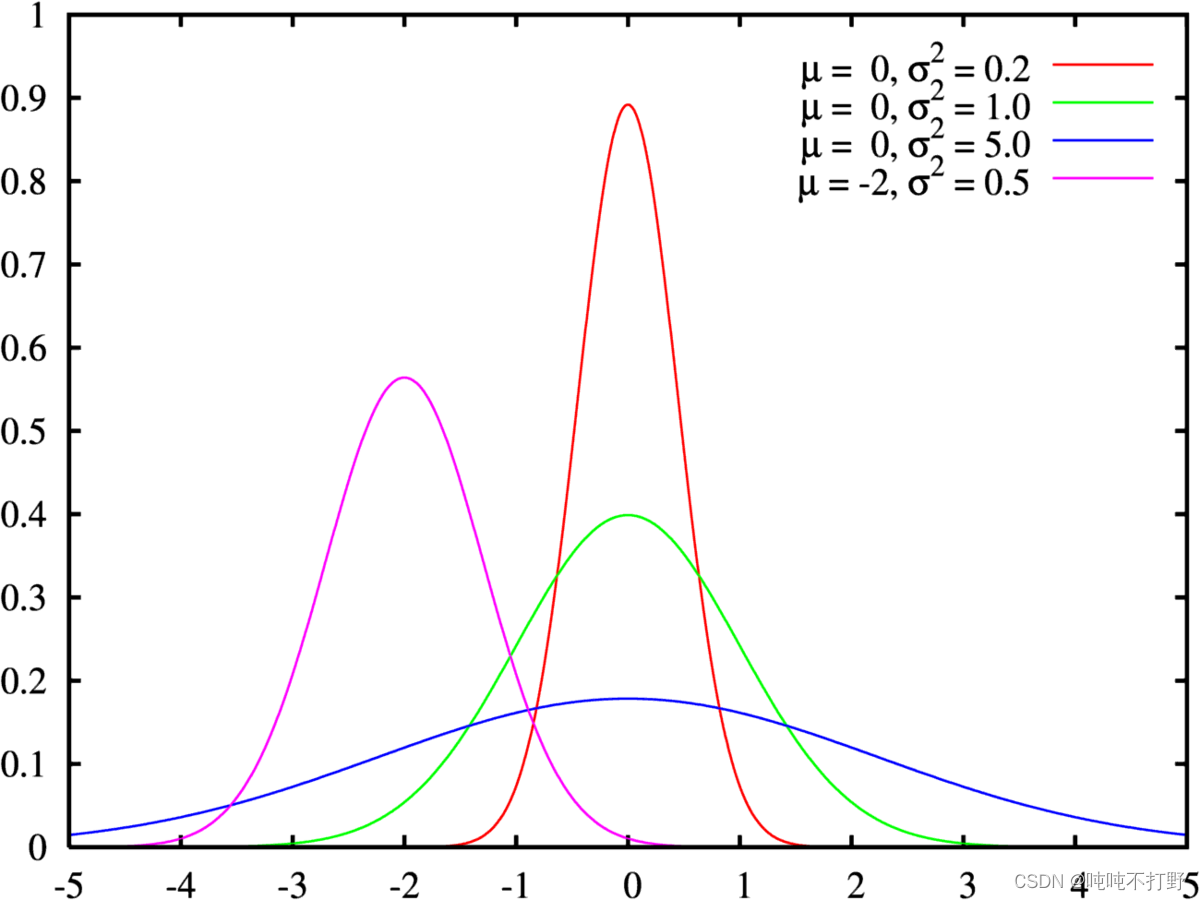
上图是用期望值及方差作为参数表示的高斯曲线

---

高斯函数是正态分布的密度函数，下图的红色是标准正态分布

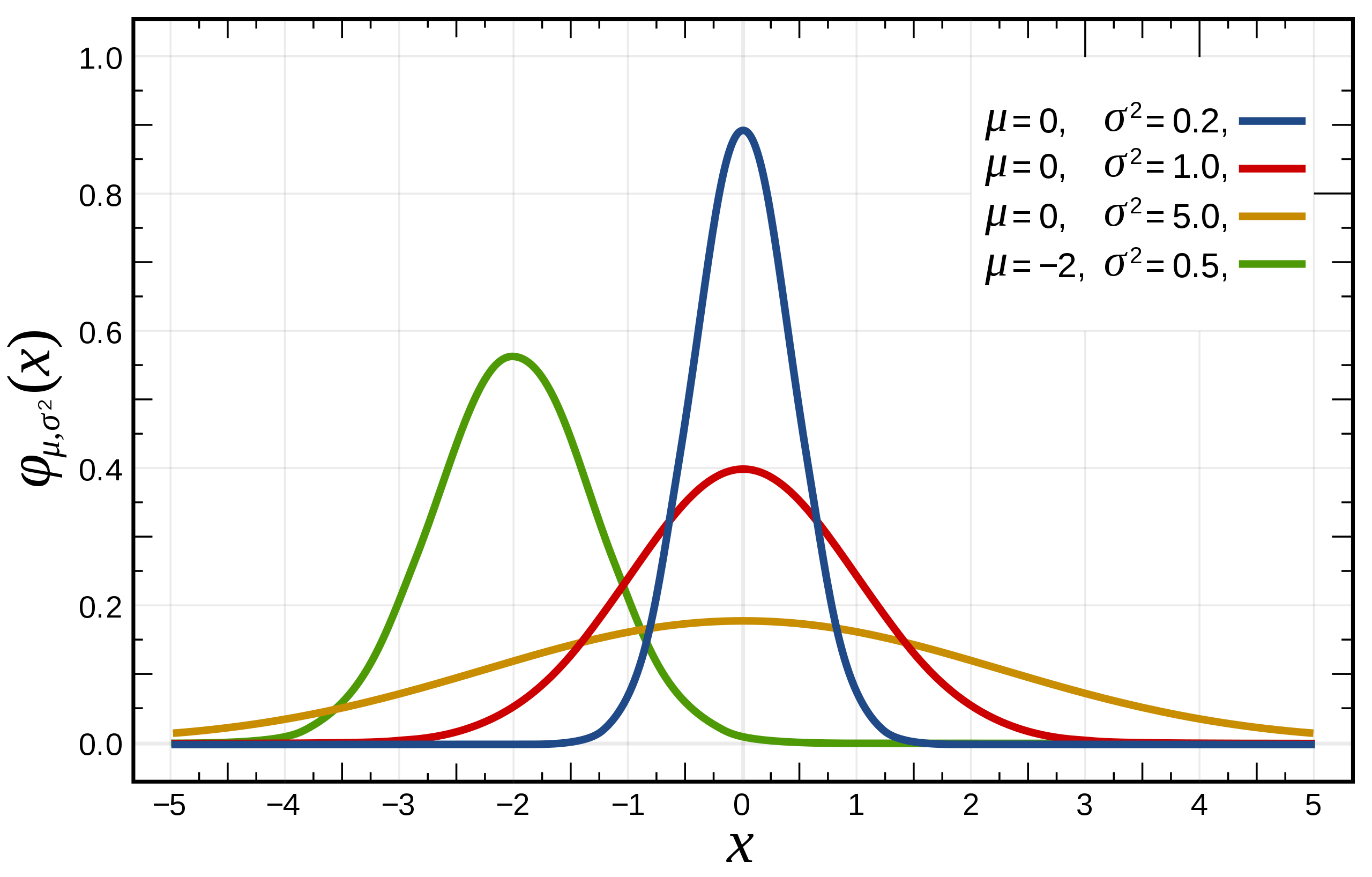
正态分布的数学期望值或期望值$\mu$等于位置参数，决定了分布的位置；其方差${\sigma }^2$的开平方或标准差$\sigma$ 等于尺度参数，决定了分布的幅度。

可以直接看：

• 中文wiki百科-高斯函数
• 中文wiki百科-正态分布
• 打不开上面这个看下面转载的这个，旧了点，但是意思差不多：高斯分布（Gaussian distribution）/正态分布（Normal distribution）

---

2.3.2 使用热力图训练模型

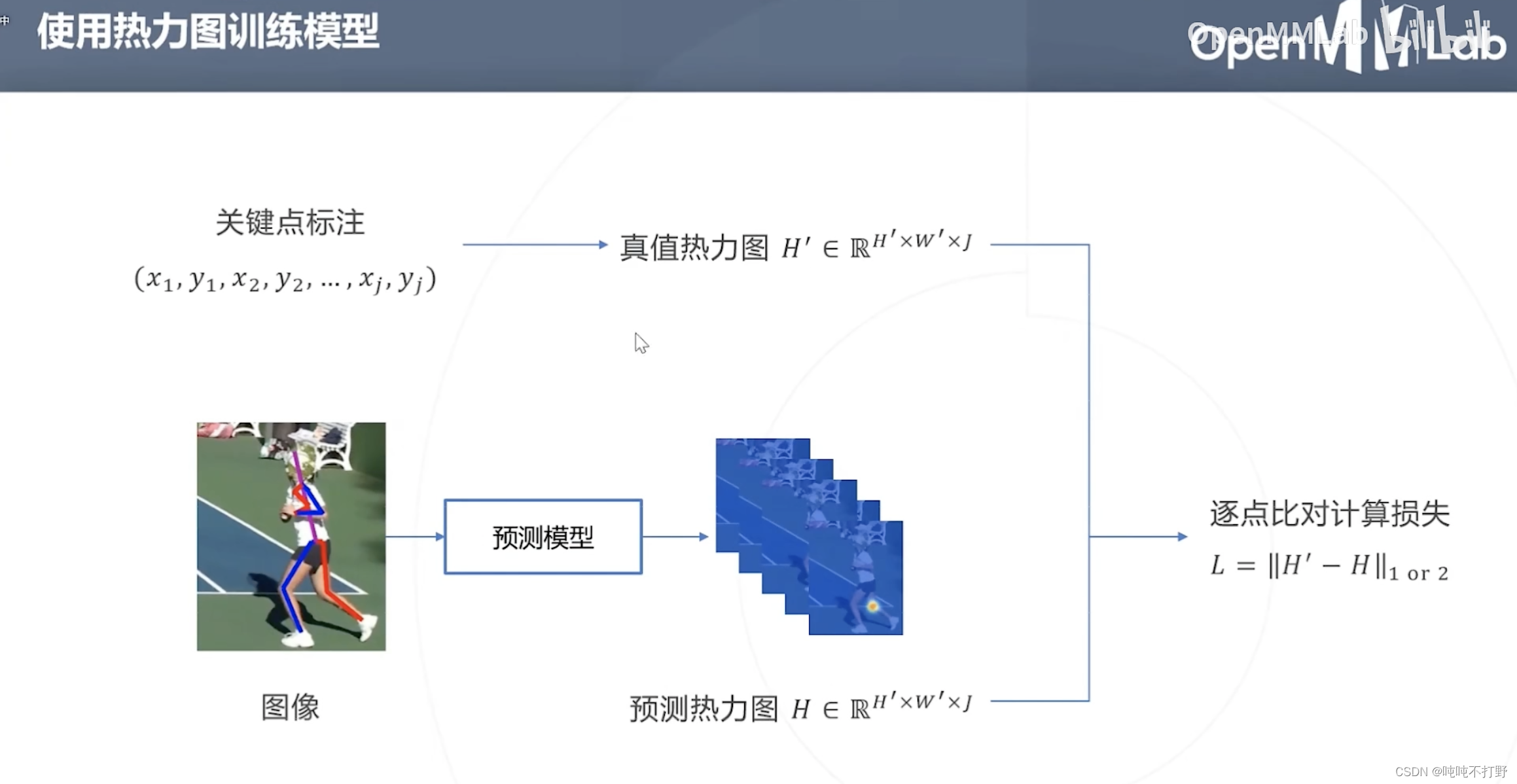
将通过关键点标注生成的真值热力图，作为True label，与预测模型预测出来的热力图Predict label逐点比对（就是关键点附近那一小片区域的热力图），计算损失

所以基于热力图的方法关键就是中心点位置$(x_j,y_j)$（训练目标，优化的参数）和区域大小$\alpha$（可以是超参，也可以基于图像缩放得到，缩放系数也是超参）

• 这里其实是一个2D的高斯函数，$(x_j,y_j)$其实就对应上面高斯函数图像的最高点
• 即，真值热力图的构建函数需要满足：距离关键点越近，概率越大，所以高斯函数天然满足这个性质
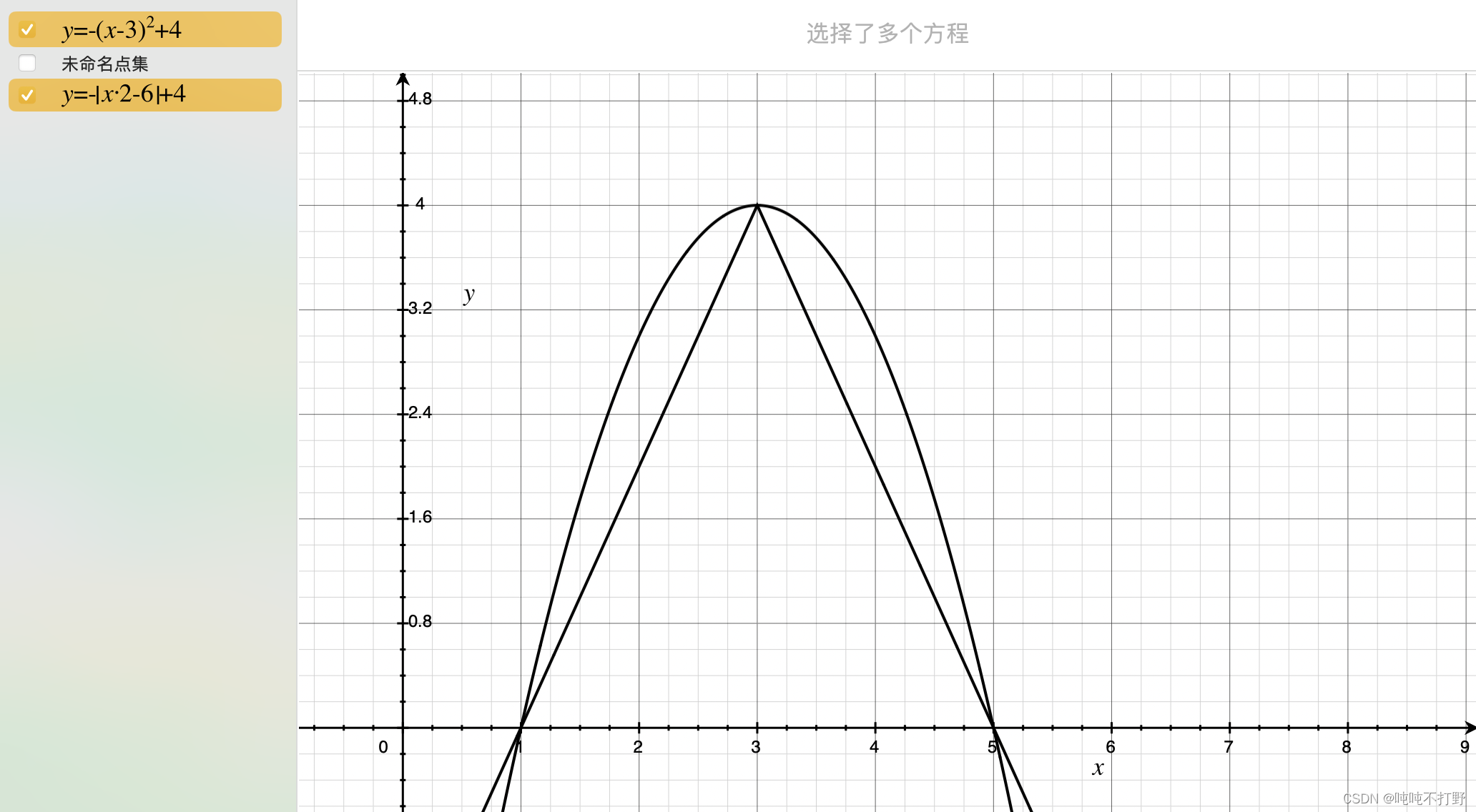
• 除此之外，其实只要是类似钟形都可以，下面这个抛物线函数，还有我随便造的一个绝对值函数，其实都满足这个条件（但是概率取值范围[0,1]需要进一步处理一下才行）
  

---

2.3.3 从热力图还原关键点

• 最直接的办法就是求最大概率（热力图最大值）对应的位置的坐标，
  • 按照生成真值热力图的方式来倒推，是很合理的方式
  • 但这是基于：预测的热力图符合高斯函数，这一假设下的推论
  • 实际上，可能预测的热力图形状不会那么规整，可能会有多个最大值，所以直接求1个最大值这种方式不够鲁棒

另一种从热力图还原关键点的方式就是：

• 先对热力图的概率进行归一化（对概率用softmax，输出的还是概率），用归一化后的概率计算位置的期望
• 期望就是平均值，在1D的高斯函数图像中，高斯函数的最高点，对应的$x$值，确实是$x$取值范围的均值。
• 可能不一定能取到最高点，但是能取到"重心"，这样利用了整个热力图的概率，相对于上面只看热力图的最大概率，就会比较鲁棒，

这种计算方式还有很好的一个性质：

• 可以进行端到端的训练，还原关键点的方式的公式，是可以求导的，所以能和整个训练过程串起来。
• 比如，一开始训练的时候，网络初始化时，使用的是随机数作为关键点来生成初始预测热力图，第一轮训练完成后，得到生成的热力图，就可以得到一个矫正过的关键点，以此来作为第二轮使用的热力图的初始值，继续迭代。
• ❓❓❓但是上面优化的时候只使用热力图的loss， 但是真实关键点和预测关键点也都可以拿到，关键点的loss其实也可以加上去。两种损失一起会更好吗？？

2.4 自顶向下

上面讲的是单人的姿态估计，但是也会有多人姿态估计

最直观的一种方式（自顶向下）：

1. 先目标检测，得到每个人（检测器的精度需要保证）
2. 再对每个人进行 单人姿态估计

模型串联的坏处，

• 姿态估计结果会过分依赖人体目标检测的结果
• 速度和计算量和画面中的人数成正比

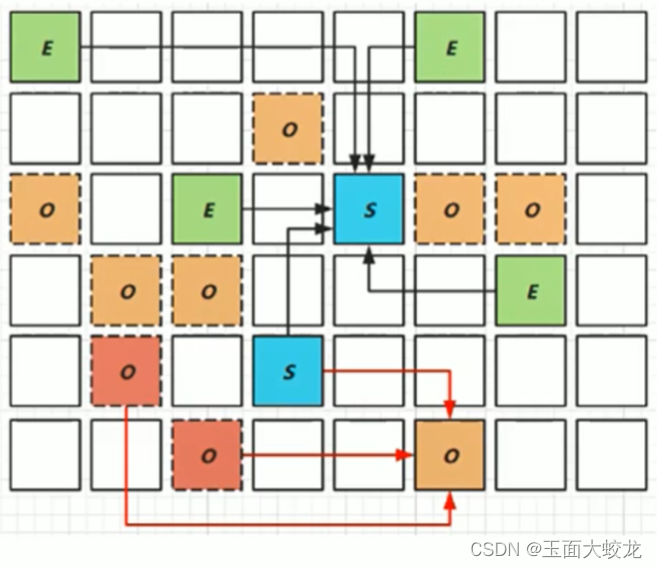
2.5 自底向上

自底向上方法：先把关键点检测完，再去聚类其属于哪个人

优点：

• 推理速度和画面中的人数无关
• 关键点多，则检测速度肯定也会慢一些。但不会像自顶向下方法一样与人数成正比，人数越多的时候，自底向上比自顶向下方法快的越明显）
• 聚类耗时肯定是和人数成正比的

2.6 单阶段方法

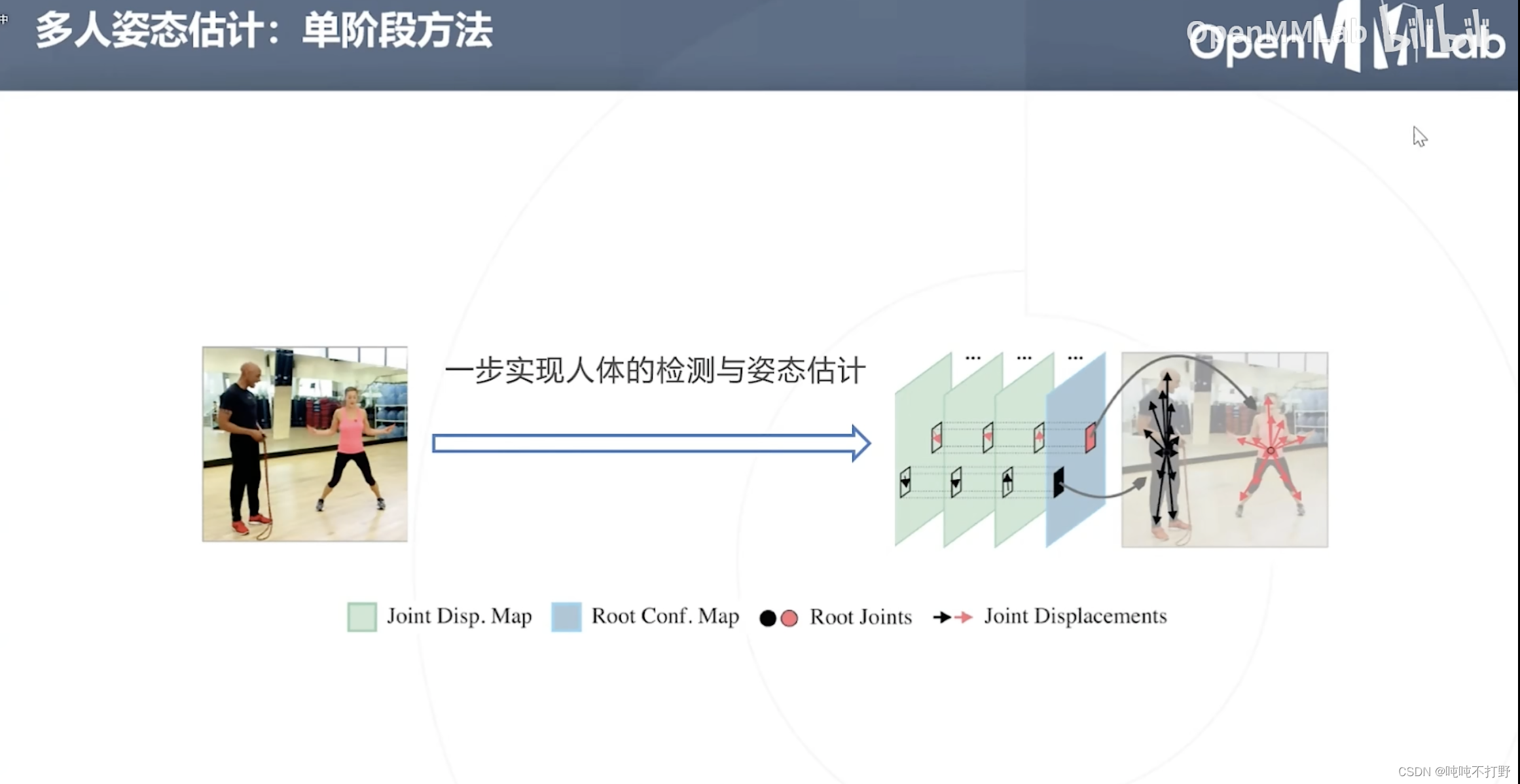
2-2. 2D姿态估计详细说明

2.1 基于回归的自顶向下方法

2.1.1 经典方法

以分类网络为基础，将最后一层分类改为回归，一次性预测所有J个关键点的坐标

• 如果是人体姿态估计的话，就是18个关键点的坐标，在2D场景下，也就是要预测36个数字。。。（回归36个数字，可比分类36个类要难，目标检测里也有回归box四个坐标的方法）
• 原始论文是用AlexNet主干+回归头做的，主干（backbone）也可以换成ResNet等结构

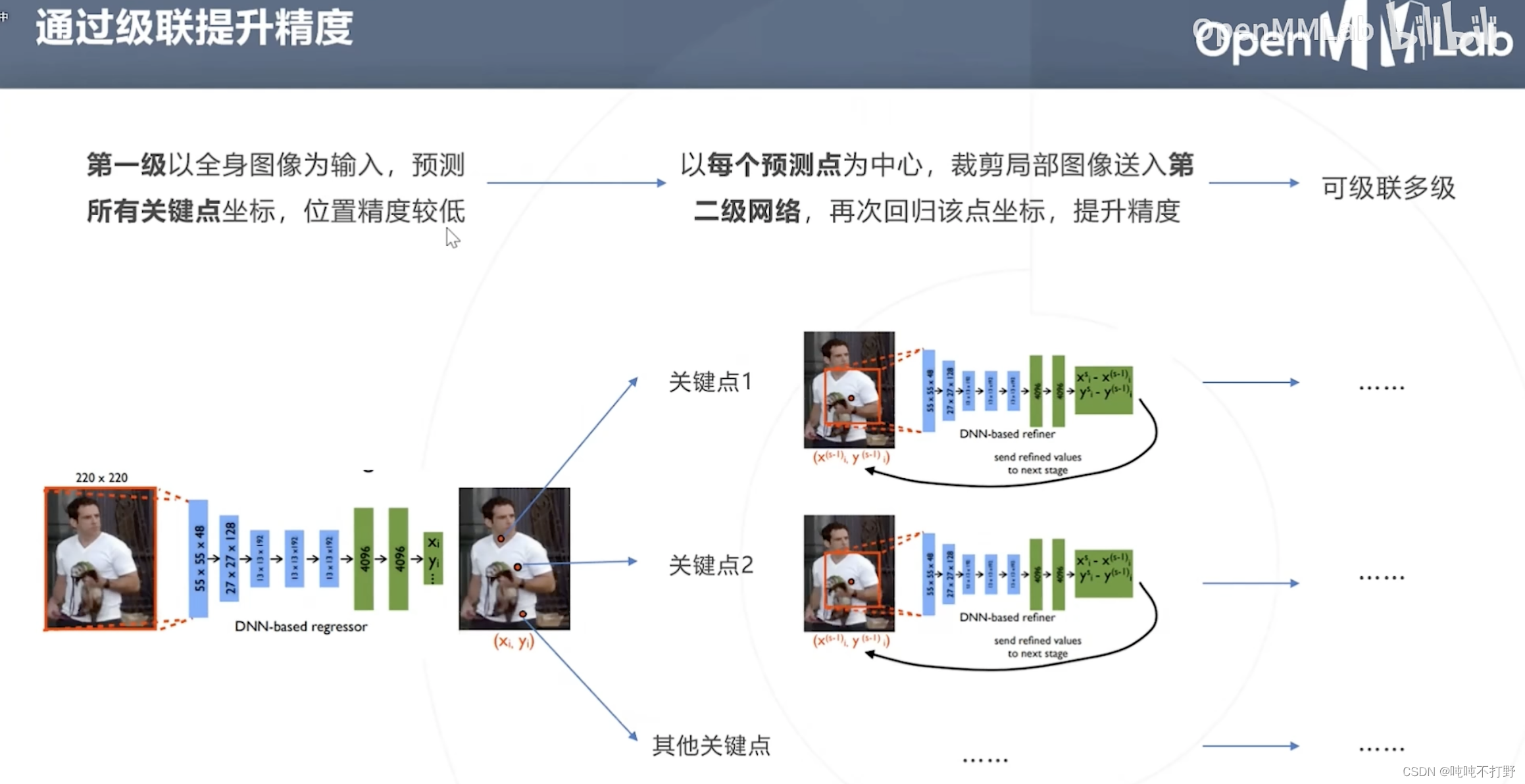
网络结构不变的情况下，使用级联模型的方式，来提高精度。

• 第一级，输入：全身图像
• 第二级，输入：第一步预测点为中心的裁剪后的局部区域

类似医疗影像分割里的级联：

• 第一级，输入：医疗影像
• 第二级，输入：医疗影像+第一级得到的概率图

优势：

1. 回归模型理论上可以达到无限精度，热力图方法的精度受限于特征图的空间分辨率（也不一定，加个期望上去有时候也可以突破这个限制）
2. 回归模型不需要维持高分辨率特征图，计算更高效。相比之下，热力图方法的特征图的size不能低于热力图的size，所以热力图方法确实要计算和存储高分辨率特征图，计算成本（硬件要求）更高

劣势：

• 图像到关键点坐标的映射是高度非线性的，导致直接回归坐标，比通过热力图（概率）得到坐标更难，同时回归方法的精度也低于热力图，因此DeepPose提出之后很长一段时间，2D关键点预测算法主要都是基于热力图的。

2.1.2 基于最大似然估计的改进（RLE）

之前的基于回归方法的姿态估计，

• 损失函数为：真实关键点位置${\mu }_g$与模型预测关键点位置$\tilde{\mu }$的误差作为损失
  • 这背后隐含了高斯分布的假设，即：预测点距离关键点越近，就越好，因此以关键点为圆心，相同半径圆周上的点作为预测点，其误差都是一样的。即:认为预测点分布在真实点形成的一个圆形里。
  • 但是实际上，人体的关节有不同的形状如下图：踝关节，红色是关键点，蓝色围成的区域就是分布，不是个圆形，不是只靠一个方向的距离就可以衡量误差的（每个方向距离引起的误差在损失函数中权重应该是不同的）：
    

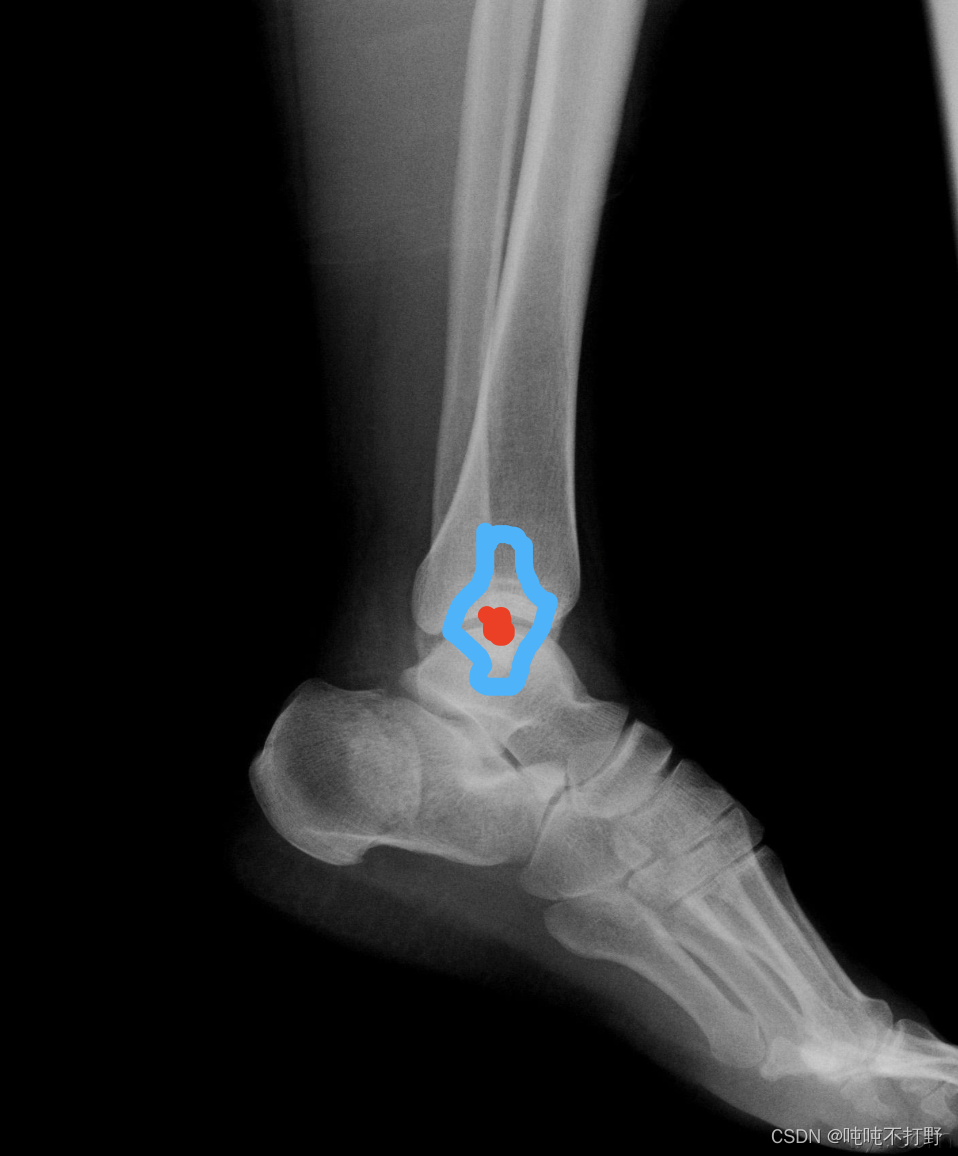
另外，下面这篇文章创新点的部分，要先去看下面的背景知识，看完就基本就懂这个创新点了。

• 模型给出基础分布的参数
• RLE模块基于标准化流，给出位置的分布

论文就直接在MMPose里找了，这里Topdown Regression + Mobilenetv2 + Rle on Coco

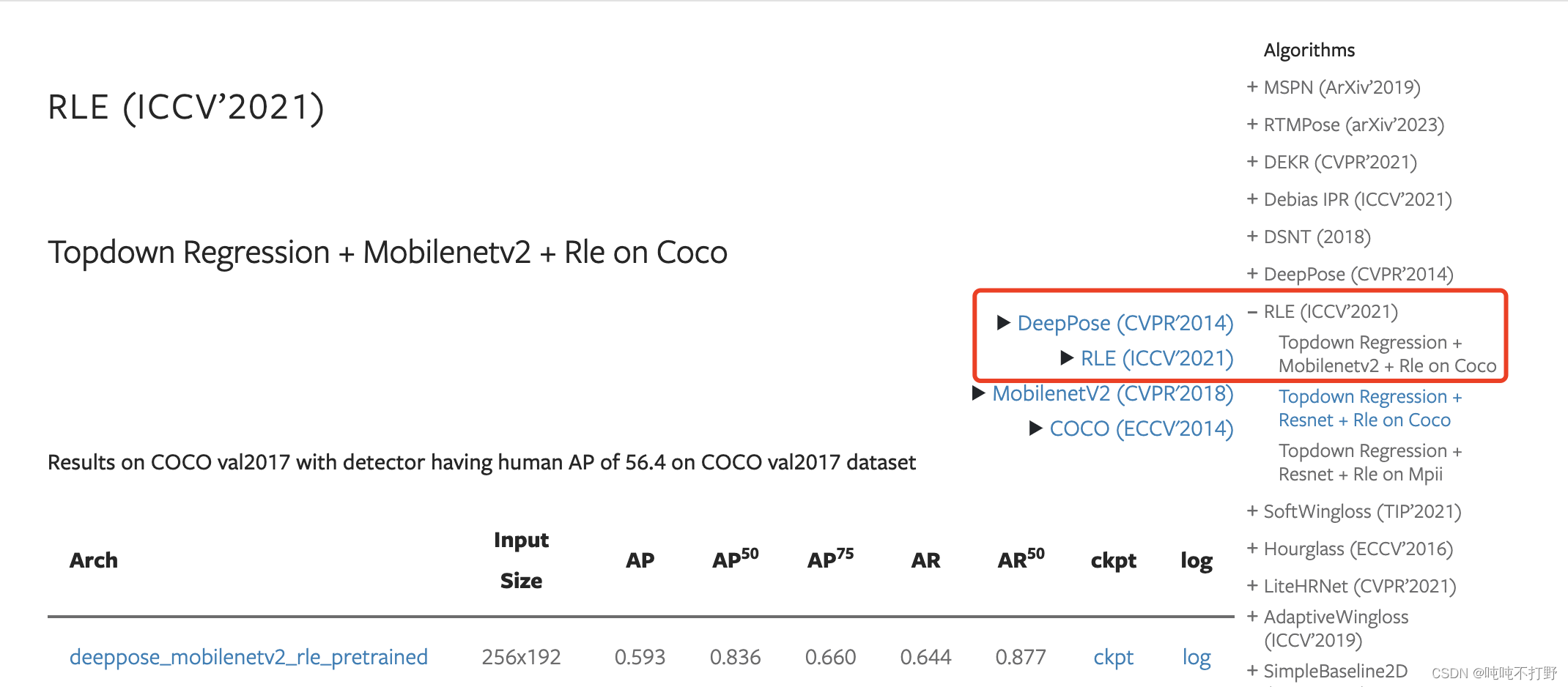
论文arxiv链接：Human Pose Regression with Residual Log-likelihood Estimation

---

2.1.2 背景知识-回归和最大似然估计的联系

• 关于二范数(L2-norm损失函数)这个名词，可以看看：区分混淆概念之L2范数，L2范数损失，L2损失，均方误差
• 如上面的右图，使用二范数（最小二乘误差/最小平方误差）进行回归
  • 其实隐含了 关键点位置 符合 固定方差的各向同性的高斯分布 的假设，但是实际上，在真实的人体关节，关键点的位置并不一定符合高斯分布
• 因此RLE的关键在于：
  • 将简单的高斯分布替换为一个可学习的、表达能力更强的分布（用在损失函数上），来更好指导模型学习真实的关键点位置分布。
  • 因为基于高斯分布假设的回归误差，和高斯似然下的最大似然估计是等价的
• 注意，这里的二范数误差回归的各向同性高斯分布，是基于回归的方法用在损失函数上的；但是原理和基于热力图的方法里，使用标注关键点生成热力图的思想是类似的。

2.1.2 背景知识-标准化流Normalizing Flow

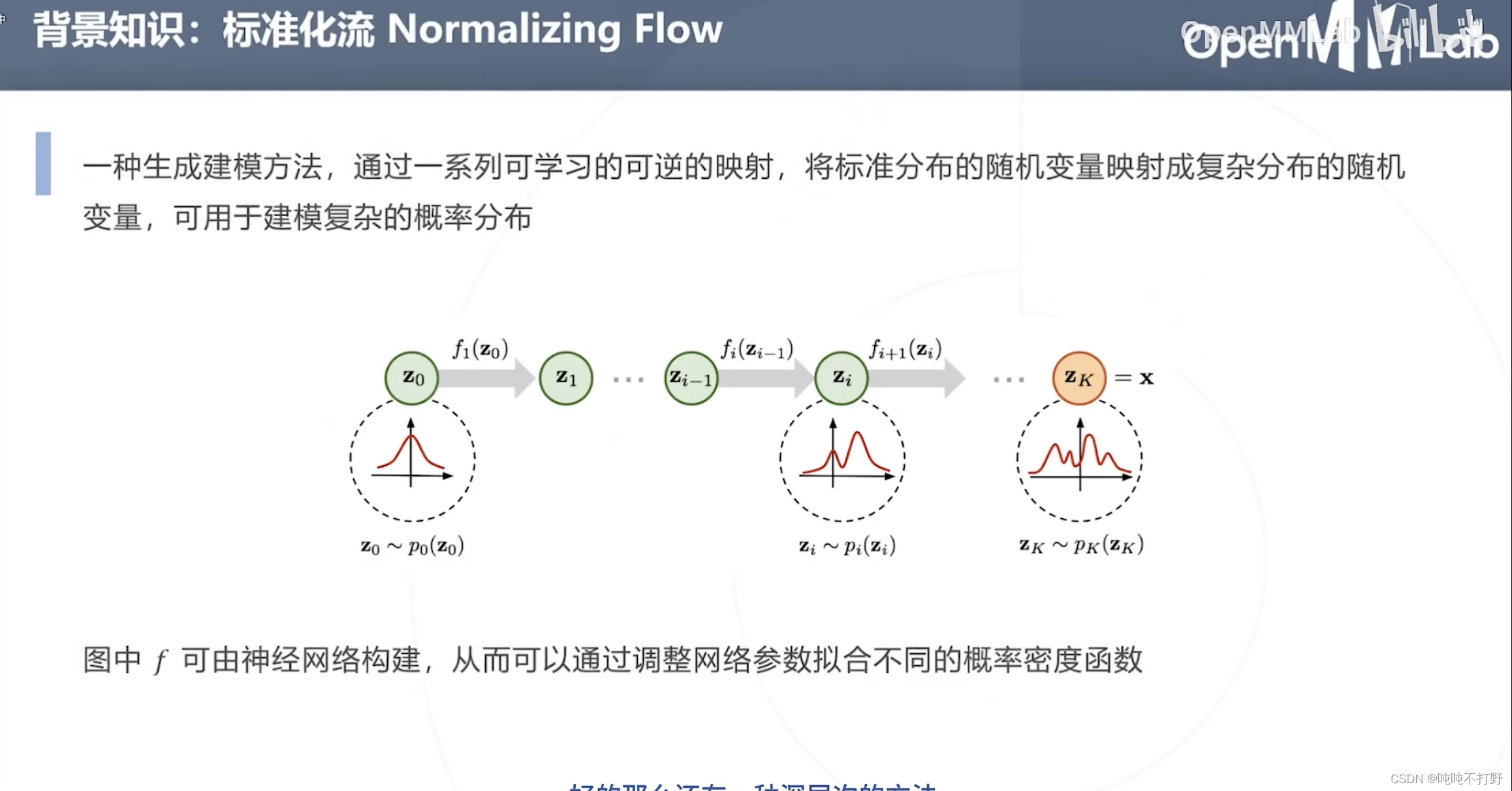
标准化流Normalizing Flow：

• 一种生成建模方法，通过一系列可学习的可逆的映射($f$是学习出来的，同时要满足是可逆的)，将标准分布的随机变量映射成复杂分布的随机变量，可用于建模复杂的概率分布
• $p_0$是标准分布，解析式已知，可以计算其导数等性质
• 后面所有对$z_0$进行的变换$f$，都是由神经网络构建的（学习得到所有的映射$f$）

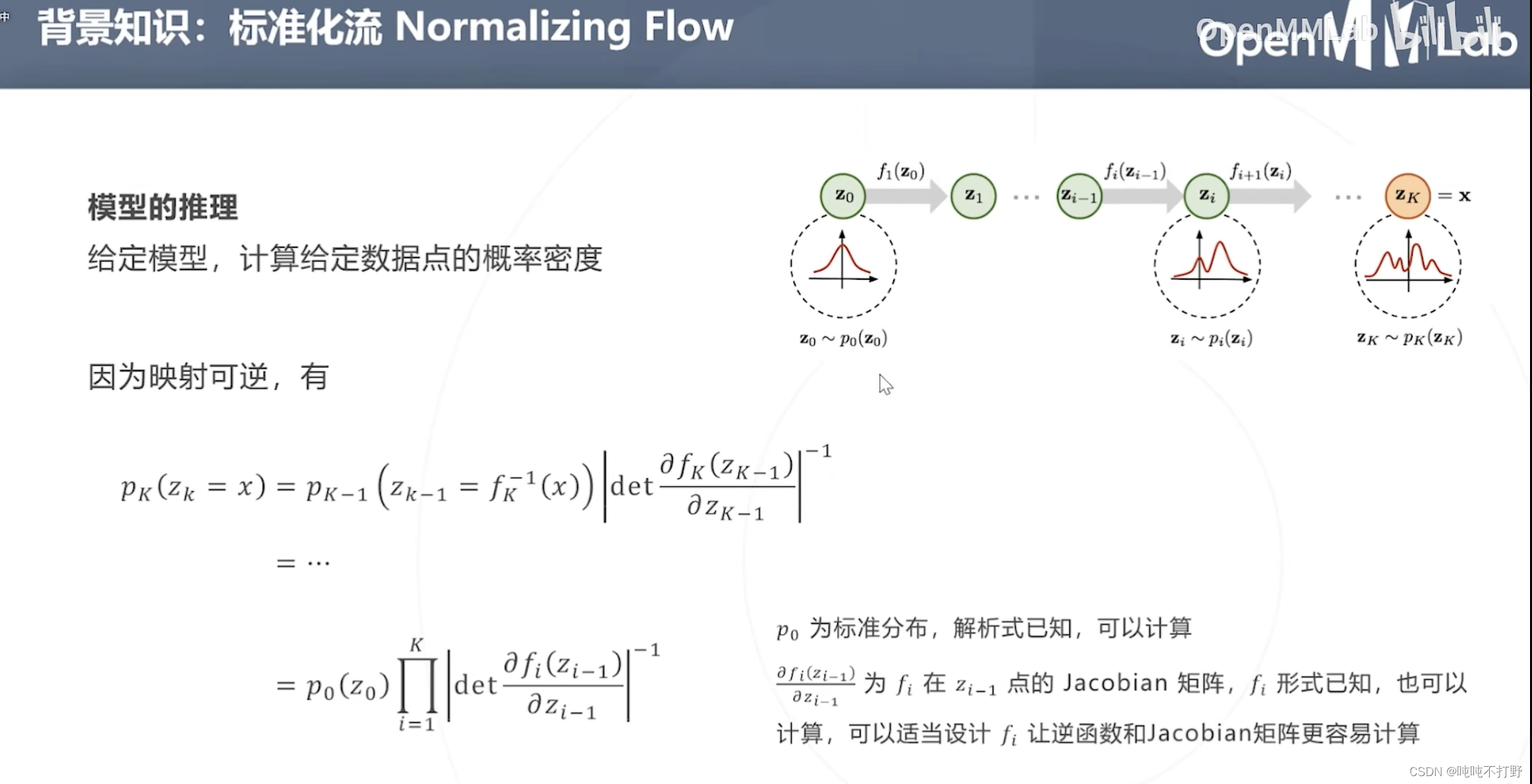
在学习确定所有$f$的准确形式后，考虑根据$f$反向推导出$p_0(z_0)$（模型推理），在模型参数确定($f$已知）后，计算给定数据点(例如：$x$）的概率密度（$p_K(z_K=x)$）

• 由于$f$可逆，所以可以进行上述的推导（概率论知识）
• det：是行列式（Determinant）的缩写，表示计算一个矩阵的行列式,不记得的可以看看：
  • CSDN博客：矩阵 行列式的计算
  • 百度百科-det
  • 知乎文章-矩阵求导（工具书)->4. 行列式的运算

模型学习（求解损失函数，对损失函数进行化简）上述公式，对$p_k(x)$取对数，

• 这样乘法${\prod }_{i=1}^k$就变成了加法${\sum }_{i=1}^k$（这个latex语法是’\prod’，product是乘积的意思）,
• 注意，后面的det外面还套了个-1，因此就变成$p_0(z_0)-{\sum }_{i=1}^{K}log|det\frac{\partial f_i(z_{i-1})}{\partial (z_{i-1})}|$了
• 全体参数$\Phi$，latex-\Phi

概率分布$p_K$受到构建该分布的神经网络$f_1,...,f_K$的全体参数$\Phi$控制

• 可以通过梯度下降优化$\Phi$，这里会涉及对Jacobian的行列式的梯度的计算，可以通过适当映射$f_i$映射的函数形式，让这个计算变简单。
• RLE论文使用的标准化流模型是RealNVP

–

2.1.2 RLE的整体设计

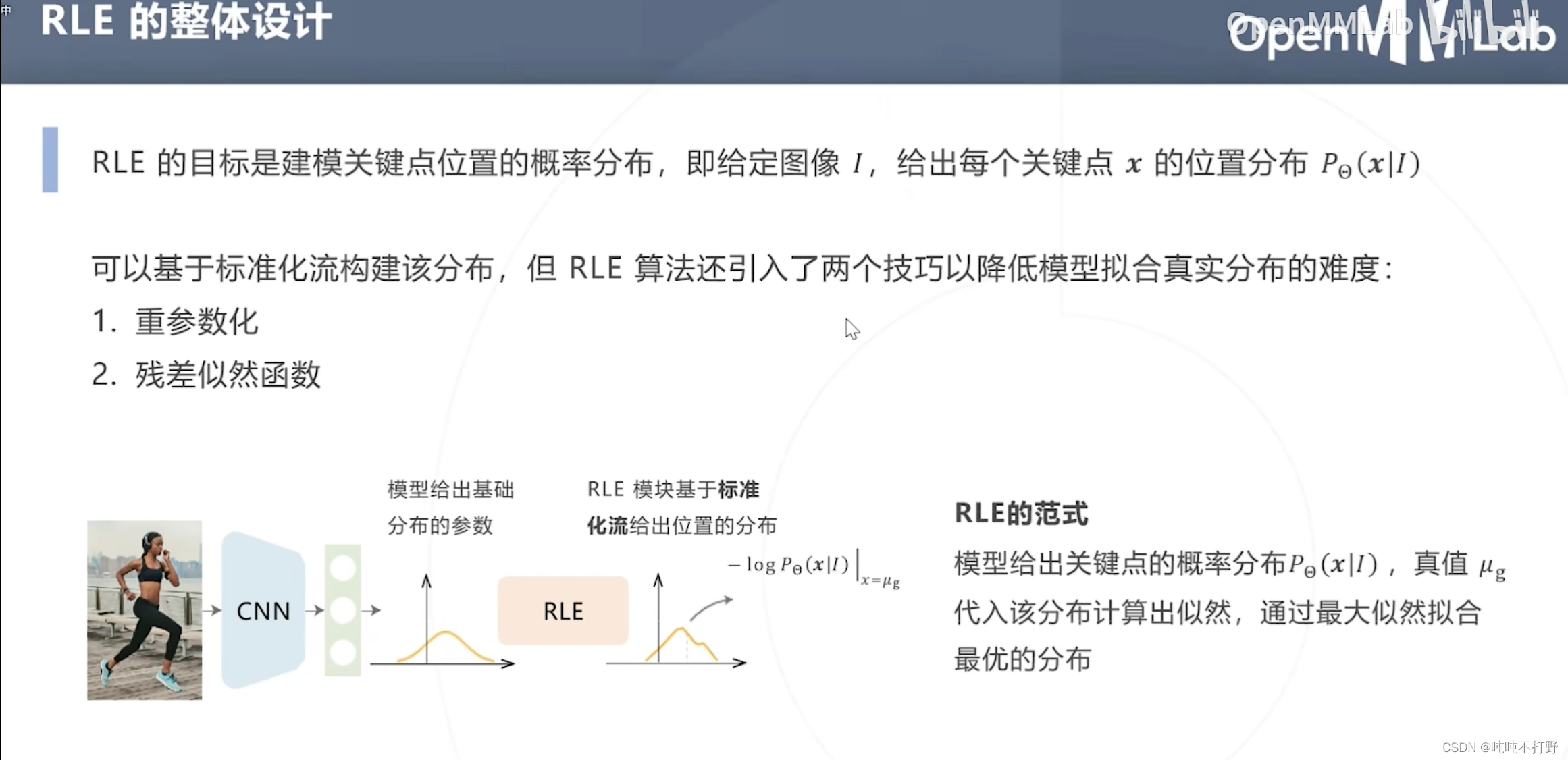
除了基于标准化流构建分布（RLE的主要目标，找出关键点的位置分布），RLE还使用了以下两个技巧来降低模型拟合真实分布的难度：

1. 重（chong）参数化
2. 残差似然函数

为降低建模分布的难度，假设所有关键点的分布属于同一个位置尺度族，即所有分布由某个零均值的基础分布通过平移缩放得来。（重参数化，重复一部分参数）

• 例如：所有一元正态分布$\mathcal{N}(x|\mu ,\sigma )$构成位置尺度族，基础分布为标准正态分布。
  对标准正态分布进行平移缩放，就可以得到任意其他的一元正态分布。
• 重参数化的思想，有点像，卷积层的参数共享（卷积核/模板参数共享），都是为了减少参数，所以公用了一部分参数

所以整体就是：

• 标准化流拟合基础分布$\bar{x}$
• 卷积网络预测平移缩放参数$\tilde{\mu },\tilde{\sigma }$
• 即上图右下侧的示意图

❓❓❓
推理阶段，则只需要卷积网络预测的平移（❓为什么不考虑缩放）参数，❓不用推理标准化流

---

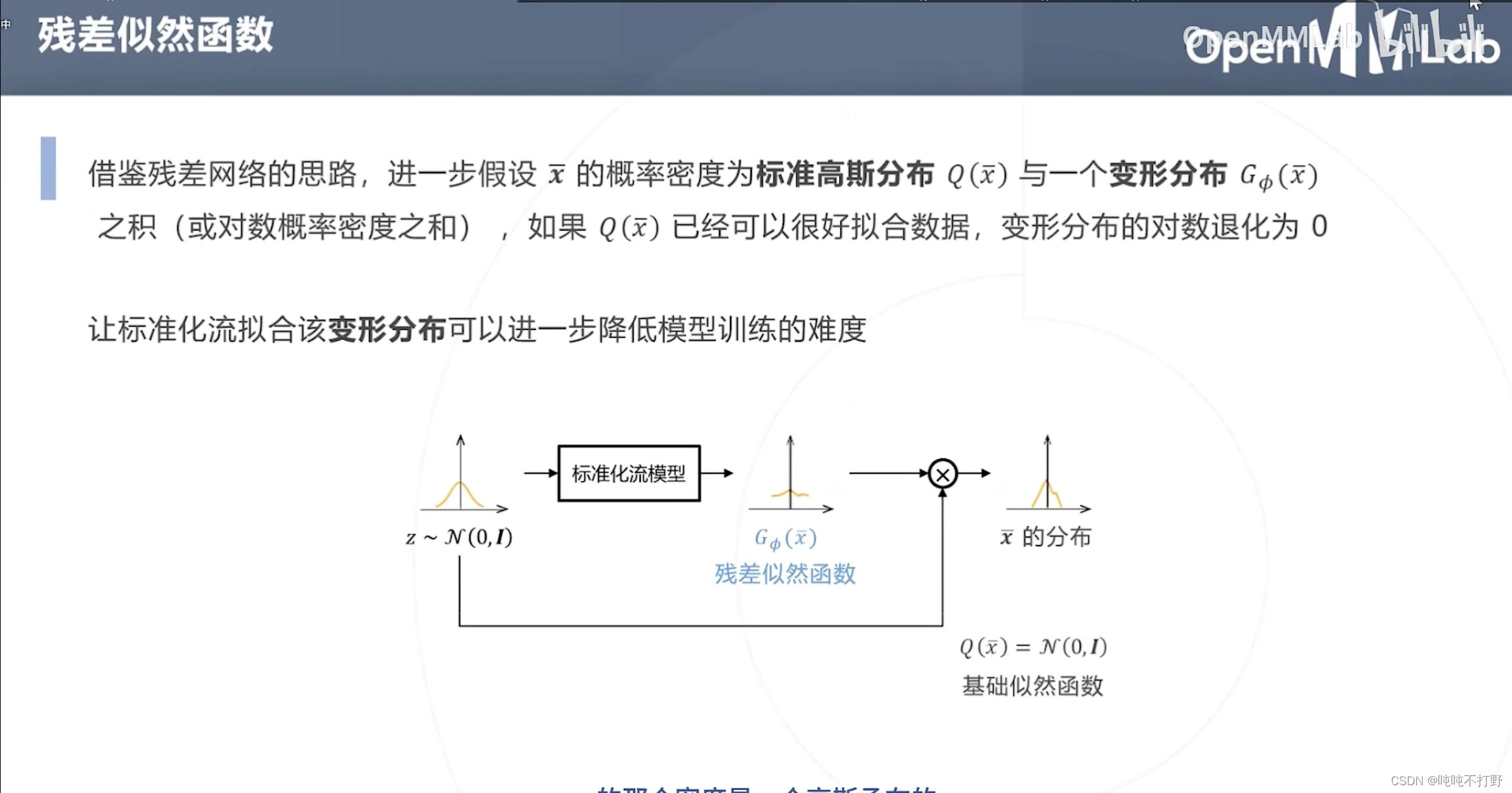
挺好理解的，看ppt就行

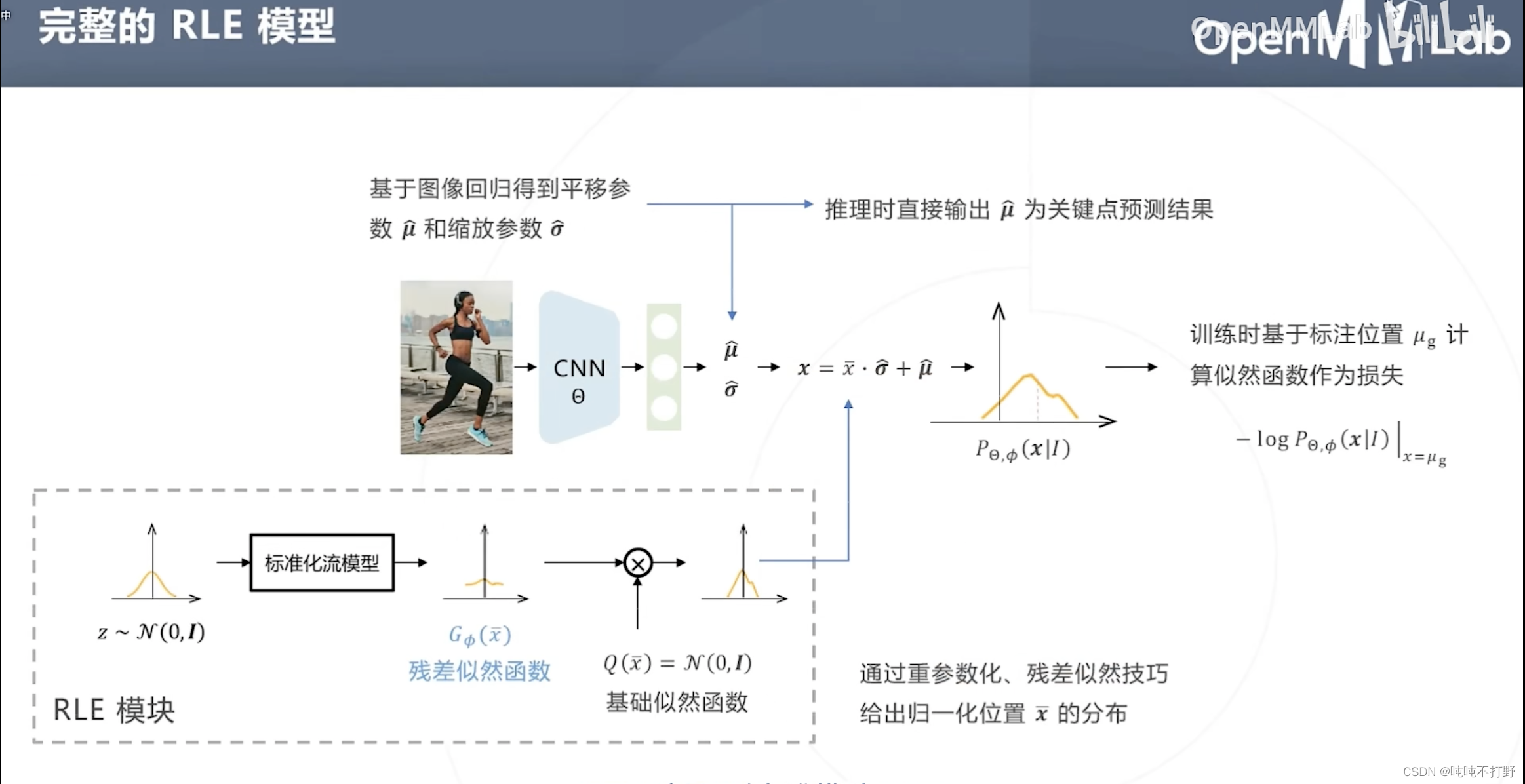
对标准化流模型得到的标准分布，进一步使用残差似然函数，就变成上图了

2.2 基于热力图的自顶向下方法

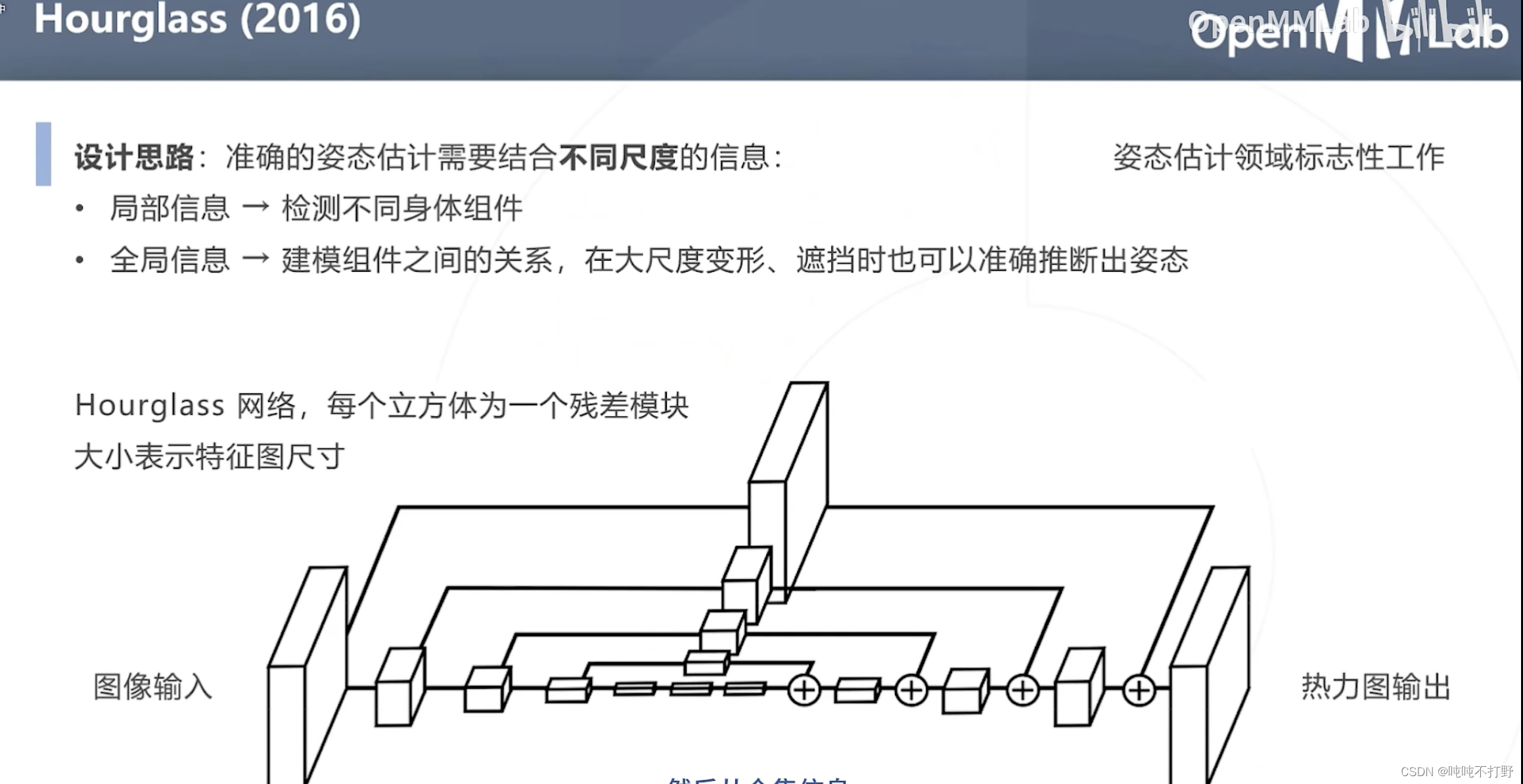
Hourgalss网络，是姿态估计领域标志性的工作

3. 3D姿态估计

4. 人体姿态估计的评估方法

5. DensePose

6. 人体参数化模型