引言
之前面试过一位求职者,其期望薪资是20k,面试时问到了排序算法,结果就是模棱两可,说这说那的…
所以,还是有必要学一些基础算法的
首先,搞明白学算法的重要性和为什么学算法
- 算法我认为是一种解决问题的思路,其不是固定的写法,类似于编程思维。学的算法多了,那么在进行编程时,可以有更多方式去实现特定的功能。比如当你要对很多的数据进行排序时,如果采取的算法合适,其可以让整个排序时间缩短很多倍。
- 很多人都说,我一个搞编程的,搞前端开发的,我不需要学算法。这句话其实我不是很认可。很多人在编程时遇到了技术瓶颈,就连查百度都不知道怎么查。还敢大言不惭说当前技术解决不了遇到的问题。有时候学习到的东西并不是立刻能排上用场,特别是算法。不仅短时间不会使用,时间长了还会忘得干净。那么为什么要学?增长知识点,解决视野盲区。最起码当你遇到那个算法的使用场景时,你能知道原来还有算法可以解决这个问题,而不是一头雾水。
- 不断学习的过程中,也让我学习到了很多的编程知识。比如说常用的流式编程,数位DP算法等。而这些东西,也是不断地能强化自己,我相信,只要坚持学习,到了35岁时,一定不会惧怕裁员。
那么简单的讲讲快速排序算法,这个算法很多科班专业都会学到,但是基本上只有少数爱学习具备一定的编程思维和空间想象能力的人才听得懂。
快排实现步骤
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
- 首先设定一个分界值,通过该分界值将数组分成左右两部分。
- 将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于分界值,而右边部分中各元素都大于或等于分界值。
- 然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
- 重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
排序演示
假设一开始序列{ xi }是:5,3,7,6,4,1,0,2,9,10,8。
此时,ref=5,i=1,j=11,从后往前找,第一个比5小的数是x8=2,因此序列为:2,3,7,6,4,1,0,5,9,10,8。
此时i=1,j=8,从前往后找,第一个比5大的数是x3=7,因此序列为:2,3,5,6,4,1,0,7,9,10,8。
此时,i=3,j=8,从第8位往前找,第一个比5小的数是x7=0,因此:2,3,0,6,4,1,5,7,9,10,8。
此时,i=3,j=7,从第3位往后找,第一个比5大的数是x4=6,因此:2,3,0,5,4,1,6,7,9,10,8。
此时,i=4,j=7,从第7位往前找,第一个比5小的数是x6=1,因此:2,3,0,1,4,5,6,7,9,10,8。
此时,i=4,j=6,从第4位往后找,直到第6位才有比5大的数,这时,i=j=6,ref成为一条分界线,它之前的数都比它小,之后的数都比它大,对于前后两部分数,可以采用同样的方法来排序。
示例代码
public class QuickSort {
public static void main(String[] args) {
int arr[]={3,1,23,3,1,4,5,199,20};
new QuickSort().quickSort(arr, 0, arr.length-1);
for(int i=0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
}
public void quickSort(int[] arr, int start, int end) {
if (start < end) {
int pivot = partition(arr, start, end);
quickSort(arr, start, pivot - 1);
quickSort(arr, pivot + 1, end);
}
}
public int partition(int[] arr, int start, int end) {
int pivot = arr[start];
int left = start + 1;
int right = end;
while (left <= right) {
while (left <= right && arr[left] < pivot) {
left++;
}
while (left <= right && arr[right] >= pivot) {
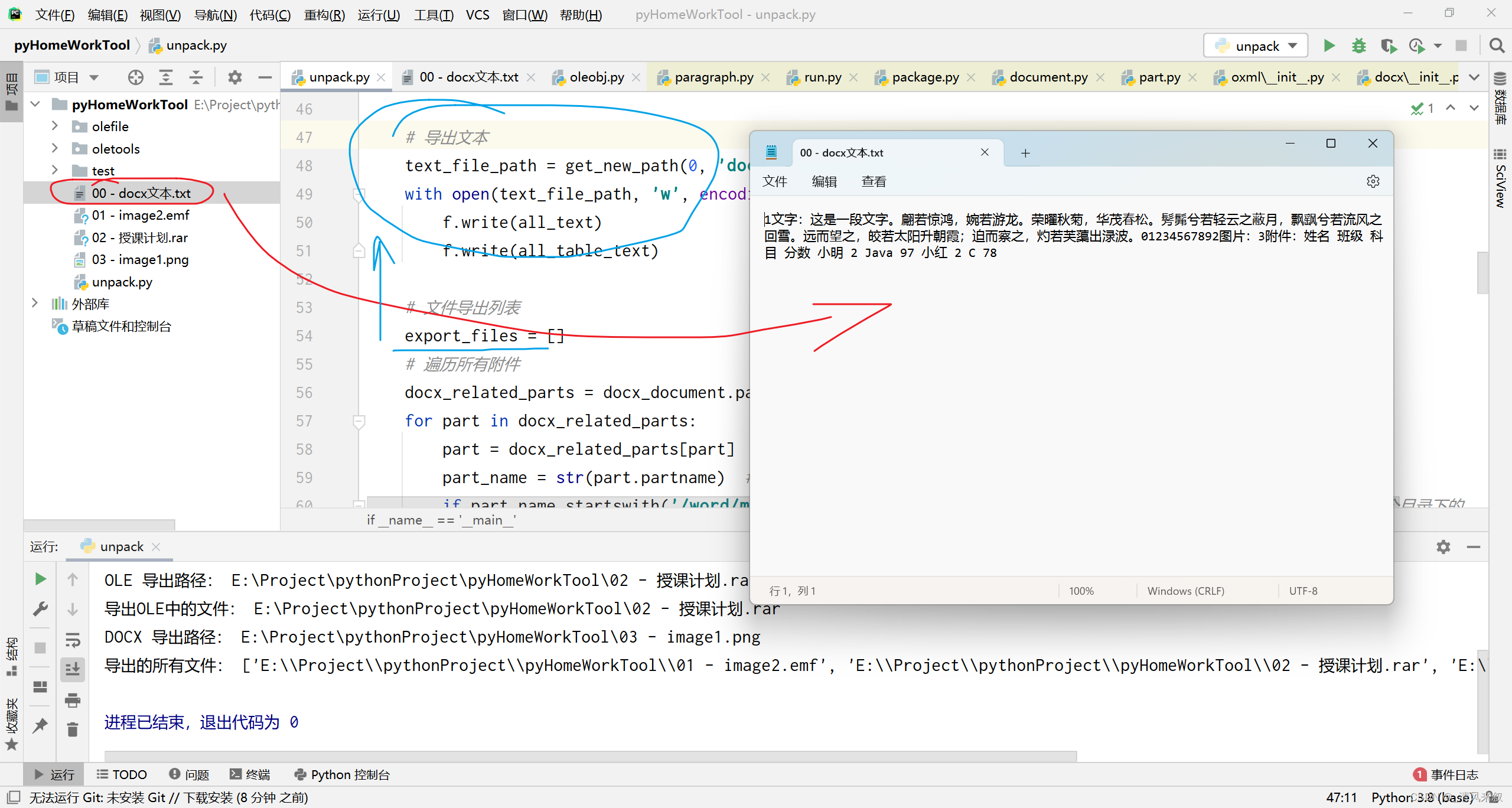
right--;
}
if (left < right) {
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
}
int temp = arr[start];
arr[start] = arr[right];
arr[right] = temp;
return right;
}
}
该算法的思路为选择一个基准元素(通常是第一个元素),然后将数组分为左右两个子数组,左子数组都小于基准元素,右子数组都大于等于基准元素。接着递归地对左右子数组进行排序,最后将左、右子数组和基准元素拼接起来即可。partition 方法用于确定基准元素最终所在的位置。
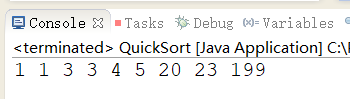
代码运行结果示意:
输入
int arr[]={3,1,23,3,1,4,5,199,20};