H5 Canvas 垂直箭头绘制

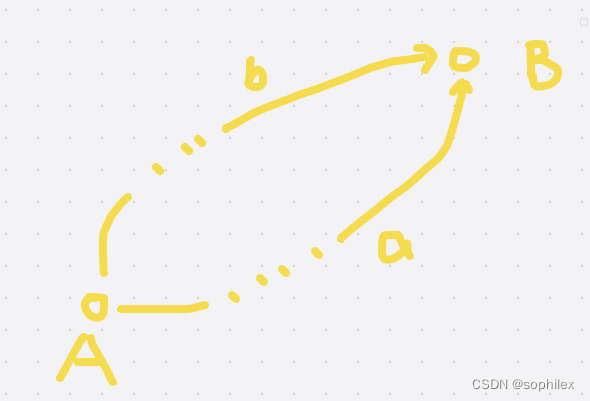
效果

⚠ 因为使用的是斜率来处理的垂直逻辑 tan，当为被除数为0时做了特殊处理，两点自由变换时到达零界点会有卡顿。

推导

开始复习初中二年级数学知识

斜率k的公式： $\dfrac{(y_1 -y_2)}{(x_1 - x_2)}$

两条垂直相交直线的斜率相乘积为-1： $k_1 \times k_2 = -1$

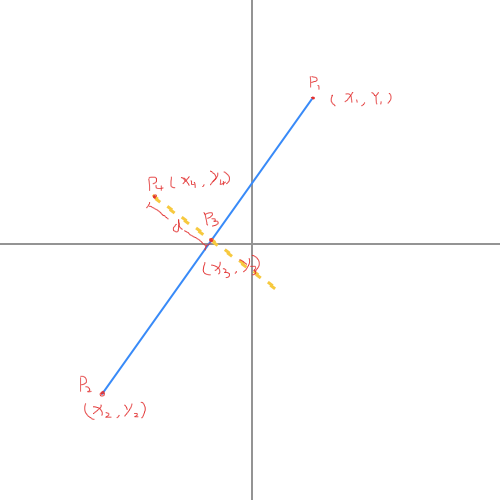
如图已知 $P_1$ 和 $P_2$ 的坐标，以及d的值，求点 $P_4$ 的坐标。 😂怀念初中算题的生活

⚠ 仅个人观点非正确答案

$k_1 \times k_2 = -1$

设：

$P_1P_2$ 的斜率为 $k_1$
$P_3P_4$ 的斜率为 $k_2$

$k_1 = \dfrac{(y_2 -y_1)}{(x_2 - x_1)}$
$k_2 = \dfrac{(y_4 -y_3)}{(x_4 - x_3)}$

$k_1 \times \dfrac{(y_4 -y_3)}{(x_4 - x_3)}=-1$

根据勾股定理可知

$\sqrt{(y_4 -y_3)^2 + (x_4 - x_3)^2}$

可知下列俩公式

$(y_4 -y_3)=\sqrt{d^2 - (x_4 - x_3)^2}$

$(y_4 -y_3)=-\dfrac{ (x_4 - x_3)}{k_1}$

合并继续推

$\sqrt{d^2 - (x_4 - x_3)^2}=-\dfrac{ (x_4 - x_3)}{k_1}$

$d^2 - (x_4 - x_3)^2=\dfrac{ (x_4 - x_3)^2}{k_1^2}$

$\dfrac{ (x_4 - x_3)^2}{k_1^2}+(x_4 - x_3)^2=d^2$

$(x_4 - x_3)^2 \times (\dfrac{1}{k_1^2} + 1)=d^2$

$(x_4 - x_3)^2 =\dfrac{d^2}{\dfrac{1}{k_1^2} + 1}$

可知

$(x_4 - x_3)=\sqrt{\dfrac{d^2}{\dfrac{1}{k_1^2} + 1}}$
$(y_4 - y_3)=-\dfrac{ (x_4 - x_3)}{k_1}$

代码

获取坐标点

将 $x_4$ 和 $y_4$ 套入公式中的 $x_4 - x_3)$ 和 $y_4 - y_3)$

// 已知 A⊥B 则 斜率 k1 * k2 = -1
// 因 k1 = (y2 - y1)/(x2 - x1) 
// 所以 (y4 - y3)/(x4 - x3) = - (y2 - y1)/(x2 - x1) 
let x1 = startX
let y1 = startY
let x2 = endX
let y2 = endY

let k = (y2 - y1) / (x2 - x1)


let y3 = (y1 + y2) / 2
let x3 = (x1 + x2) / 2

// 设 d 为箭头末端距离线的距离
let d = 20;

let x4 = 0
let y4 = 0
if (x1 == x2) x4 = Math.sign(redirect) * d;
else if (y1 == y2) y4 = Math.sign(redirect) * d;
else {
    x4 = Math.sign(redirect) * Math.sqrt(Math.pow(d, 2) / (1 + Math.pow(1 / k, 2)))
    y4 = - 1 / k * x4;
}

其中redirect是指对应方向

绘制箭头

// 获得角度
let a = Math.atan2(y4, x4) * 180 / Math.PI
// 角度偏移值
a += 90
// 角度转弧度
let rd = a * Math.PI / 180
// 保存画布
ctx.save()
// 移动画布
ctx.translate(x4 + x3, y4 + y3)
// 旋转画布
ctx.rotate(rd)
// 绘制箭头
ctx.drawImage(arrowImage, -10, -20, 20, 22)
// 画布还原
ctx.rotate(-rd)
ctx.translate(-x4 - x3, -y4 - y3)
ctx.restore()

源码

<!DOCTYPE html>
<html lang="en">

<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title> 画垂直线</title>

    <style>
        body {
            text-align: center;
        }

        #line {
            width: 600px;
            height: 600px;
            border: 1px solid #ddd;
            margin: 20px auto;
        }
    </style>


</head>

<body>
    <canvas id="line"></canvas>

    <button id="changeRedirect">切换方向</button>

    <script>

        var arrow = `data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMgAAADICAYAAACtWK6eAAAAAXNSR0IArs4c6QAAEoJJREFUeF7tnX+QG+V5x7/P6owNtuG0Og/gUGo4rXCTFFJMJkMmSTHtQPAZSKA1pGX4UULutMIeKAWSlsHOZMiEQCCxTyvs0EKhmbikkBaCsZOZwnQSmgRaaFpS+1YO1Amm4NPKBl9w7ZOejs4uP1wb7ftqdXp399E//OHn++zzfr/vh9XqViuCvMQBceCwDpB4Iw6IA4d3QACR3SEOvIcDAohsD3FAAJE9IA7oOSBnED3fRJUSBwSQlAQty9RzQADR801UKXFAAElJ0LJMPQcEED3fRJUSBwQQg4LuL7/4oYzV+ESzSTvYam4+ytq1ZfvwGb82aMTUjSKA9Djy/rtf7LdmTq4EcDGA3zhonJeZMdqHvaM7Sh/Y3eNRU3l4AaSHsee8LZ9iWC04PtRmjBcY1mjdHbynh+Om8tACSI9iz3ljtzDoS2qHpzsCN3+TmkaqO3FAAOnEPU1tzhtbzqDVenJeF7iFYT2tqFQdEEBUHeuwPlepXsnM93XSholuqxfzt3TSQ7ThHBBAwvkUSVWuUv00Mz8SSTNgWeA634mol7Q5jAMCyDRtjWNW+4N9fdjEwGBUh2RkTqu7J/8sqn7S5/87IIBM066wy2OPgOjTUR/OyuybPz78/lei7iv99jsggEzDTrDLW1aBpj7Ojf5F+Ofg1V99AqsWT0bfXDoKIF3eAxFfdxx6WqL7g2L+qi4vJZXtBZAuxt6N647Djyt/I+lGlAJIN1w90LNb1x2HG5lAK2pufk0Xl5S61gJIlyK3K/5KMFZ1qf1h2zJoSd3NPzHdx03q8QSQLiRrl6uXgHh9F1q3bcmMah/ovB2lfLVtsRS0dUAAaWuRWkH/Pb84zWo2NgI4Tk0ZafUTgessibRjSpsJIBEGn1/tz6z1YSMBZ0XYVqsVg9fU3cIKLbGI3nJAAIlwM+Q832OgGGHLjlrJRXtH9k2JBZDOPZzqkKtUVzDzNyJqF1kbuWjvzEoBpDP/ptR22T8HhNZ1h3F+Tl20Z6wlO0YG/QiWmroWxgUatwSya7eeSM3mE2C83+DZNwUDzw1h2bKGwTMaOZoA0mEstld9GOCLOmzTdTkBlZrruF0/UMIOIIB0EGjW828j4M87aDG9UqYbg1L+zuk9aLyPJoBo5pfz/MsYeFBT3jMZsXVxrTQY1Ze2eraO6TqwAKLh9MA9W89otq47gAENea8l25vMQztLhed7PUgcji+AKKZ07AP/PXvf7tc3AvQxRalB5fRDTPJQsMJ53aChjBxFAFGMxa5U14H5GkWZceUMeqDu5q8wbjDDBhJAFAKxPf9PAXxNQWJ2KWFVUHS+aPaQvZ1OAAnpf3Z0yxKyrMdDlsemjAiX14pO7D5smC6DBZAQTh+zZvNJGSuzEYRCiPK4lbzOREvqxfyP4jb4dMwrgIRwOVvx/54YF4YojWvJ81ZmxpLx4QXydJSDEhRA2mzpnDf2FQbdHNedH35ufiRwC60nzMvrHQ4IIO+xHXJe9QoG35+eHcN3Bm7hxvSst/1KBZDDeJQbHfsIW9T6Y2C2vY3JqWCCWy86leSsqLOVCCCH8M9e7R+NDFoX5Wd2Zm8c1dQA8VBQdDbFcfqoZxZADgVI2f9LEP4karNj1M/PWNaQfIfEwC/49HoTZb2xGwn01V7PYcDxvx+8lh/CKkr1I03lDPKOnZitjC0lpscM2JxmjMC0NijlR8wYpjdTCCAHfJ9XruYniZ8gIN+bKMw8KgOfr7vO7WZO1/2pBJADHtvlscdBJM+SOtSeI1wSFJ2Hur8dzTuCANJ66ELFvwuM682Lx4yJCNgBtoZqpcFnzJho+qZIPSBZb+sIoSmf+7fbc4Sf7t2HpbtXODvalSbp31MNSK5SPZuZW38MPCJJoXZtLYyHgpJzSdf6G9g4tYDYq/0T0IcWHB80MBdjRyLg9prrfN7YASMeLL2AeP7fAZCb8zQ2FDOP1EuFtRrS2ElSCUjW879MwBdil5YxA/MkmIaCkvN9Y0bq0iCpAyRXqV7JzPd1yc80tU3F7SipAsQuVz8KmrooPzpNO7mLa0387SipAWTu2i0DMxqZDQB/uIsbJn2tE347SmoAyVX8v2HGH6dvB3d/xUm+HSUVgNiefysAebxNN1lJ6O0oiQckW6leSszf7ubekN5T35tI5O0oiQZkYNQ/vZmhDWA+VjbxdDhAz8wgLH21mH9tOo42HcdILCDzyi/MadDM1kX5x6fDSDnGWw48HLjOHyTFj8QCYnv+vQCuTkpQsVoH4e6g6LQe0xr7VyIByVaqNxFzar/kY8autK4P3MGvmzGL/hSJAyRXHruIiR7Wt0SUUTlAlnVxbSTeP9aTKECy3uZTCdYGgN4XVcjSpwMHiF61iJaOjww+20GXnkoTA8gJd/3yyIlZezYQcFZPHZWDH+RAvD/ZSgwgtud/E8BnZX8a6UBsP9lKBCByUW4kFAefSe4M3Hzsnvsbe0DkojwOcOyfkRmlesnx4jNxzJ+sKBflcdpqrVmpCcZQUMpvjMvk8T2DrH12ht04pmX02XExW+ac+j/yVkJjaNxduCUOfsQWkKznjxJQioPJMuPBlyP4QWDtGsLwGftM9yaWgOQ8v8TAqOnmynzv5QCvC9zCsOkexQ6QA8+yar21mmG6uTJfWwduCFznrrZVPSyIFSADa186vtmY3AjwqT30TA4dnQN7wPR7QSn/dHQto+0UK0Bsz18PIFVP9os2bvO6MfBUfeC538eyZQ3zpovRx7x2xV8JxioTTZSZOnPA5Kc1xuIM0l/xf8di+iHAR3UWhahNdYAta6g+MrjBtPliAYjtjX0boEtNM0/midABovuDYv6qCDtG0sp4QOShC5HkHIcmEzPmzD321cuPmzBpWOMBsT3/xwA+YpJpMkuXHCD6XFDMt+7KNuZlNCD777XK/JsxbskgXXVg6hMt11nc1YMoNjcbEPluuWKc8S4XQBTzy3r+k/INQUXTYlwugCiGZ5e33ACy7lSUSXlMHRBAFIOzR/0zYcHY2xAUlyPlbRwgpitqpfwDJhll9DVIy6ic5z/KwPkmmSazRO8AAY/VXOeC6Dt31tF4QOau3T7Q15jYSMCizpYqanMd4HUZtu7YUcpXTZvReECmziLlsd9ios+C+VIQzTfNRJlH2YHdAF4C+GkL1rpxN/8vyh2mSRALQP7Pi6PvesHOHDnrEov5VAYvAGEBGAsAzJomv1JwGHqFwYf8OiwBewBMMDBhgSeYMQHwBJDZzRZPWE2aYKs5gaY10Wxyq/ZdLyuDPVZj5rbx5Sduj4uRsQKkU1NbT3wHjpoDNObss3gucXMON6zMO/tSho4EOEfAQOttHQOXdXpc0/Wt9/9NstZZmHyuVjzlZdPnnc75UgWIjrE5r7qcwat1tLHQMF0alPJ/G4tZezCkABLC9P3fZNwXm7cFIZZ0oCQZT2APv171SgEkpGd2ecsqkLUyZLnxZa3H79RcJ2/8oD0eUAAJGcCBs4gPYHZIidllzN8NSoWLzB6y99MJIAoZ2N7YTwFKxO+sE/MttVLhNoXlp7JUAFGI3a5U7wPzlQoSY0ubDSzeudx5ytgBDRlMAFEIIkk3T1oZLBofdv5VYfmpLBVAFGLvX+OfZWXwpILE2NKMZRV2jAy2rqnk9R4OCCAK22Pg9s1zm3MzrytIjC3tm5E57rVrTn7V2AENGUwAUQzC9vxdAI5WlBlXPisze/b24fm/Nm4wwwYSQBQDscv+L0A4SVFmXHngOpJ9iFTEpBAmvbPELvvPgHCGosy4cgEkXCQCSDif3qqyPb/1ZPlzFWXGlQsg4SIRQML59FZVzvO/xcAfKcqMKxdAwkUigITz6a2qrFddTeDlijLjygWQcJEIIOF8evstVkKeMi+AhAteAAnn09uAJOSuXgEkXPACSDifBBBFn5JSLoAoJpmU74XIGSRc8AJIOJ/kDKLoU1LKBRDFJOUMomhYzMsFEMUABRBFw2JeLoAoBiiAKBoW83IBRDHApPzarlykhwteAAnnk/yhUNGnpJQLIIpJyhlE0bCYlwsgigEmBpCBfB+WUUNx+akrF0AUI08MIJOYhRXO/yguP3XlAohi5EkBZFZm1+ztw2fIV27b5C+ApBQQa2bj6PGrF76huPzUlQsgipHbnn8rgC8qyowrbx7Zl9151Uk7jRvMsIEEEMVAsp5/MwFfUZQZV74v05z3xvAp48YNZthAAohiILbnXwfgbkWZceV9ezPHvXadPBerXTACSDuHDvr3bMUvEsNTlBlXbjUa7xtfvjCBv3kSrdUCiKKfdtm/GoR7FWXmlTOdGJTyvzRvMLMmEkAU88h6/mUEPKgoM6680WicvGv5wheNG8ywgQQQxUBsz/9DAA8pyowrzzA5Jv4uuWlGCSCKiQx4/gVN4B8UZcaVW8gsHHdPPuTPPRs3bA8HEkAUzbcr/rlgtJ6uGO+XhQ8EI87P472I7k8vgCh6PFDevLhJmX9UlBlXzmicVncX/sy4wQwbSABRDMQuVz8K4h8pyowrbxJO31l0njNuMMMGEkAUAxnwqoua4GcVZcaVW5b14fGRwdivo9vGCiCKDmcr1Q8S878rykwsPzNwnR+bOJhJMwkgimnMu2er02g2xxRlxpUz0cfqxXzs3yp221gBRNHh/tGf/6ZlzXhJUWZcedPi3905Uvgn4wYzbCABRDGQeeUXjmvQEa8oyowrt5jOHi/lE/GLvd00VwBRdPcY77+yGewNFGXmlTf5nODawg/MG8ysiQQQxTzmr91+1J7GxISizLxypvOCUj7+f/DssrMCiKrBD3HGHq9OqspMq2fw0rpbeNy0uUybRwDRSMT2fNaQGSWxgAvHXedRo4YycBgBRCOUJABCRBfVivnvaiw/VRIBRCPuJAACYFngOt/RWH6qJAKIRtxJAISJPlMv5tdrLD9VEgFEI+5kAILL6kXnWxrLT5VEANGIOwmAkEVX1EbyD2gsP1USAUQj7iQAgiauDq51/kpj+amSCCAacScCEKbPBaX8NzWWnyqJAKIRdxIAYXCx7hbu0Vh+qiQCiEbcSQCEgGtrrlPWWH6qJAKIRtxJAATM1wWlwjc0lp8qiQCiEXciAAFuCFznLo3lp0oigGjEnQRAGHxT3S3cobH8VEkEEI24EwEI4Qv1ohP7n3HQiE9JIoAo2bW/OAmAENEttWL+No3lp0oigGjEnQRAQFgVFJ3Y/1KWRnxKEgFEya7knEEY+HLddf5CY/mpkgggGnEn4gzC+FpQcv5MY/mpkgggGnEnARAmGq0X88s1lp8qiQCiEbft+a8DmKshNUlyb+A615g0kImzCCAaqdie/zKA+RpSYyQMPFh3ncuNGcjQQQQQjWDssr8FhIKG1BwJ4aGg6FxizkBmTiKAaOSS9fxnCVikITVGwsCjdde50JiBDB1EANEIJuv5TxJwlobUJMmmwHU+adJAJs4igGikkgRAGHiq7jqLNZafKokAohG3AKJhWkwlAohGcAKIhmkxlQggGsEJIBqmxVQigGgEJ4BomBZTiQCiEZwAomFaTCUCiEZwAoiGaTGVCCAawdmevwnAORpSYyTyMW+4KASQcD69q8r2qg8DfJGG1BgJAd+ruc75xgxk6CACiEYwWc//awJifqMfrw/cwmc0lp8qiQCiEXe27JeJ4GpITZLI7e4h0hBAQph0cEmuPHY7E92kITVJ8vXAda43aSATZxFANFKxPf86AHdrSM2REH0pKOZvNWcgMycRQDRyGfCqi5rgZzWk5kgInwyKTuvTOHm9hwMCiOb2sD2/DqBfU95jGe/FJM0LVjitrw7LSwCJfg/kPP9RBmL5MSkBj9Vc54LoXUleRzmDaGZqV/yVYKzSlPdUxmSdXy8Ofq+nQ8Tk4AKIZlBzR3+VO8J68ycMDGq26IlMzh5qtgsgan69qzqGn2btBtO5QSn/dAfLTpVUAOkk7lVP9mXnnfATIpzeSZvp0jYbWLxzufPUdB0vCccRQDpMsb/ynwsszjwA0Mc7bNVN+fNEzaW14imt53nJS8EBAUTBrMOV9t/9Yj/NbNxH4E9F0C7KFm8S85paqXBzlE3T1EsAiTDtrFc9D2ieB6bziJCPsLVqq/8gpvWTfbx+17CzVVUs9W87IIB0aTdk12z9beprFAjW8U3m+UR0PJjnM3DEoQ5JwJsAdgO8m1v/JesNajb2hRmPLWsPmLeBM9vQh2314cFtYXRS094BAaS9R1KRYgcEkBSHL0tv74AA0t4jqUixAwJIisOXpbd3QABp75FUpNgBASTF4cvS2zsggLT3SCpS7IAAkuLwZentHRBA2nskFSl24H8B/tsPFAslb2gAAAAASUVORK5CYII=`

        var arrowImage = new Image()

        arrowImage.src = arrow;

        var c = document.getElementById("line");

        var b = document.getElementById('changeRedirect')

        /** @type {CanvasRenderingContext2D} */
        var ctx = c.getContext("2d");
        c.width = c.clientWidth
        c.height = c.clientHeight

        var isDown = false;
        var startX = 0;
        var startY = 0;
        var endX = 0;
        var endY = 0

        var lasttime = +new Date()
        var timeoutId = null
        var interval = 20
        var redirect = 1;

        function rendering() {
            // 节流 
            // 不怎么会 仅供参考
            if (+new Date() - lasttime < interval) {
                if (!timeoutId)
                    timeoutId = setTimeout(() => {
                        rendering()
                        clearTimeout(timeoutId)
                        timeoutId = null
                    }, 100)
                return;
            }
            lasttime = +new Date()
            clearTimeout(timeoutId)
            // 清理画布
            ctx.clearRect(0, 0, c.clientWidth, c.clientHeight);

            ctx.strokeStyle = "rgb(18,150,219)"
            // 开始路径
            ctx.beginPath();
            // 移动点到开始位置
            ctx.moveTo(startX, startY);
            // 连接到结束点
            ctx.lineTo(endX, endY);
            // 结束
            ctx.stroke();

            // 已知 A⊥B 则 斜率 k1 * k2 = -1
            // 因 k1 = (y2 - y1)/(x2 - x1) 
            // 所以 (y4 - y3)/(x4 - x3) = - (y2 - y1)/(x2 - x1) 
            let x1 = startX
            let y1 = startY
            let x2 = endX
            let y2 = endY

            let k = (y2 - y1) / (x2 - x1)


            let y3 = (y1 + y2) / 2
            let x3 = (x1 + x2) / 2

            // 设 d 为箭头末端距离线的距离
            let d = 20;

            let x4 = 0
            let y4 = 0
            if (x1 == x2) x4 = Math.sign(redirect) * d;
            else if (y1 == y2) y4 = Math.sign(redirect) * d;
            else {
                x4 = Math.sign(redirect) * Math.sqrt(Math.pow(d, 2) / (1 + Math.pow(1 / k, 2)))
                y4 = - 1 / k * x4;
            }

            // 获得角度
            let a = Math.atan2(y4, x4) * 180 / Math.PI
            // 角度偏移值
            a += 90
            // 角度转弧度
            let rd = a * Math.PI / 180
            // 保存画布
            ctx.save()
            // 移动画布
            ctx.translate(x4 + x3, y4 + y3)
            // 旋转画布
            ctx.rotate(rd)
            // 绘制箭头
            ctx.drawImage(arrowImage, -10, -20, 20, 22)
            // 画布还原
            ctx.rotate(-rd)
            ctx.translate(-x4 - x3, -y4 - y3)
            ctx.restore()

            // 辅助线
            // 开始路径
            // ctx.beginPath();
            // 移动点到开始位置
            // ctx.moveTo(x3, y3);
            // 连接到结束点
            // ctx.lineTo(x4 + x3, y4 + y3);
            // 结束
            // ctx.stroke();
        }
        c.addEventListener('mousedown', (ev) => {
            // console.log(ev);
            isDown = true;
            ctx.clearRect(0, 0, c.clientWidth, c.clientHeight);

            startX = ev.offsetX;
            startY = ev.offsetY;
            endX = ev.offsetX;
            endY = ev.offsetY
        })
        c.addEventListener('mousemove', (ev) => {
            // console.log(ev);
            if (!isDown) return;
            endX = ev.offsetX;
            endY = ev.offsetY;
            rendering();
        })
        document.addEventListener('mouseup', (ev) => {
            // console.log(ev);
            isDown = false
        })
        b.addEventListener('click', (ev) => {
            redirect *= -1;
            rendering()
        })
    </script>
</body>

</html>