好久没更新了,因为最近p事实在是有点多,让人心烦意乱
还是安安心心打比赛舒服
A,B,C就不讲啦
D - Factorial and Multiple
大意:
给定一个数字k<=1e12,求最小的数字n满足n!%k=0;
思路1:
不难想到对质因数进行处理。对于k的每一个质因数pi,不妨假设k的质因数分解中pi的指数为num,则n!中每一个数字的质因数分解对应的pi的指数和一定>=num,所以只要对每一个质因数贪心求一下它对应的上界,然后总体取最大就好了。复杂度大概是sqrt(k)*log(k)
思路2:二分
二分上界就是k<=1e12,然后judge函数的话,跟上一个思路其实差不多,对指数判一下就好了。
思路1代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,cnt,sum,sd;
void solve()
{
cin>>n;
ll ma=0;
for(ll i=2;(i*i)<=n;++i)
{
if(n%i) continue;
cnt=0;
while(n%i==0)
{
n/=i;
cnt++;
}
sum=0;
while(cnt>0)
{
sum+=i;
sd=sum;
while(sd%i==0)
{
sd/=i;
cnt--;
}
}
ma=max(ma,sum);
}
ma=max(ma,n);
cout<<ma<<endl;
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
solve();
return 0;
}
E - Critical Hit
大意:
给定初始数字n,每次操作有p/100的概率变为n-2,有1-p/100的概率变成n-1,求n<=0的期望次数
思路:
好像是做过的最水的E题了,六七分钟就切了。
就是一个最基础的期望递推
设dp【i】表示数字为i时达到要求的期望次数,考虑到每次最多减少2,可以让n++,这样最终合法状态就是0或者1了。然后向后递推的话,
dp[i]=(dp[i-2]+1)*p/100+(dp[i-1]+1)*(1-p/100)
然后求一个逆元就结束了
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=2e5+10;
const ll mod=998244353;
ll ksm(ll x,ll y)
{
ll ans=1;
while(y)
{
if(y&1) ans=ans*x%mod;
x=x*x%mod;
y>>=1;
}
return ans;
}
ll inv(ll x)
{
return ksm(x,mod-2);
}
ll dp[N];
ll p,n;
void solve()
{
cin>>n>>p;
ll in=inv(100);
n++;
dp[1]=0;dp[0]=0;
for(int i=2;i<=n;++i)
{
dp[i]=((dp[i-2]+1)%mod*p%mod*in%mod+(dp[i-1]+1)%mod*(100-p)%mod*in%mod)%mod;
}
cout<<dp[n]<<endl;
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
solve();
return 0;
}
F - Pay or Receive
大意:
给定一张图,每条边正向走时获得权值dis,反向走时获得权值-dis,q次询问求给定两点之间的最最大权值,如果无法到达输出nan,如果获得权值可以达到无限则输出inf
思路:
首先看nan的情况吧,如果两个点不在一个连通块里面,那么结果显然是nan,所以接下来我们都只考虑连通的情况。
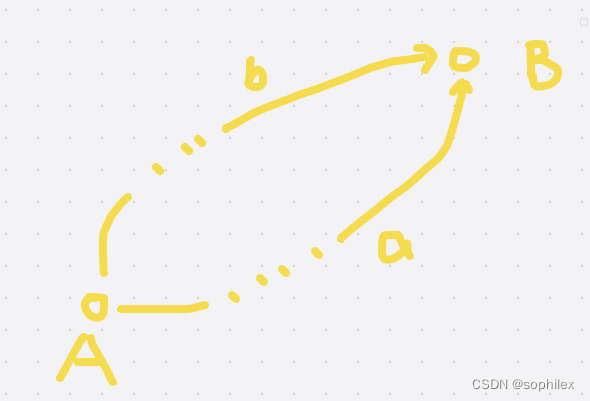
这里,如果A到B有两条路径,且一条的权值为a,另一条的权值为b的话,如果a!=b,那么会发生什么?这就意味着a-b不为0,所以这两条路径产生的环,从某一个方向走的话,总权值就是正的了,那么我们就可以一直走来刷分,那么结果就是inf,考虑到连通块上的其他点也能从环上任意一点到达,所以这整个连通块上的点的答案就都是inf了。
如此我们得到一个结论:从A到B的答案不为inf当且仅当A到B的所有路径的总权值都是相等的,这就是说这里不存在dis更新的问题,因为能更新就意味着inf,这个我们可以在最后直接判掉。
这样的话,我们只用跑一遍dfs,在每一个连通块上随便找一个点以它为根跑一颗生成树为其他点的权值赋值,再判一下哪几个连通块存在路径更新就好了。不是nan也不是inf的话就直接是两点之间的dis之差
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
struct ty
{
ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
void add(ll a,ll b,ll c)
{
edge[++cn].t=b;
edge[cn].l=c;
edge[cn].next=head[a];
head[a]=cn;
}
ll n,m,q;
ll a,b,c;
ll vis[N];
ll dis[N];
ll cnt=0;//连通块数量
ll col[N];//所在连通块
ll wr[N];
void dfs(ll id,ll nu)
{
col[id]=nu;
vis[id]=1;
for(int i=head[id];i!=-1;i=edge[i].next)
{
ll y=edge[i].t;
if(vis[y]) continue;
dis[y]=dis[id]+edge[i].l;
dfs(y,nu);
}
}
void solve()
{
memset(head,-1,sizeof head);
cin>>n>>m>>q;
for(int i=1;i<=m;++i)
{
cin>>a>>b>>c;
add(a,b,c);
add(b,a,-c);
}
for(int i=1;i<=n;++i)
{
if(vis[i]) continue;
dfs(i,++cnt);
}
for(int i=1;i<=n;++i)
{
if(wr[col[i]]) continue;
for(int j=head[i];j!=-1;j=edge[j].next)
{
ll y=edge[j].t;
if(dis[y]!=dis[i]+edge[j].l) wr[col[i]]=1;
}
}
while(q--)
{
cin>>a>>b;
if(col[a]!=col[b])
{
cout<<"nan"<<endl;
continue;
}
if(wr[col[a]])
{
cout<<"inf"<<endl;
continue;
}
cout<<dis[b]-dis[a]<<endl;
}
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
solve();
return 0;
}