摘要
本文为少样本异常检测(FSAD),这是一种实用但尚未被研究的异常检测(AD),少样本意味着在训练中只为每个类别提供有限数量的正常图像。
现有的少样本异常检测的研究主要使用的是 一类别一模型 学习范式,而类别间的共性尚未被探索。
受人类探测异常的启发,将有问题的图像与正常图像进行比较,我们在这里利用配准,这是一种固有可跨类别泛化的图像对齐任务,作为代理任务来训练类别不可知的异常检测模型。在测试过程中,通过比较测试图像的配准特征及其相应的支持(正常)图像来识别异常。
这是一个训练单一、可一般化模型的FSAD方法,并且不需要对新类别进行重新训练或参数微调。
介绍
由于对“异常”的定义比较模糊,即不符合“正常”的样本,都算异常,因此我们不可能用一组详尽的异常样本进行训练。
因此,目前关于异常检测的研究主要是无监督学习。只使用“正常”的样本进行训练,通过使用单类分类、重构或自监督学习任务对正态分布进行建模,得到异常检测模型。
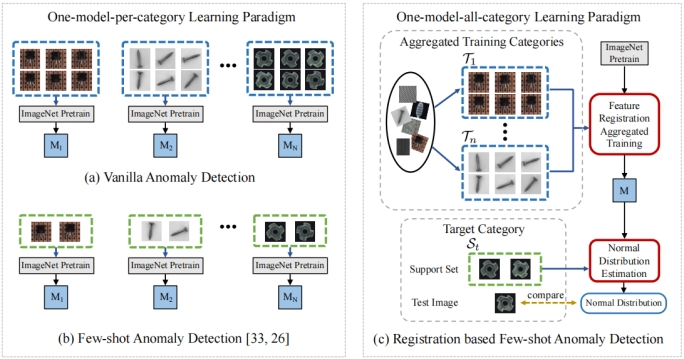
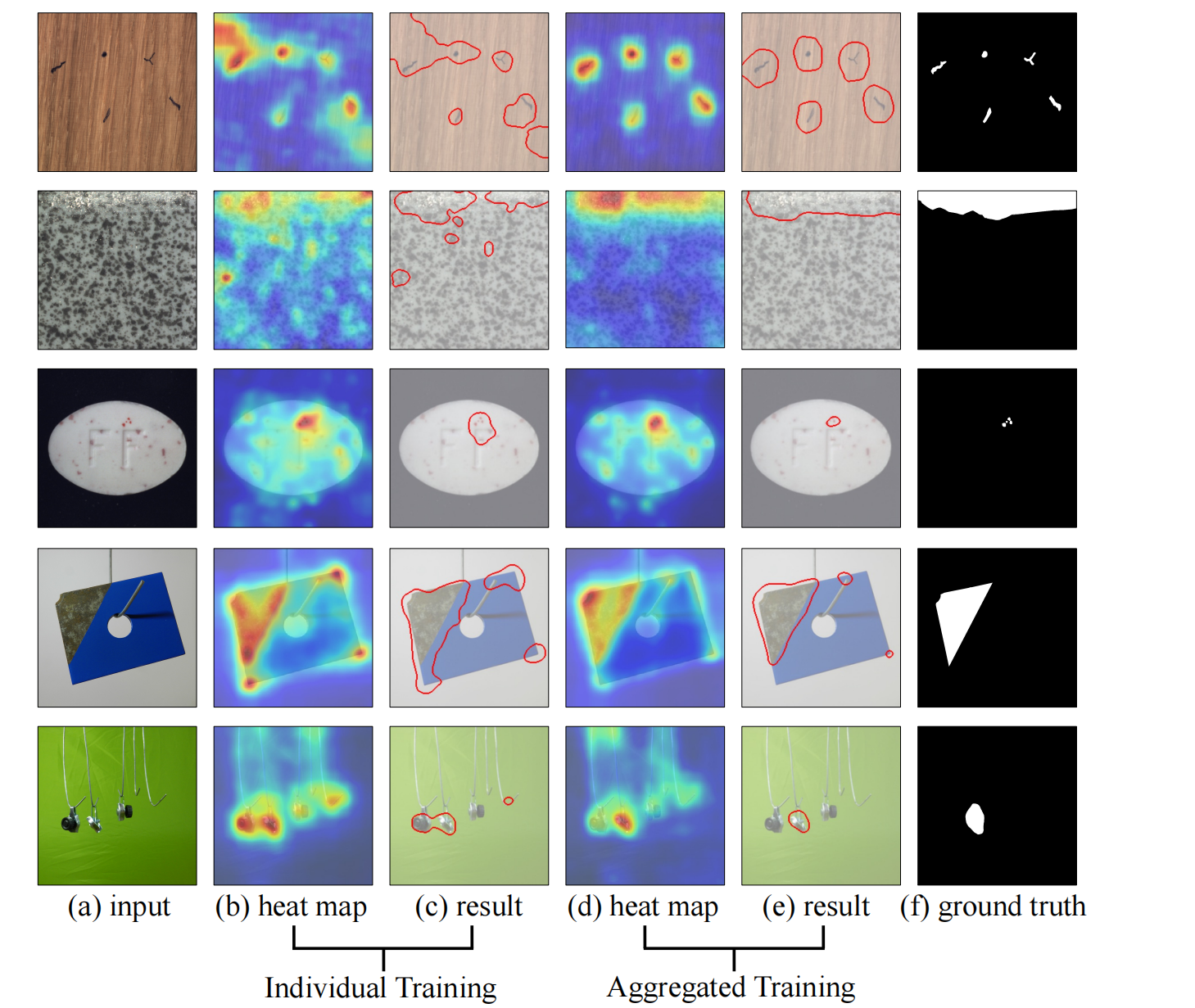
左图是一个异常类别训练一个模型,a需要每个类别都要有大量的训练数据,训练n个模型;b每个类别仅需少量样本,但也要训练n个模型
右图是基于匹配的少样本异常检测,每个类别仅需少量样本,只训练一个模型;
在测试时,为目标类别以及每个测试样本提供了由几个正常样本组成的支撑集(support set),使用基于统计的分布估计器估计目标类别注册特征的正态分布,超出统计正态分布的测试样本被视为异常。
大多数现有的缺陷检测方法大都集中于为每个类别训练一个专门的模型(图a);然而,在缺陷检测等现实场景中,需要处理数百种工业产品,为每个产品收集一个大型训练集并没有成本效益,多个模型推理速度很慢,因此很多对时间敏感的场景应用难以应用。
在训练中只为每个类别提供有限数量的正常图像 (图b),异常检测的少样本学习采用了减少对训练样本需求的策略,如使用多变换的基本数据增强或正态分布估计的较轻估计器。然而,这些方法仍然遵循一个模型一个类别的学习范式,并未能利用类别间的共性。
图1 ©提供了所提出的基于配准的少镜头异常检测(RegAD)框架。受人类如何检测新类别的启发,当一个人被要求搜索图像中的异常时,只需将样本与正常样本进行比较,就可以找到差异进行判断,因此这些图像的实际语义就不再重要了,只需关注差异信息即可。
相关工作
少样本学习:目标是通过一些带注释的例子来适应新的类。具有代表性的少样本方法可以分为度量学习、生成和优化。
- 度量学习方法学习计算一个特征空间,根据其最近的样本类别对一个看不见的样本进行分类。主要是应用siamese net
- 生成方法通过生成新的图像或特征来提高类的性能。
- 优化方法学习不同类别之间的共性,并基于这些共性探索新类的有效优化策略。
- 在本文中,所提出的方法预测了一个新类别的“正常”或“异常”。与之前关于少样本学习的工作相比,训练数据和支持集都只有正常的例子,而没有任何异常的样本。
few-shot 的训练集中包含了很多的类别,每个类别中有多个样本。在训练阶段,会在训练集中随机抽取 N 个类别,每个类别 K 个样本(总共 N x K 个数据),构建一个 meta-task,作为模型的支撑集(support set)输入;再从这 N 个类中剩余的数据中抽取一批(batch)样本作为模型的预测对象(batch set)。即要求模型从 N*K 个数据中学会如何区分这 N 个类别,这样的任务被称为 N-way K-shot 问题。
少样本异常检测:旨在指示异常,只有少数正常样本作为目标类别的支持图像。
TDG 提出了一种分层生成模型,可以捕获每个支持图像的多尺度斑块分布。他们使用多重图像转换和优化鉴别器来区分真实和假补丁,以及应用于补丁的不同转换。异常分数是通过聚合正确转换的基于补丁的投票来获得的。
DiffNe 利用卷积神经网络提取的特征的描述性,使用归一化流来估计它们的密度,这是一个非常适合从少数支持样本中估计分布的工具。
元形成器可以应用于FSAD,尽管在其整个元训练过程中(除了参数预训练之外)应该使用一个额外的大规模数据集MSRA10K,以及额外的像素级注释。
本文设计了基于配准的FSAD来学习类别不可知的特征配准,使模型能够在不调整正常图像的情况下检测新类别的异常。
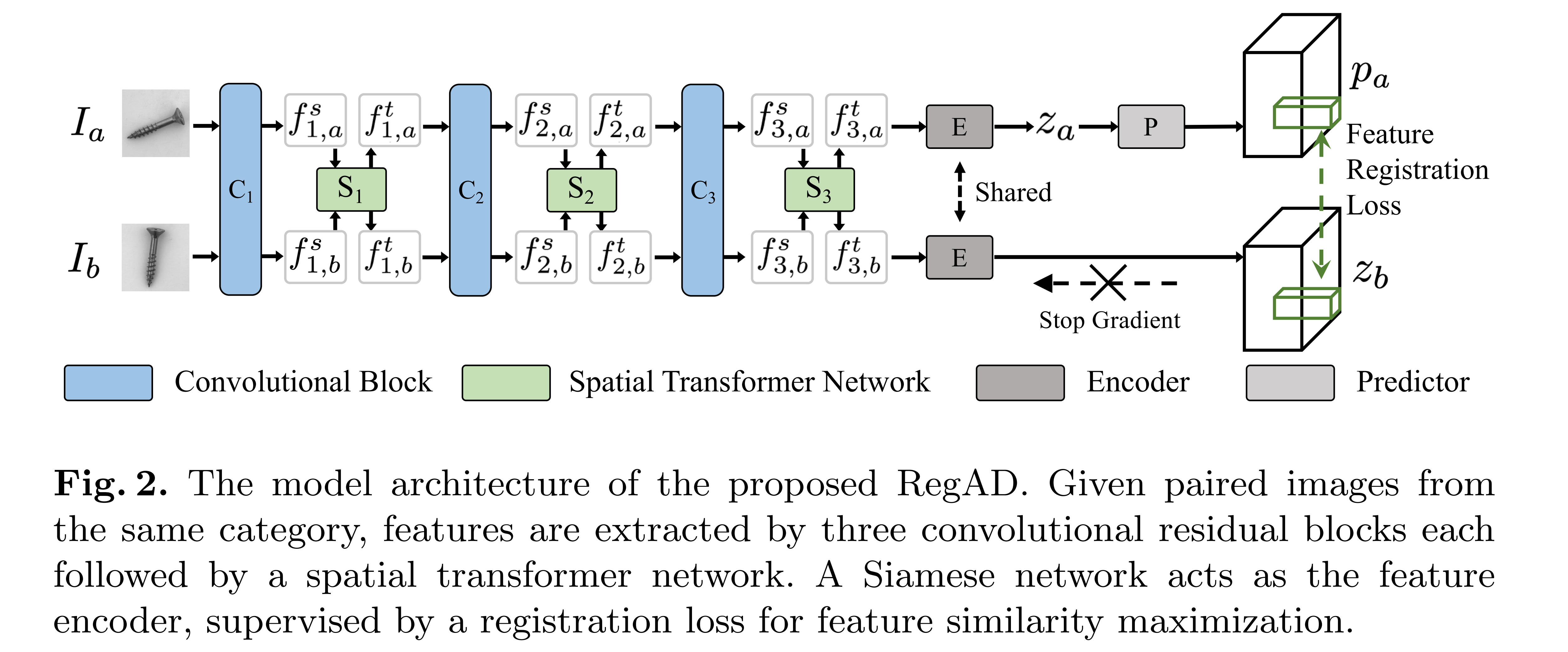
图2.所提出的RegAD的模型体系结构。给定来自同一类别的配对图像,特征由三个卷积残差块提取,每个块后跟一个空间变压器网络。孪生神经网络作为特征编码器,通过配准损失来实现特征相似度最大化。
I a I_a Ia和 I b I_b Ib是同一类的两个图片,先经过 RseNet 和STN的组合进行特征提取;encoder是特征编码器,对卷积得到的特征进行编码(源码中是一系列1x1的卷积和bn层和激活函数的组合,实际相当于全连接层); Z a Z_a Za 原文没说;predictor也是全连接层(1x1卷积)。
利用不同类别的正常图像对模型进行训练:从同一类别中随机选取两幅图像作为训练对,使训练后的匹配模型与类别无关。在测试时,为目标类别提供了少量正常样本的支持集及测试样本。通过比较测试图像的配准特征和相应的支持集图像,可以直接识别异常。
为了更好的鲁棒性,没有使用逐像素配准方法,而是提出了一种通过最大化同一类别特征的余弦相似度来实现特征级配准损失。
基于支持集,利用基于统计的分布估计器估计目标类别的注册特征的正态分布。超出统计正态分布的测试样本被认为是异常的。通过这种方式,该模型通过简单地估计其正态特征分布,而不需要进行任何参数微调,从而快速适应新的类别。
STN空间变形网络
STN(spatial transformer network) 引入了一个新的可学习模块,空间变换器(ST),它可以对网络内的数据进行空间变换操作。这个可微模块可以插入到现有的卷积架构中,使神经网络能够以特征图本身为条件,主动地对特征图进行空间转换,而不需要任何额外的训练监督或对优化进行修改。
STN 能够在没有标注关键点的情况下,根据任务自己学习图片或特征的空间变换参数,将输入图片或者学习的特征在空间上进行对齐,从而减少物体由于空间中的旋转、平移、尺度、扭曲等几何变换对分类、定位等任务的影响。
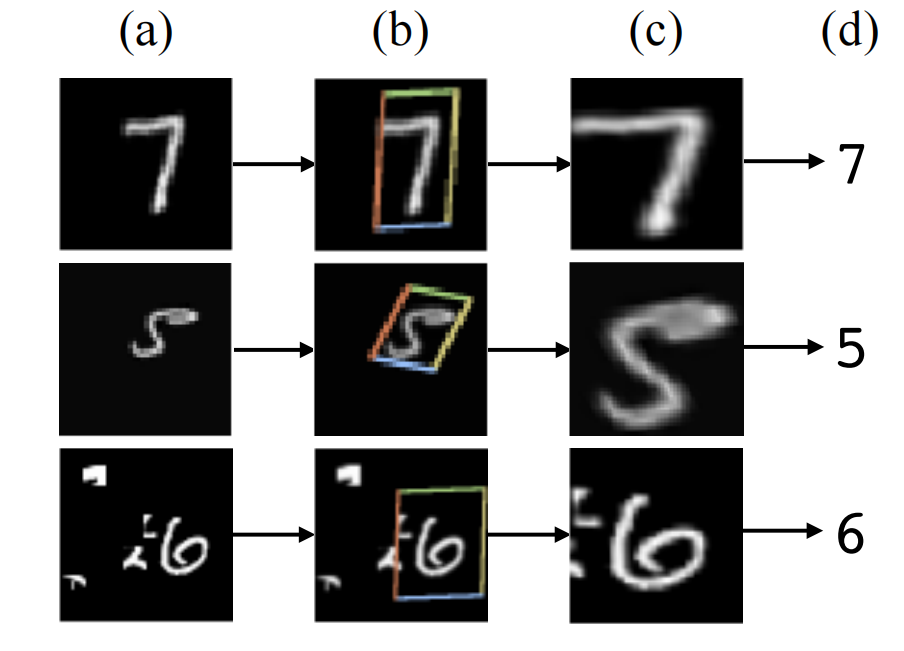
a是输入图片,b 是 STN 中的 localisation 网络检测到的物体区域,c是 STN 对检测到的区域进行线性变换后输出,d 是有 STN 的分类网络的最终输出。
b到c是通过图像的仿射变换(平移、缩放、旋转)得到的
上面几种变换都可以用同一种变换来表示,它一般形式如下:
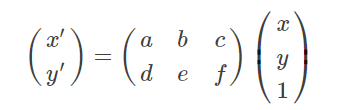
- 当 a = e = 1 , b = c = d = f = 0 a=e=1,b=c=d=f=0 a=e=1,b=c=d=f=0 为恒等变换,即输入图像不变;
- 当 a = e = 1 , b = d = 0 a=e=1,b=d=0 a=e=1,b=d=0时,为平移变换;
- 当 a = c o s θ , b = s i n θ , d = − s i n θ , e = c o s θ , c = f = 0 a=cosθ,b=sinθ,d=−sinθ,e=cosθ,c=f=0 a=cosθ,b=sinθ,d=−sinθ,e=cosθ,c=f=0时,为旋转变换;
- 当 a = e = 1 , c = f = 0 a=e=1,c=f=0 a=e=1,c=f=0时,为剪切变换。
- 当 6 个参数取其他值时,为一般的仿射变换,效果相当于从不同的位置看同一个目标。
STN(spatial transformer network) 更准确地说应该是 STL(spatial transformer layer),它就是网络中的一层,并且可以在任何两层之间添加一个或者多个。
如下图所示,spatial transformer 主要由两部分组成,分别是 localisation net 和 grid generator。
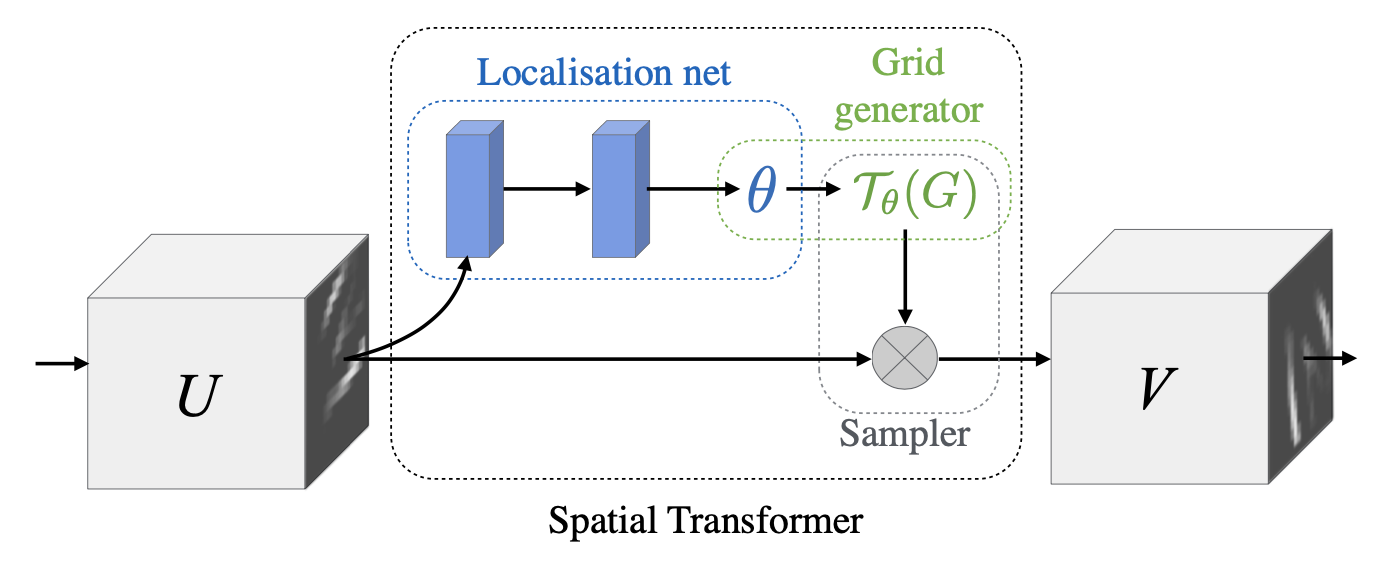
输入的特征图U被位置网络处理得到参数theta,然后经过网格生成器进行放射变换得到采样器,再映射到原图U上,从而得到输出V。
Localisation net
Localisation net的输入feature map长为H,宽为W,通道数目为C
U
∈
R
H
×
W
×
C
U \in {R^{H \times W \times C}}
U∈RH×W×C
经过若干卷积或全链接操作后接一个回归层输出变换参数θ。
θ 的维度取决于网络选择的具体变换类型,如选择仿射变换则 θ ∈ R 2 × 3 \theta\in R^{2\times 3} θ∈R2×3 。
如选择投影变换则 θ ∈ R 3 × 3 \theta\in R^{3\times 3} θ∈R3×3 。θ 的值决定了网络选择的空间变换的”幅度大小”。
Grid generator
Grid generator利用localisation层输出的θ, 对于Feature map进行相应的空间变换,得到一个输出图V,后面会再使用CNN对V进行后续处理(V的尺寸是提前设定的)。
如图 T θ {T_\theta} Tθ作用在U上的一个个点,将U映射为了V这个过程是由Grid generator完成的。
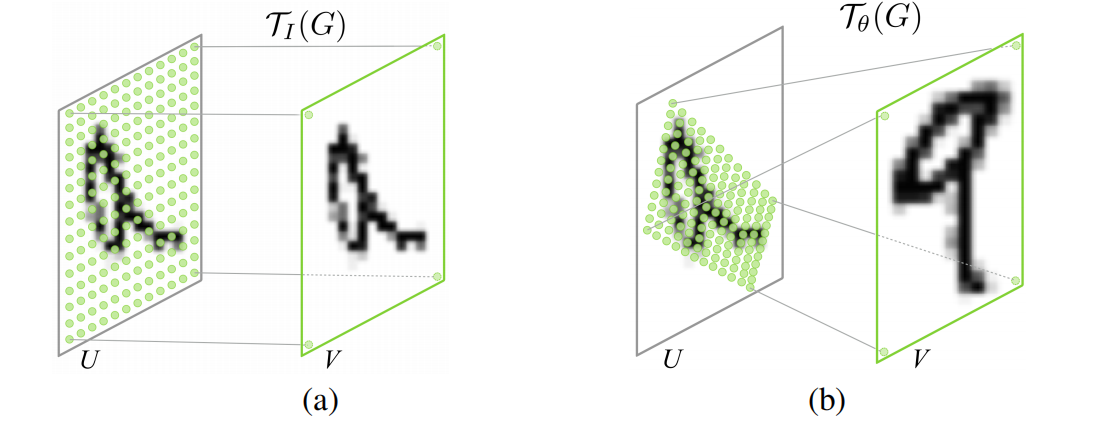
Image Sampler
上面仿射变换只是定义了变换前到变换后的位置映射,这个映射其实并不完整,这就意味着有些点是没有值的,如果要给值,就要使用插值的方法了。论文中提到了最邻近插值和双线性插值两种插值方法。
对于最邻近插值给出了这样的定义:

这样对于输出feature的第i个值,其对应的输入feature的位置取决于m和n,由krnoecker delta函数定义知,当且仅当自变量为0时输出为1.所以上式只有在m取得x方向上距离对应点最近的整数点以及n取得y方向上距离最近的整数点时有值,其值就为对应两个方向都最近的点的值。
双线性插值的基本思想是通过某一点周围四个点的灰度值来估计出该点的灰度值,如图所示.
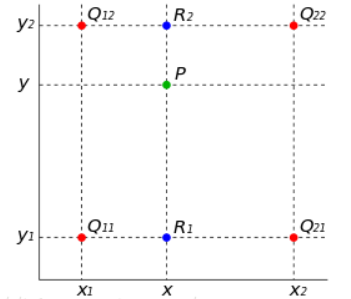
在实现时我们通常将变换后图像上所有的位置映射到原图像计算(这样做比正向计算方便得多),即依次遍历变换后图像上所有的像素点,根据仿射变换矩阵计算出映射到原图像上的坐标(可能出现小数),然后用双线性插值,根据该点周围 4 个位置的值加权平均得到该点值。过程可用如下公式表示:
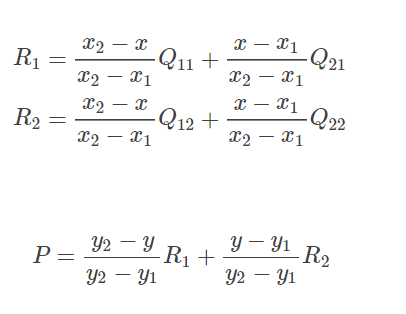
因为 Q 11 , Q 12 , Q 21 , Q 22 Q11,Q12,Q21,Q22 Q11,Q12,Q21,Q22
是相邻的四个点,所以 y 2 − y 1 = 1 , x 2 − x 1 = 1 y2−y1=1,x2−x1=1 y2−y1=1,x2−x1=1,则(13)可化简为:
P = ( y 2 − y ) ( x 2 − x ) Q 11 + ( y 2 − y ) ( x − x 1 ) Q 21 + ( y − y 1 ) ( x 2 − x ) Q 12 + ( y − y 1 ) ( x − x 1 ) Q 22 P=(y_2-y)(x_2-x)Q_{11}+(y_2-y)(x-x_1)Q_{21}+(y-y_1)(x_2-x)Q_{12}+(y-y_1)(x-x_1) Q_{22} P=(y2−y)(x2−x)Q11+(y2−y)(x−x1)Q21+(y−y1)(x2−x)Q12+(y−y1)(x−x1)Q22
论文中对于双线性插值给出了这样的定义:
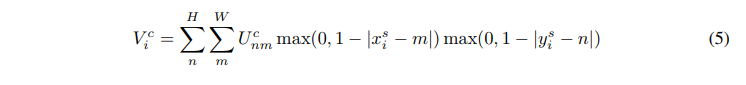
由上式可以知道,只有当m和n取值为对应点xy方向上距离为1以内的整数时才有值,而距离对应点最近的整数点是有四个的,比如(0.5,0.5)距离其最近的四个点分别为(0,0),(0,1),(1,1),(1,0),后面两个取值就成了距离权重,前面U取值为四个点之一的整数点的值,所以这个式子可以解释为以距离作为权重,取最近的四个点的值的加权求和。
反向传播
定义了上面的对应函数,作者证明了输出到输入是可以进行反向传播的,以双线性插值为例:
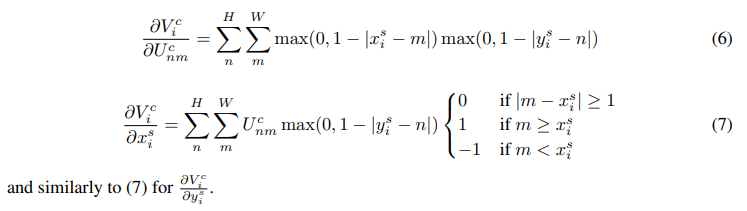
网络搭建
# 导入库
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
from torchsummary import summary
# 加载数据
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 建立模型
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5) # in_channel, out_channel, kennel_size, stride=1, padding=0
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
# Spatial transformer localization-network 只是一个普通的CNN+全连接层
self.localization = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=8, kernel_size=7), # 1*28*28 --> 8*22*22
nn.MaxPool2d(2, stride=2), # 8*22*22 --> 8*11*11
# kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False
nn.ReLU(True),
nn.Conv2d(8, 10, kernel_size=5), # 8*11*11--> 10*7*7
nn.MaxPool2d(2, stride=2), # 10*7*7 --> 10*3*3
nn.ReLU(True)
)
# Regressor for the 3 * 2 affine matrix
self.fc_loc = nn.Sequential(
nn.Linear(10 * 3 * 3, 32), # in_features, out_features, bias = True 10 * 3 * 3 --> 32
nn.ReLU(True),
nn.Linear(32, 3 * 2) # 32-->6 6为仿射变换的六个参数
)
# Initialize the weights/bias with identity transformation
self.fc_loc[2].weight.data.zero_()
self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))
# Spatial transformer network forward function
def stn(self, x): # x: 1*28*28 --> 10*3*3
xs = self.localization(x) # 先进入localization层 1*28*28 --> 10*3*3
xs = xs.view(-1, 10 * 3 * 3) # 展开为向量
theta = self.fc_loc(xs) # 进入全连接层,得到theta向量 10*3*3 -->32 --》 6
theta = theta.view(-1, 2, 3) # 对theta向量进行resize操作,输出2*3的仿射变换矩阵,通道数为C 6--》2*3 仿射变换矩阵为2*3
# affine_grid函数的输入中,theta的格式为(N,2,3),size参数的格式为(N,C,W',H')
# affine_grid函数中得到的输出grid的大小为(N,H,W,2),这里的2是因为一个点的坐标需要x和y两个数来描述
grid = F.affine_grid(theta=theta, size=x.size()) # 这里size参数为输出图像的大小,和输入一样,因此采取 x.size
print(grid.shape) # torch.Size([1, 28, 28, 2])
# grid_sample 函数的输入中,x为输入图,格式为(N,C,W,H),W'可以不等于W,H‘可以不等于H
x = F.grid_sample(x, grid)
print(x.shape) # torch.Size([1, 1, 28, 28])
return x
def forward(self, x):
# transform the input
x = self.stn(x) # 经过仿射变换与采样,得到 1*28*28
# Perform the usual forward pass
x = F.relu(F.max_pool2d(self.conv1(x), 2)) # 1*28*28 --》 10*24*24 --》 10*12*12
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2)) # 10*12*12--》 20*8*8 --》 20*4*4=320
x = x.view(-1, 20*4*4)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x, dim=1)
if __name__ == "__main__":
model = Net()
summary(model, (1, 28, 28), device="cpu")
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 8, 22, 22] 400
MaxPool2d-2 [-1, 8, 11, 11] 0
ReLU-3 [-1, 8, 11, 11] 0
Conv2d-4 [-1, 10, 7, 7] 2,010
MaxPool2d-5 [-1, 10, 3, 3] 0
ReLU-6 [-1, 10, 3, 3] 0
Linear-7 [-1, 32] 2,912
ReLU-8 [-1, 32] 0
Linear-9 [-1, 6] 198
Conv2d-10 [-1, 10, 24, 24] 260
Conv2d-11 [-1, 20, 8, 8] 5,020
Dropout2d-12 [-1, 20, 8, 8] 0
Linear-13 [-1, 50] 16,050
Linear-14 [-1, 10] 510
================================================================
Total params: 27,360
Trainable params: 27,360
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.10
Estimated Total Size (MB): 0.22
----------------------------------------------------------------
特征配准网络(孪生神经网络simsiam )
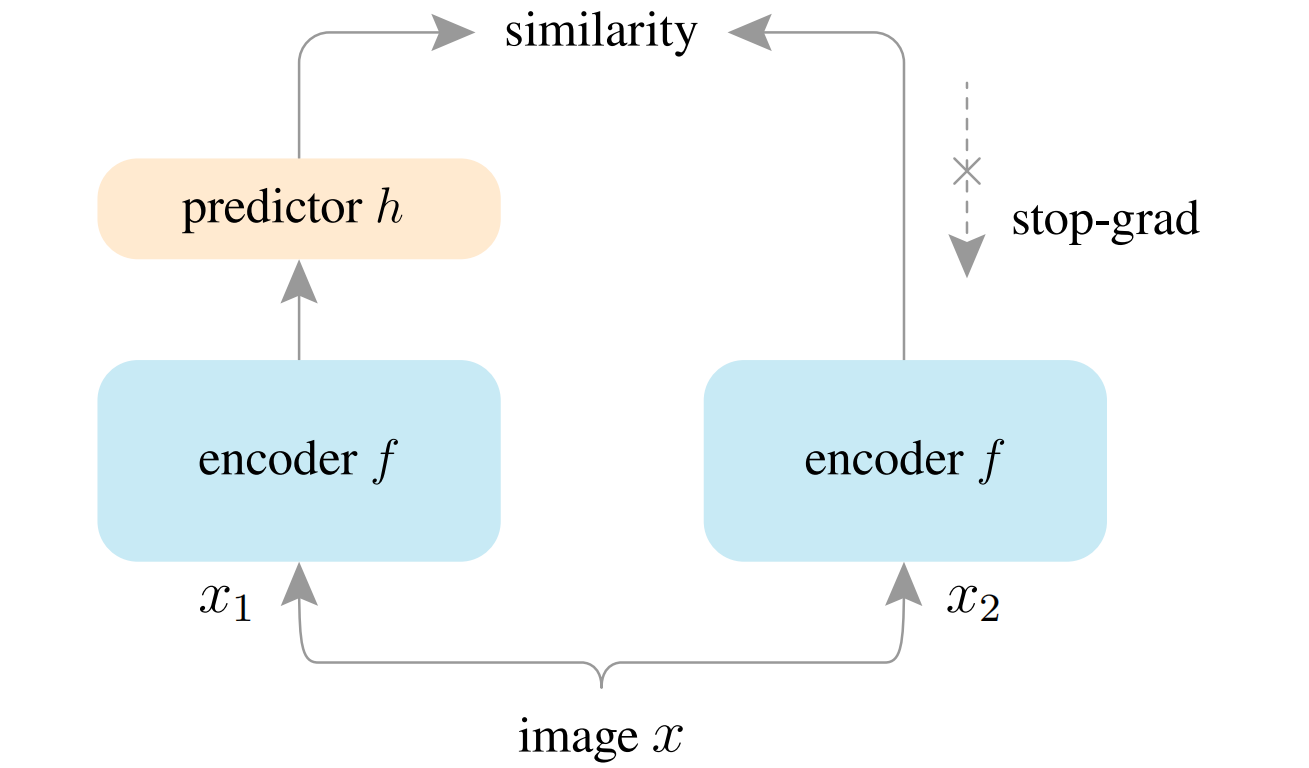
如图为simsiam 的结构,输入是训练集中随机选取的一个图像,使用随机数据增强生成两个图像(同一个图像将其旋转缩放等操作后就有差异了,simsiam要做的就是即使有空间位置上的差异,也能计算出两个图像是否相似);
左右两个encoder是完全一样的,包含卷积和全连接,将图像进行编码(特征提取);
perdictor 是一般的 MLP,左右都是有predictor模块的(看伪代码,只右侧是没画出来),使其对其中一个分支的结果进行变换并与另一个分支的结果进行匹配。该过程可以表示为D(p1, z2),D(p2, z1)(具体看下面伪代码)
用来转换视图的输出,并将其与另一个视图相匹配,(encoder是一样的,x1和x2即使经过数据增强大小也是一样的,那为啥要再加一个predictor模块使两个视图相匹配呢?);
similarity 是对比 predictor 输出的特征向量,loss为经过encoder的输出p和predictor的输出z,p1和z2对比,p2和z1的负余弦相似度 如 D ( p 1 , z 2 ) = − p 1 ∣ ∣ p 1 ∣ ∣ 2 z 2 ∣ ∣ z 2 ∣ ∣ 2 D(p_1,z_2)=-\frac{p_1}{||p_1||_2} \frac{z_2}{||z_2||_2} D(p1,z2)=−∣∣p1∣∣2p1∣∣z2∣∣2z2 (论文中说这个与l2正则化的mse相同?)
总的网络的loss 为 L = D ( p 1 , z 2 ) / 2 + D ( p 2 , z 1 ) / 2 L=D(p_1, z_2)/2 + D(p_2, z_1)/2 L=D(p1,z2)/2+D(p2,z1)/2
# f: backbone + projection mlp
# h: prediction mlp
for x in loader: # load a minibatch x with n samples
x1, x2 = aug(x), aug(x) # random augmentation
z1, z2 = f(x1), f(x2) # projections, n-by-d encodeer的计算
p1, p2 = h(z1), h(z2) # predictions, n-by-d predictor的计算
L = D(p1, z2)/2 + D(p2, z1)/2 # loss 两个向量的负余弦相似度
L.backward() # back-propagate
update(f, h) # SGD update
def D(p, z): # negative cosine similarity
z = z.detach() # stop gradient
p = normalize(p, dim=1) # l2-normalize
z = normalize(z, dim=1) # l2-normalize
return -(p*z).sum(dim=1).mean()
在backward()时,如果y是标量,则不需要为backward()传入任何参数;否则,需要传入一个与y同形的Tensor。
如果不想要被继续追踪,可以调用.detach()将其从追踪记录中分离出来,这样就可以防止将来的计算被追踪,这样梯度就传不过去了。还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来。这种方法在评估模型的时候很常用,因为在评估模型时,我们并不需要计算可训练参数(requires_grad=True)的梯度。
上面将z给detach了, z 2 ∣ ∣ z 2 ∣ ∣ 2 \frac{z_2}{||z_2||_2} ∣∣z2∣∣2z2所以会被看成为常数只有 p 1 ∣ ∣ p 1 ∣ ∣ 2 \frac{p_1}{||p_1||_2} ∣∣p1∣∣2p1会产生梯度。
(D(p1, z2)和D(p2, z1)两个z都被分离出来了,这样岂不是两侧都没法更新了?)
好像应该这样理解: p 1 = h ( z 1 ) = h ( f ( x 1 ) ) p1=h(z1) = h(f(x1)) p1=h(z1)=h(f(x1)),z给detach了,所以只能h求梯度,encoder是不用更新参数的,他只是进行特征提取,提取出来后进入predictor(全连接网络)中,predictor是需要更新参数的,因为他要尽可能的与 z 2 z2 z2 相似(另一个分支也是如此),
从给定的一个由 n n n 个类别的正常样本组成的训练集的同一类别中随机选择一对图像 I a I_a Ia 和 I b I_b Ib,利用ResNet作为特征提取器。如图所示,采用ResNet的前三个卷积残差块 C 1 、 C 2 、 C 3 C_1、C_2、C_3 C1、C2、C3,并丢弃ResNet原始设计中的最后一个卷积块,以确保最终特征仍保留空间信息。
空间变换网络(STN)作为特征变换模块插入每个块中,以使模型能够灵活地学习特征配准。
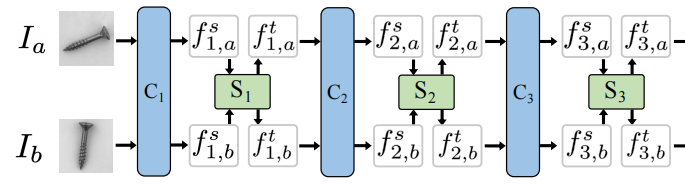
给定成对提取的特征 f 3 , a t f^t_{3,a} f3,at和 f 3 , b t f^t_{3,b} f3,bt作为最终变换输出,将特征编码器设计为应用于多输入的参数共享的孪生神经网络。特征 f 3 , a t f^t_{3,a} f3,at和 f 3 , b t f^t_{3,b} f3,bt 由相同的编码器网络E处理,然后在一个分支上应用预测头P,在另一个分支上停止梯度操作,用来防止崩溃。
表示 p a ≜ P ( E ( f 3 , a ) ) p_a≜ P(E(f_{3,a})) pa≜P(E(f3,a))和 z b ≜ P ( E ( f 3 , b ) ) z_b≜ P(E(f_{3,b})) zb≜P(E(f3,b)) ,采用负余弦相似度损失:
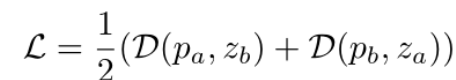
这里使用L2范数的特征级配准损失,而不是逐像素配准图像,这可以被认为是像素级配准约束的松弛版本,以获得更好的鲁棒性。最后,按照SimSiam [5]的方法,将对称特征配准损失定义为:
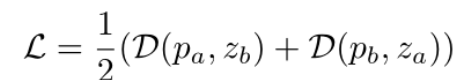
讨论该方法的特征保留了相对完整的空间信息,因为我们采用ResNet的前三个卷积块作为主干,没有全局平均池,然后是卷积编码器和预测器结构,但没有采用SimSiam [5]中的MLP结构。因此等式(3)应该通过平均每个空间像素的余弦相似度得分来计算。包含空间信息的特征有利于AD任务,它需要提供异常得分图作为预测结果。与SimSiam [5]将输入定义为一幅图像的两个增强,并最大化它们的相似性以增强模型表示不同,所提出的特征配准利用两个不同的图像作为输入,并最大限度地提高特征之间的相似性来学习配准。
负余弦相似度
c o s 0 = 1 cos 0=1 cos0=1,两个向量的余弦值越接近1,说明两个向量的夹角越小,两个向量离得越近越相似。
二维空间中,三角形夹角的余弦计算公式为
c
o
s
θ
=
a
2
+
b
2
−
c
2
2
a
b
cos\theta=\frac{a^2+b^2-c^2}{2ab}
cosθ=2aba2+b2−c2
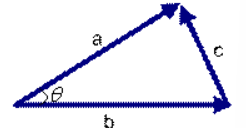
两个向量的余项值计算为:
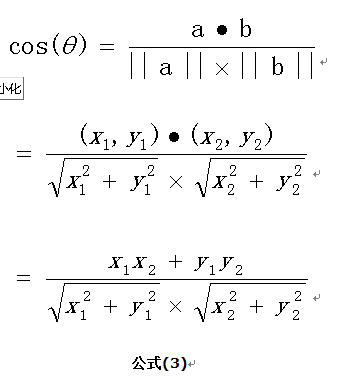
如果向量a和b不是二维而是n维,上述余弦的计算法仍然正确。假定a和b是两个n维向量,a是 ,b是 ,则a与b的夹角 的余弦等于:
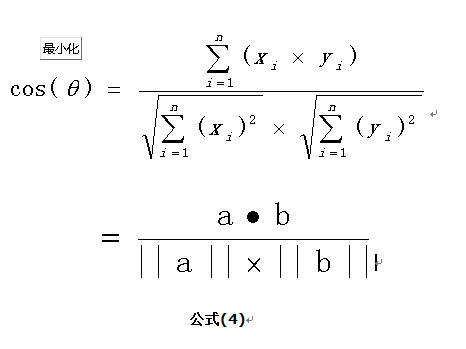
正态分布估计
由于孪生网络的两个分支完全相同,因此仅使用一个分支特征进行正态分布估计。在获得配准特征后,使用基于统计的估计器来估计目标类别特征的正态分布,该估计器使用多元高斯分布来获得正态类的概率表示。
假设图像被划分为 ( i , j ) (i,j) (i,j)的网格位置,估计正态分布的特征的分辨率为 W × H W×H W×H。在每个贴片位置 ( i , j ) (i,j) (i,j),设 F i j = f i j k , k ∈ [ 1 , N ] F_{ij}={f^k_{ij},k∈ [1,N]} Fij=fijk,k∈[1,N]是来自N个增强支持图像的注册特征。 f i j f_{ij} fij是贴片位置(i,j)处的聚合特征,通过将相应位置处的三个STN输出与上采样操作连接以匹配其大小来实现。假设 F i j F_{ij} Fij由 N ( µ i , j , ∑ i j ) N(µ_{i,j},∑_{i_j}) N(µi,j,∑ij)生成,样本协方差为:
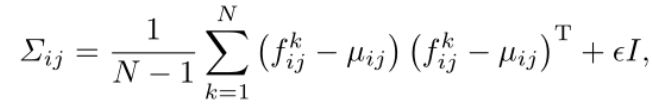
其中 μ i , j \mu_{i,j} μi,j是 F i j F_{i j} Fij的样本平均值,正则化项 ϵ I ϵI ϵI使样本协方差矩阵全秩可逆。最后,每个可能的斑块位置都与一个多元高斯分布相关联。
过程分为两步,因为要希望模型能够预测其它类别的异常,即训练得到的模型不需要微调等操作直接可以拿来使用预测出新的类别的高斯分布,故第一步需要把新的类别的normal数据集输入训练好的模型得到特征值,计算均值和方差得到新类别的高斯分布。第二步则需要输入新类别的测试数据图片,然后利用一定的度量手段来度量该数据输入进网络得到特征图是否满足新类别的高斯分布。
模型得到的特征值
论文中写的是合并三个STN模块输出的特征得到的特征值。注意,因为该特征需要保留原图像的空间信息,所以STN模块输出的特征图需要进行一个逆仿射变换,这样便可以检测出异常像素所在位置。
如何度量:
论文中写的是利用如下公式进行度量, f i j f_{ij} fij是测试图片通过训练好模型得到的特征,均值和方差是测试过程计算得到的均值和方差。经过计算便可以得到对应测试图片每一个像素点的异常分数值,这张地图上的高分表示异常区域。整个图像的最终异常得分是异常图最大值。
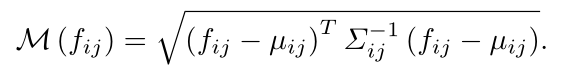
讨论数据增强在AD中被广泛采用,然而,大多数方法只是在支持和测试图像上应用数据增强,而没有探索任何影响。在本文中,我们强调了数据增强在扩展支持集方面起着非常重要的作用,这有利于正态分布的估计。具体来说,我们对支持集S中的每个图像采用了包括旋转、平移、翻转和灰度在内的增强方法 t t t 。我们对支持集中的每个样本进行所有这些增强的可能组合,这些组合联合组合成一个更大的支持集。我们对这样一个增强支持集进行正态分布估计。
推理
在推理过程中,超出正态分布的测试样本被认为是异常的。对于T中的每个测试图像试验,我们使用马氏距离 M ( f i j ) M(fij) M(fij),给位置 ( i 、 j ) (i、j) (i、j)一个异常分数,其中
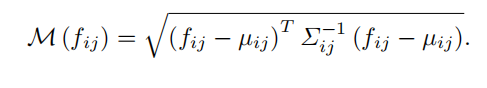
实验结果