3.1 递归

假设你在祖母的阁楼中翻箱倒柜，发现了一个上锁的神秘手提箱。

祖母告诉你，钥匙很可能在下面这个盒子里。

这个盒子里有盒子，而盒子里的盒子又有盒子。钥匙就在某个盒子中。 为找到钥匙，你将使用什么算法?

第一种：

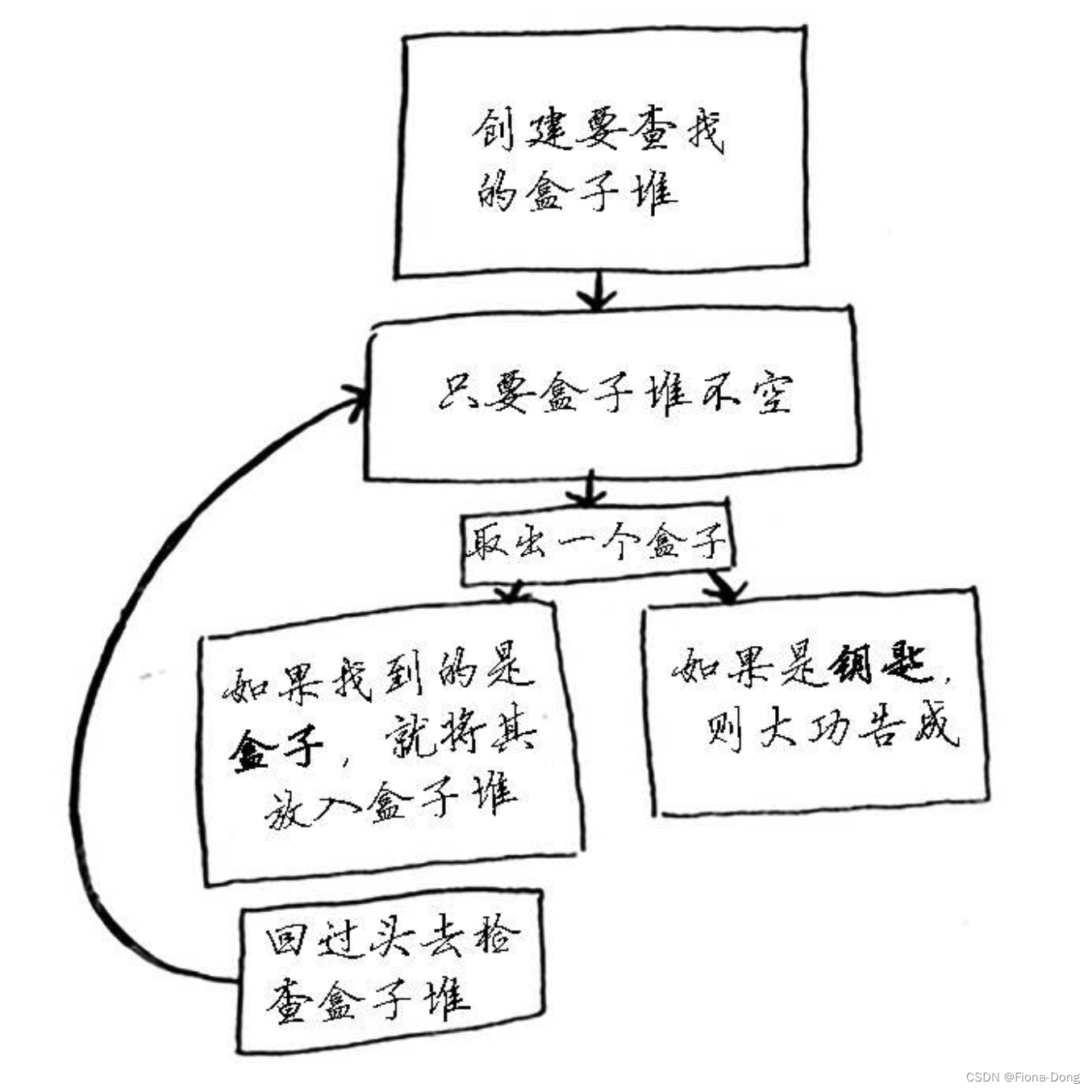
使用的是while循环：只要盒子堆不空，就从中取一个盒子，并在其中仔细查找。

伪码：

def look_for_key(main_box):
	pile = main_box.make_a_pile_to_look_through() while pile is not empty:
	box = pile.grab_a_box() for item in box:
	if item.is_a_box(): 
		pile.append(item)
	elif item.is_a_key(): 
		print "found the key!"

第二种：

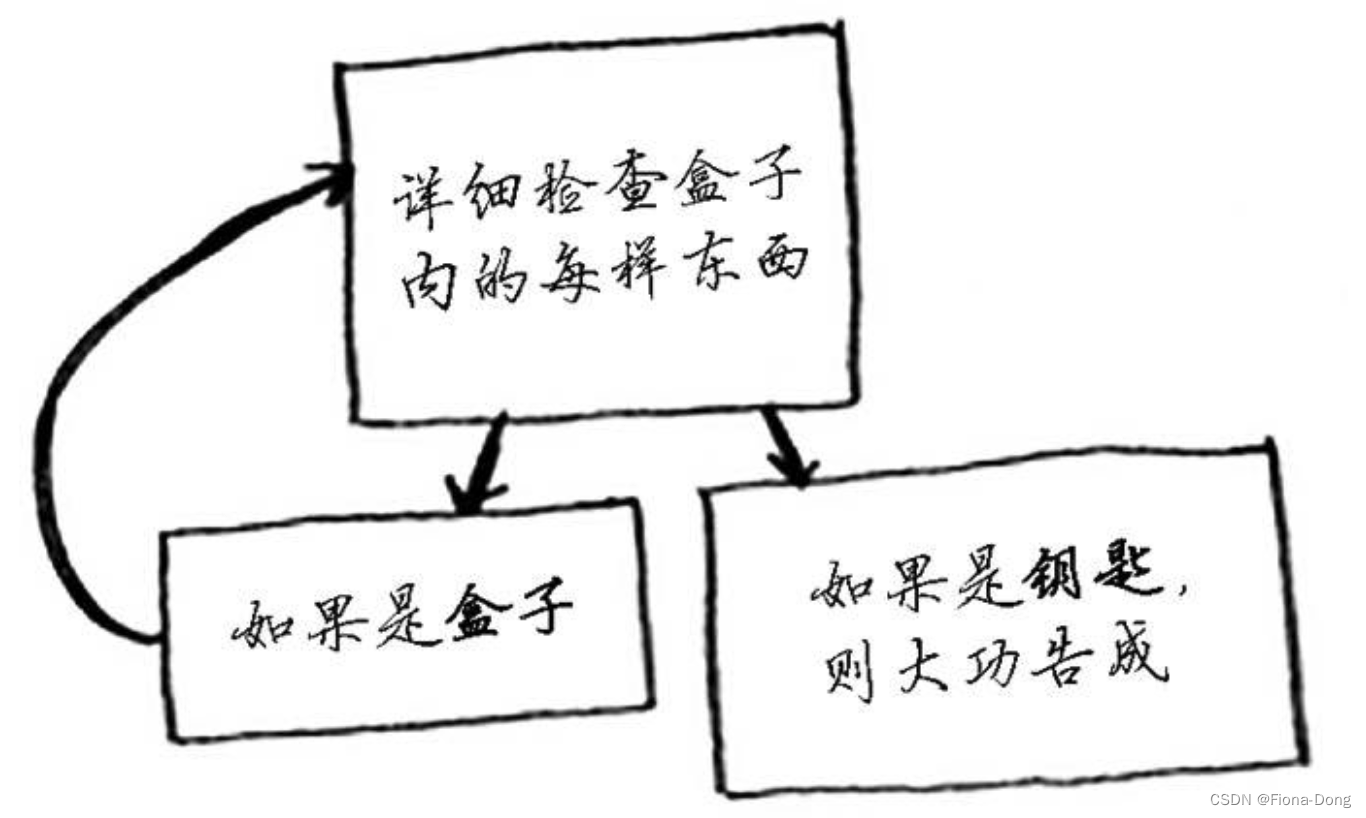
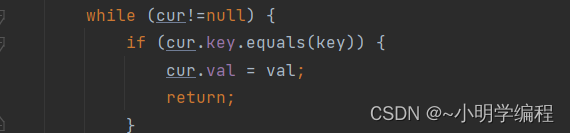
方法使用递归——函数调用自己，伪代码如下：

def look_for_key(box): 
	for item in box:
		if item.is_a_box():
			look_for_key(item) ←------递归! 
		elif item.is_a_key():
			print "found the key!"

第二种方法更清晰。递归只是让解决方案更清晰，并没有性能上的优势。

3.2 基线条件和递归条件

编写递归函数时，必须告诉它何时停止递归。

正因为如此，每个递归函数都有两部分：基线条件 (base case)和递归条件 (recursive case)。

递归条件指的是函数调用自己，而基线条件则指的是函数不再调用自己，从而避免形成无限循环。

编写一个像下面这样倒计时的函数。

3…2…1

def countdown(i): 
	print i
	if i <= 0: ←------基线条件 
		return
	else: ←------递归条件 
		countdown(i-1)

3.3 栈

假设你去野外烧烤，并为此创建了一个待办事项清单——一叠便条：
插入的待办事项放在清单的最前面;读取待办事项时，你只读取最上面的那个，并将其删除。

因此这个待办事项清单只有两种操作: 压入 (插入)和弹出 (删除并读取)。

这种数据结构称为栈 。

3.3.1 调用栈

这个栈用于存储多个函数的变量，被称为调用栈 。

3.3.2 递归调用栈

下面是计算阶乘的递归函数。

def fact(x): 
	if x == 1: 
		return 1
	else:
		return x * fact(x-1)

下面来详细分析调用fact(3) 时调用栈是如何变化的。

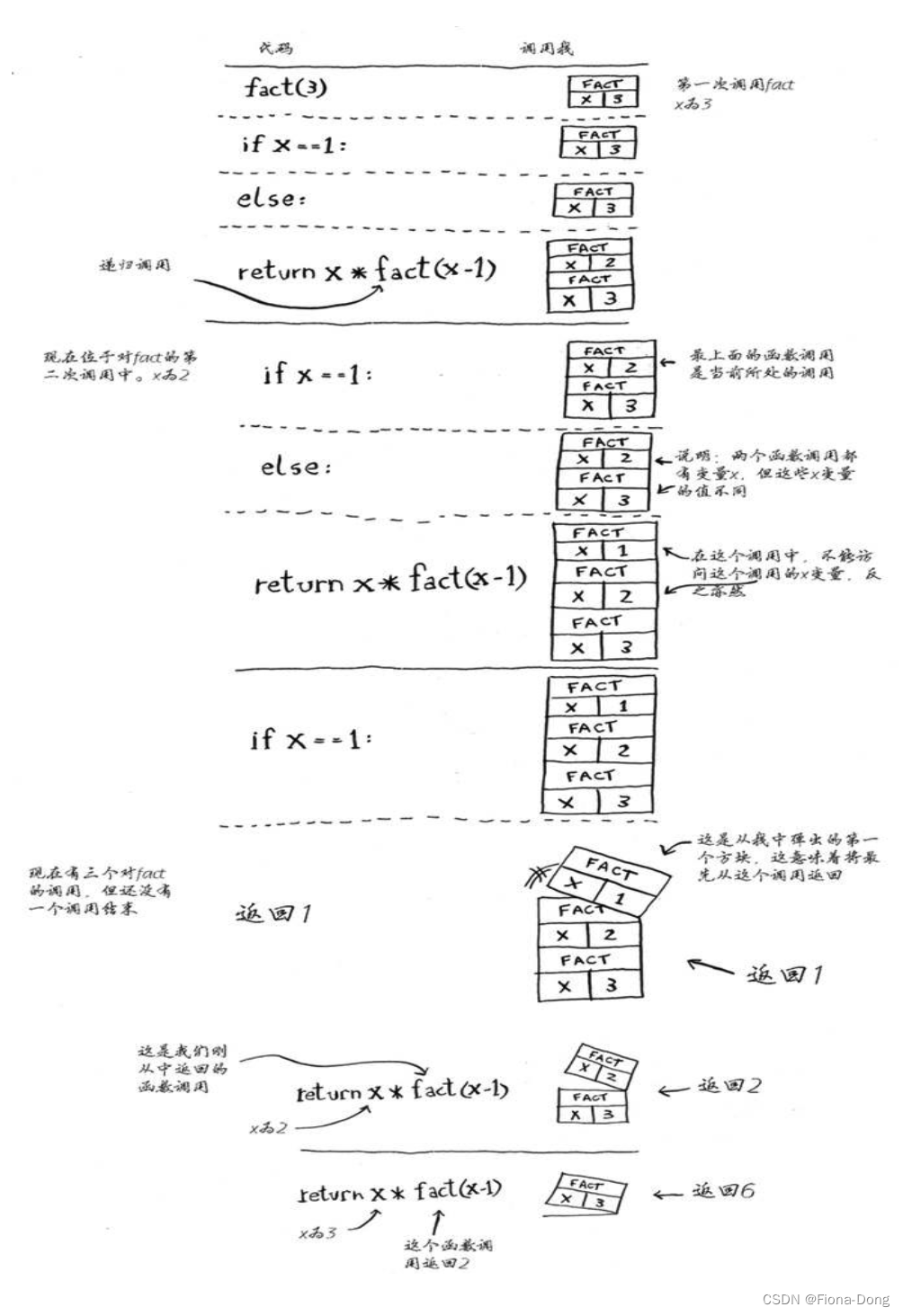
注意，每个fact 调用都有自己的x变量。在一个函数调用中不能访问另一个的x变量。

使用栈虽然很方便，但是也要付出代价:存储详尽的信息可能占用大量的内存。

每个函数调用都要占用一定的内存，如果栈很高，就意味着计算机存储了大量函数调用的信息。在这种情况下，你有两种选择：

重新编写代码，转而使用循环。
使用尾递归 。这是一个高级递归主题，不在本书的讨论范围内。 另外，并非所有的语言都支持尾递归。

References:
《 算法图解》—— 第3章 递归