503.下一个更大元素II

力扣题目链接/文章讲解

视频讲解

本题和739.每日温度很相似，只不过是循环数组

一种处理循环的方式是，直接把两个数组拼接在一起，然后使用单调栈求下一个最大值

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        // 拼接一个新的nums
        vector<int> nums1(nums.begin(), nums.end());
        nums.insert(nums.end(), nums1.begin(), nums1.end());
        // 用新的nums大小来初始化result
        vector<int> result(nums.size(), -1);
        if (nums.size() == 0) return result;

        // 开始单调栈
        stack<int> st;
        st.push(0);
        for (int i = 1; i < nums.size(); i++) { 
            if (nums[i] < nums[st.top()]) st.push(i); 
            else if (nums[i] == nums[st.top()]) st.push(i);
            else { 
                while (!st.empty() && nums[i] > nums[st.top()]) {    // 千万别忘了判断st非空
                    result[st.top()] = nums[i];
                    st.pop();
                }    // 弹出所有比入栈元素小的栈顶元素
                st.push(i);    // 然后再入栈，这样能保持栈顶到栈底元素单调递增
            }
        }
        // 最后再把结果集即result数组resize到原数组大小
        result.resize(nums.size() / 2);
        return result;
    }
};

另一种处理这种循环的方式是，利用取余 % 模拟循环

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        vector<int> ans(nums.size(), -1);
        stack<int> st;
        st.push(0);
        for (int i = 1; i < 2 * nums.size() - 1; ++i) {    // 2*nums.size()-1就相当于遍历数组两次
            int index = i % nums.size();
            if (nums[index] <= nums[st.top()])
                st.push(index);
            else
            {
                while (!st.empty() && nums[index] > nums[st.top()]) {    // 注意判非空
                    ans[st.top()] = nums[index];    // 出栈时记录结果在下标位置
                    st.pop();
                }
                st.push(index);    // 这个时候再入栈不会破坏单调性
            }
        }
        return ans;
    }
};

注意，我们单调栈中存的是下标，单调性看的是下标所对应的值

为什么不直接存值？因为如果存值，出栈的时候需要记录，此时没办法通过这个值确定应该记录在哪个下标位置；而如果存下标，出栈的时候需要记录，可直接通过下标确定应该记录在哪个位置，也能通过下标获取值

42.接雨水

力扣题目链接/文章讲解

视频讲解

本题怎么求能接的雨水？可以看出每一列雨水的高度，取决于，该列左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度

大致过程如下

找到每一列右侧最高的柱子
找到每一列左侧最高的柱子
遍历每一列，用每一列两侧最高柱子的最小值减去该列高度，就是该列能接的雨水

这样一列一列算的代码逻辑如下

class Solution {
public:
    int trap(vector<int>& height) {

        if (height.size() <= 2) return 0;

        vector<int> maxLeft(height.size());
        vector<int> maxRight(height.size());

        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i < maxLeft.size(); i++) {
            maxLeft[i] = max(height[i], maxLeft[i - 1]);
        }

        // 记录每个柱子右边柱子最大高度
        maxRight.back() = height.back();
        for (int i = maxRight.size() - 2; i >= 0; i--) {
            maxRight[i] = max(height[i], maxRight[i + 1]);
        }

        // 求和
        int sum = 0;
        for (int i = 1; i < height.size() - 1; i++) {   // 首尾列不接雨水
            int count = min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) sum += count;
        }
        
        return sum;
    }
};

本题也可以用单调栈解法！单调栈是寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置

放在本题中，通过单调栈能够一行一行算所接的雨水量

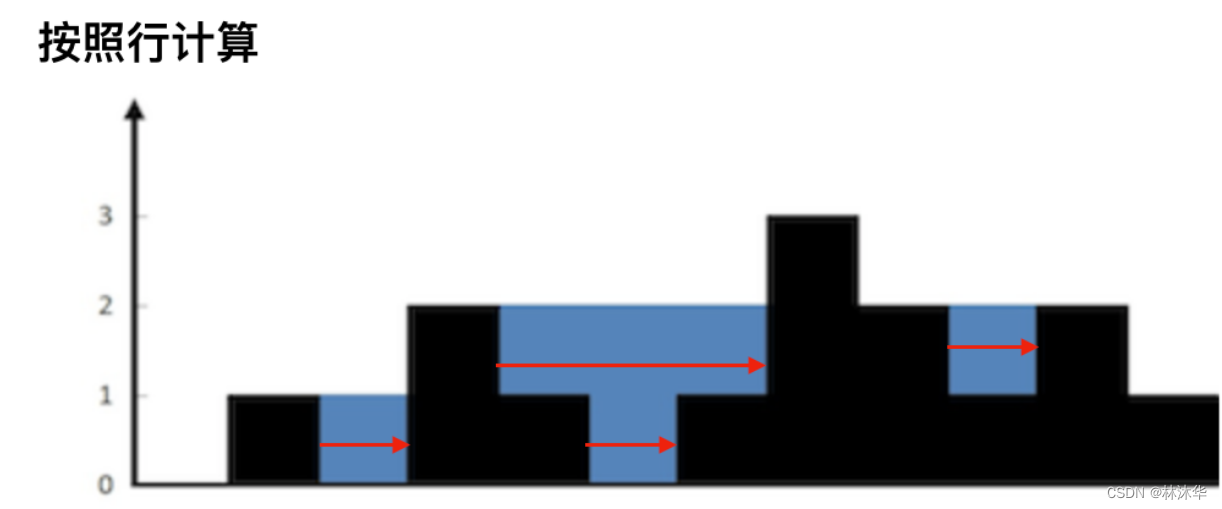
从图中可以看出，一行一行计算，需要知道这一行雨水的高度和宽度

雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度

雨水的宽度是凹槽右边的下标 - 凹槽左边的下标 - 1（因为只求中间宽度）

单调栈处理逻辑和之前的题目差不多，只不过入栈时涉及到出栈的时候记录操作稍微难了点

我们需要关注

凹槽底部高度就是栈顶元素
凹槽右边的高度就是待入栈元素
凹槽左边的高度就是栈顶的下一个元素

代码如下

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0; // 可以不加
        stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度
        st.push(0);
        int sum = 0;
        for (int i = 1; i < height.size(); i++) {
            if (height[i] <= height[st.top()]) {
                st.push(i);
            } else {
                while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
                    int mid = st.top(); // 凹槽底部高度
                    st.pop();
                    if (!st.empty()) {
                        int h = min(height[st.top()]/*凹槽左边高度*/, height[i]/*凹槽右边高度*/) - height[mid]; 
                        int w = i - st.top() - 1; // 注意减一，只求中间宽度
                        sum += h * w;
                    }
                }
                st.push(i);
            }
        }
        return sum;
    }
};

本题也多看视频模拟过程