SimSiam

Abstract

模型坍塌，在siamese中主要是输入数据经过卷积激活后收敛到同一个常数上，导致无论输入什么图像，输出结果都能相同。

而He提出的simple Siamese networks在没有采用之前的避免模型坍塌那些方法：

• 使用负样本
• large batches
• momentum encoders(论文直接用的encoder)

实验表明对于损失和结构确实存在坍塌解，但stop-gradient操作在防止坍塌方面起着至关重要的作用。

Method

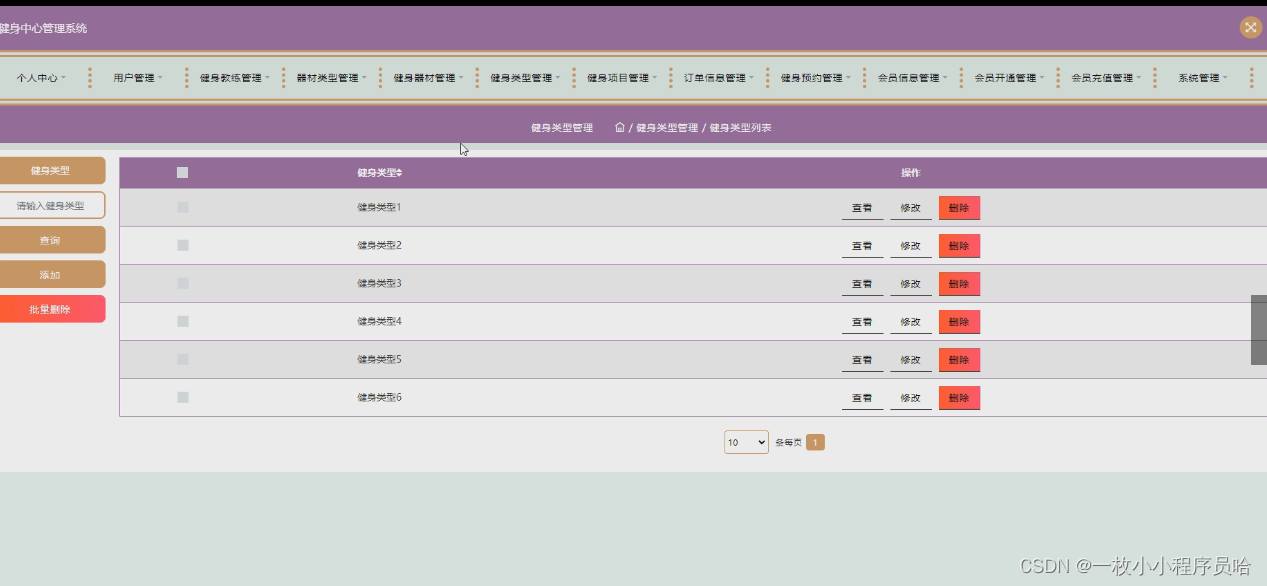
如图为simsiam 的结构，输入是训练集中随机选取的一个图像，使用随机数据增强生成两个图像；左右两个encoder是完全一样的，包含卷积和全连接，将图像进行编码（特征提取）；perdictor 是一般的MLP，左右都是有predictor模块的（看伪代码），只右侧是没画出来，用来转换视图的输出，并将其与另一个视图相匹配，(encoder是一样的，x1和x2即使经过数据增强大小也是一样的，那为啥要再加一个predictor模块使两个视图相匹配呢？)；

similarity是对比predictor输出的特征向量，loss为经过encoder的p和predictor的输出z，p1和z2对比，p2和z1的负余弦相似度 如 $D(p_1,z_2)=-\frac{p_1}{||p_1|{|}_2}\frac{z_2}{||z_2|{|}_2}$ （论文中说这个与l2正则化的mse相同？）

总的网络的loss 为 $L=D(p_1,z_2)/2+D(p_2,z_1)/2$

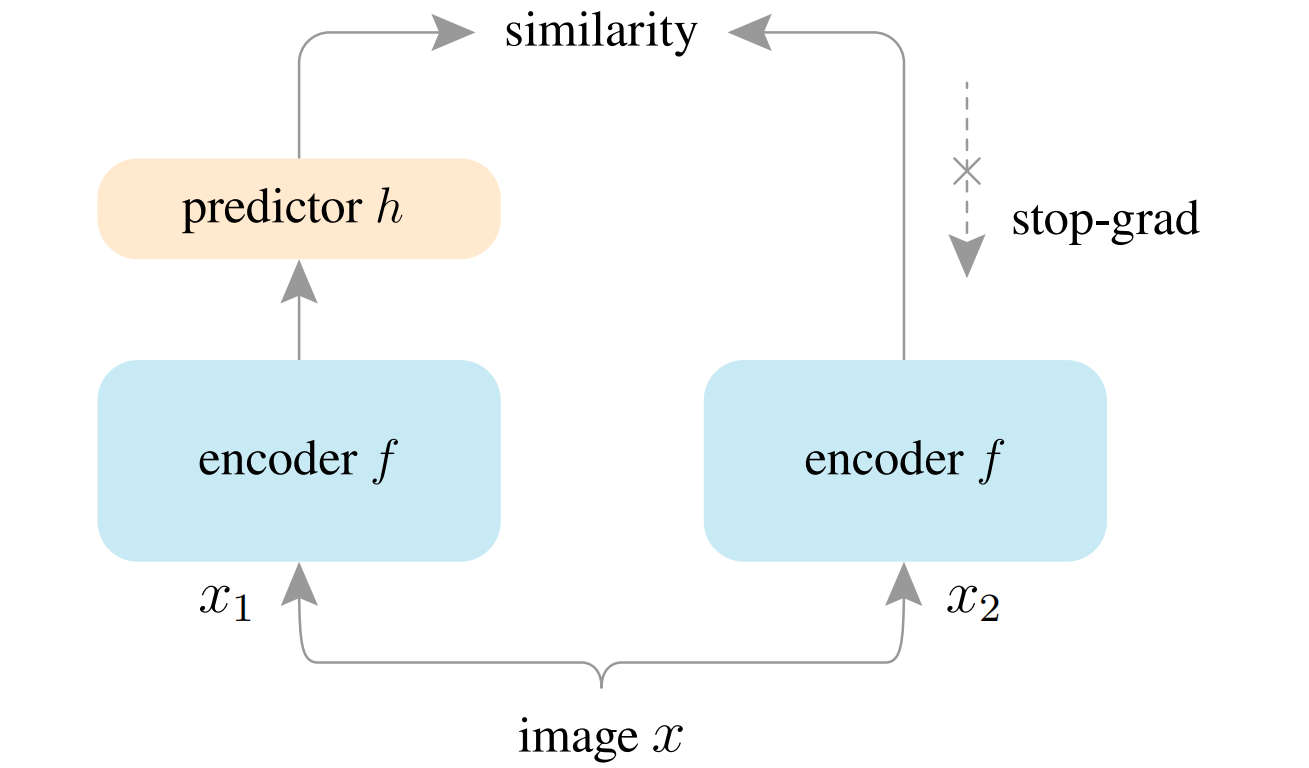
# f: backbone + projection mlp
# h: prediction mlp 
for x in loader: # load a minibatch x with n samples
    x1, x2 = aug(x), aug(x) # random augmentation对图像进行随机数据增强，这样就生成 
    z1, z2 = f(x1), f(x2) # projections, n-by-d encodeer的计算
    p1, p2 = h(z1), h(z2) # predictions, n-by-d predictor的计算
    L = D(p1, z2)/2 + D(p2, z1)/2 # loss  两个向量的负余弦相似度
    L.backward() # back-propagate
    update(f, h) # SGD update
def D(p, z): # negative cosine similarity
    z = z.detach() # stop gradient
    p = normalize(p, dim=1) # l2-normalize
    z = normalize(z, dim=1) # l2-normalize
    return -(p*z).sum(dim=1).mean()

在backward()时，如果y是标量，则不需要为backward()传入任何参数；否则，需要传入一个与y同形的Tensor。

如果不想要被继续追踪，可以调用.detach()将其从追踪记录中分离出来，这样就可以防止将来的计算被追踪，这样梯度就传不过去了。还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来，这种方法在评估模型的时候很常用，因为在评估模型时，我们并不需要计算可训练参数（requires_grad=True）的梯度。

上面将z给detach了，$\frac{z_2}{||z_2|{|}_2}$所以会被看成为常数只有$\frac{p_1}{||p_1|{|}_2}$会产生梯度，

为了进一步确认那一部分的设计在本文的框架中是至关重要的，作者设计了以下的消融实验。

---

Empirical Study

stop grad

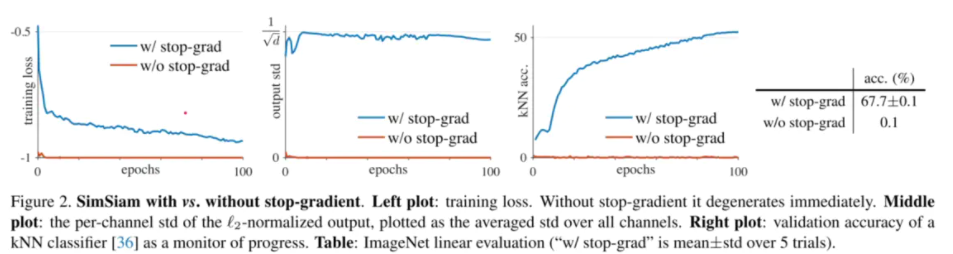
显然如果使两侧的梯度都进行传递网络的loss是非常小的，因为两个网络的参数是接近一模一样的所以两个网络很容易就达到一致了。而且这样的性能表现是非常差的，因为很容易达到两个网络参数一样，最后导致模型坍塌。实际上并不能学到什么有效的特征。

---

使用不同的predictor的结果

如果没有predictor模型不work（原因作者没说）；

如果预测MLP头模块h固定为随机初始化，该模型同样不再有效，这是因为模型不收敛，loss太高；

当预测MLP头模块采用常数学习率时，该模型甚至可以取得比基准更好的结果，作者也提出了一个可能的解释：h应当适应最新的表征，所以不需要在表征充分训练之前使用降低学习率的方法迫使其收敛。

不同Batch Size

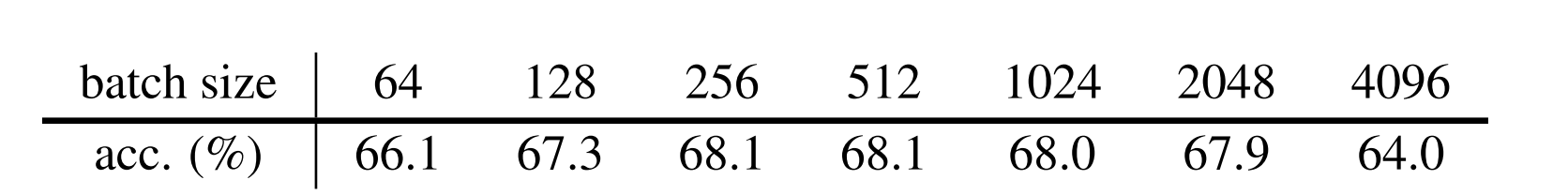
探究了不同的batch对精度的影响，虽然基础$lr$是0.05，但是学习率会随着batch的变化做线性缩放$lr\times BatchSize/256$ ，对于batch大于1024时，会采用10个epoch的warm-up学习率。

作者探究了SGD在较大batch上会导致性能退化，但同时也证明了优化器不是防止崩溃的必要条件。

---

Batch Normalization

移除BN之后可能因为难优化造成了性能下降，但是并没有造成collapsing，只加在隐层精度会提高到67.4%，如果在投影MLP中也加上BN则会提升到68.1%。但是如果把BN加到预测MLP上，就不work了，作者探究了这也不是崩溃问题，而是训练不稳定，loss震荡。

总结下来就是，BN在监督学习和非监督学习中都会使模型易于优化，但是并不能防止collapsing。

---

Similarity Function

除了余弦相似函数之外，该方法在交叉熵相似函数下也work，这里的softmax是channel维度的，softmax的输出可以认为是属于d个类别中每个类别的概率。

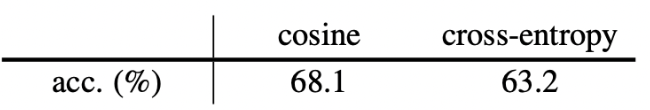
可以看出使用交叉熵相似性依然可以很好地收敛，并没有崩溃，所以避免collapsing与余弦相似性无关。

结果比较

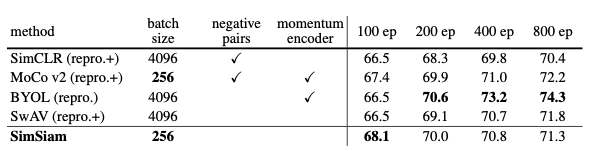
如下图7所示，SimSiam小的batch和没有负样本、momentum encoder的情况下仍然能取得较好的效果。

Hypothesis

为什么这样简单的网络能够work呢？作者提出了一种猜想：SimSiam实际上是一种Expectation-Maximization（EM）的算法。——最大期望算法。

我们最熟悉的最大期望算法就是k-means算法。

$$L(\theta ,\eta )={\mathbb{E}}_{x,\mathcal{T}}[\Vert {\mathcal{F}}_{\theta }(\mathcal{T}(x))-{\eta }_x{\Vert }_2^2]$$

这里x输入图像$\mathcal{T}$是图像的一种增强，${\mathcal{F}}_{\theta }$是encoder，${\eta }_x$不一定局限于图像表征，在训练网络时我们希望找到一个$\theta$，找到一个$\eta$，使得loss的期望是最小的。

在每一步中首先会确定一个$\theta$使得 loss 最小，这时使用的是一个固定的$\eta$，从而得到${\theta }^t$

${\theta }^t\leftarrow {\mathrm{argmin}}_{\theta }\mathcal{L}\theta {\eta }^{t-1}$（公式 2）

锁定$\theta$，寻找一个使 loss 达到最小的$\eta$

${\eta }^t\leftarrow {\mathrm{argmin}}_{\eta }\mathcal{L}({\theta }^t$))

反复进行以上两步最终使训练得到一个满意的结果。