1.齿轮

1.题目描述

这天, 小明在组装齿轮。

他一共有 $n$ 个齿轮, 第 $i$ 个齿轮的半径为 $r_i$, 他需要把这 $n$ 个齿轮按一定 顺序从左到右组装起来, 这样最左边的齿轮转起来之后, 可以传递到最右边的 齿轮, 并且这些齿轮能够起到提升或者降低转速 (角速度) 的作用。

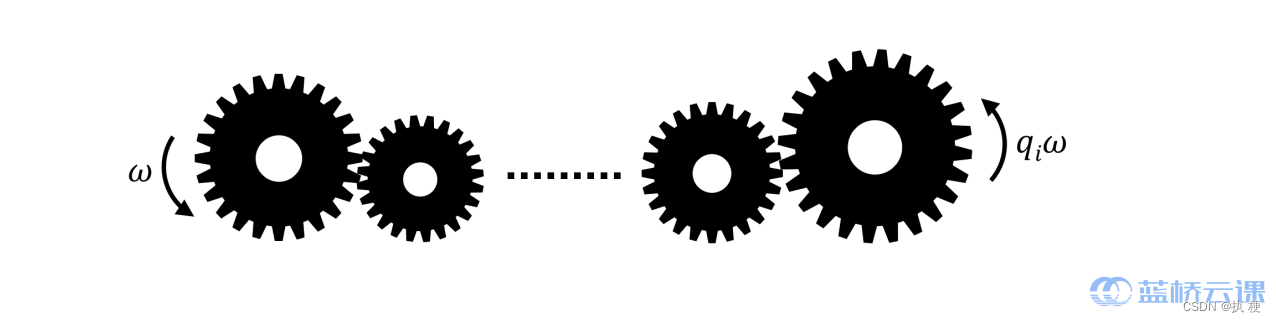
小明看着这些齿轮, 突然有 $Q$ 个疑问：能否按一定顺序组装这些齿轮使得 最右边的齿轮的转速是最左边的齿轮的 $q_i$ 倍?

2.输入格式

输入共 $Q+2$ 行, 第一行为两个正整数 $n,Q$, 表示齿轮数量和询问数量。
第二行为 $n$ 个正整数 $r_1,r_2,\dots ,r_n$, 表示每个齿轮的半径。后面 $Q$ 行, 每行一个正整数 $q_i$表示询问。

3.输出格式

$Q$ 行, 对于每个询问, 如果存在至少一种组装方案满足条件, 输出 ${{}^{\prime }\mathrm{YES}}^{\prime }$, 否则输出 ’ $\mathrm{NO}$ '。

4.样例输入

5 3
4 2 3 3 1
2
4
6

5.样例输出

YES
YES
NO

6.样例说明

询问 1 方案之一 ： 23341：23341
询问 2 方案之一：42331

询问 3 没有方案

6.数据范围

$n,Q\le 2\times 10^5;ri,qi\le 2\times 10^5$

7.原题链接

齿轮

2.解题思路

首先，这里涉及到一个物理公式，涉及到线速度$v,$角速度 $w$ 以及半径 $r$ 之间的关系。它们之间满足:
$$v=w\ast r$$

而齿轮模型是一个经典的物理模型，所有的齿轮的线速度都一样。 对于任意的齿轮之间都一定满足:
$$w_x\ast r_x=w_y\ast r_y$$

假设最左边的的齿轮半径为 $x$ ，最右边的齿轮半径为 $y$ ，那么使得最右边的齿轮的转速(角速度)是最左边的 $q$ 倍，则需满足：
$$w_x\ast q=w_y$$
联立上述两式可解得：
$$r_x=q\ast r_y$$

所以我们可知，我们只需要去判断所有齿轮的半径之间是否存在两个齿轮的半径是 $q$ 倍的关系。既然存在倍数关系，那么说明两个齿轮的半径其中一个必然是另外一个的因数。我们使用数组st，其中st[[i]表示是否有半径相差$q$倍的两个齿轮。

我们可以将齿轮半径按从小到大进行排序，对于每个齿轮的半径$r_i$，我们将去分解其所有的因数,如果存在某个数$x$是$r_i$的因数，并且之前已经出现过半径为$x$的齿轮，则说明当$q=r_i/x$时，我们是可以完成要求的。当然我们在分解因数时，应该进行优化，当$x$是$r_i$的因数时，$r_i/x$也一定是$r_i$的因数，此时我们可以直接一起进行判断。这样分解每个数的复杂度的$O(n)$级别降低到$O(\sqrt{n})$。

每次判断一个数后我们将其放入set中，在判断该数的因数在是否出现也是看set中是否存在。因为每个数的因数一定小于等于数的本身，所以这是我们排序的目的，确保了如果一个数的因数存在，那么一定会在它之前出现。

这个题目一定要注意一个点，齿轮的个数可能只有一个，那么此时左齿轮恰好就是右齿轮，如果查询的$q$为1时，是符合要求的，所以我们需要对这种情况进行特判。

时间复杂度：$O(n\sqrt{n})$

3.Ac_code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=200010;

bool st[N];
int r[N];
int main() 
{
	int n,q;
	scanf("%d%d",&n,&q);
	unordered_set<int> s;
	for(int i=0;i<n;++i){
		scanf("%d",&r[i]);
	}
	sort(r,r+n);
	for(int i=0;i<n;++i){
		int v=r[i];
		for(int i=1;i<=v/i;++i){
			if(v%i==0){
				//存在这个半径为i的齿轮
				if(s.find(i)!=s.end()){
					st[v/i]=true;
				}
				//存在这个半径为v/i的齿轮
				if(s.find(v/i)!=s.end()){
					st[i]=true;
				}
			}
		}
		s.insert(r[i]);
	}
	for(int i=0;i<q;++i){
		int h;
		scanf("%d",&h);
		if(n==1&&h==1) puts("YES");
		else if(st[h]) puts("YES");
		else puts("NO");
	}
    return 0;
}