逻辑回归原理

此前介绍的线性回归基本模型和增加了正则项的优化模型都只能用来预测连续值（标签值是多少），如果想要应用于分类问题（标签值是1还是0），就还需要进一步操作，即本文即将介绍的逻辑回归，其本质是预测标签值是1和0的概率分别为多少。

由于连续值的取值范围为$(-\infty ,+\infty )$，而概率值的取值范围是$(0,1)$，所以需要将线性回归模型得到的连续值做一次转换，压缩到$(0,1)$中。

sigmoid函数

在逻辑回归模型中，将连续值压缩的方式是使用sigmoid函数，其表达式为
$$f(x)=\frac{1}{1+e^{-x}}$$
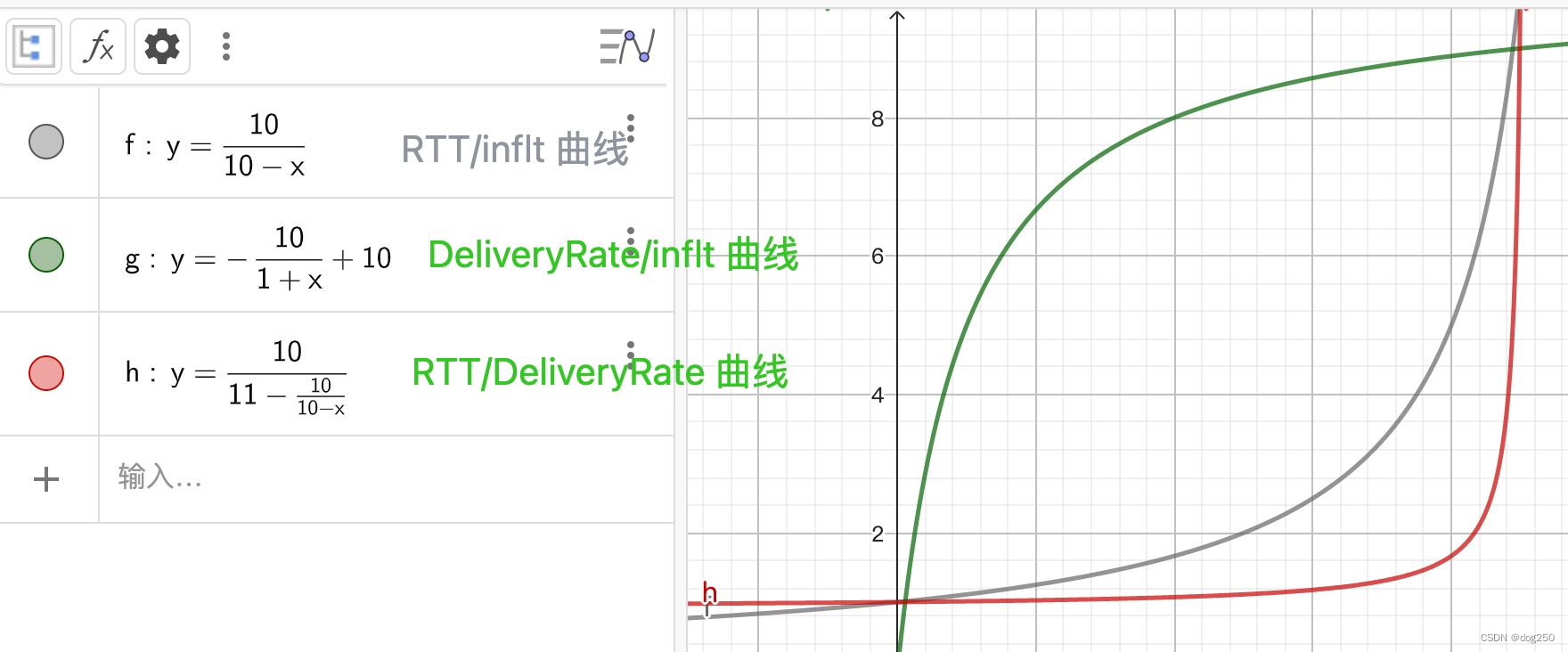
sigmoid函数的图形如下，显然$f(x)$的范围是$(0,1)$。

图形实线的Python代码为

import matplotlib.pyplot as plt
import numpy as np
import math


# sigmoid函数
def sigmoid(x):
    return 1 / (1 + math.exp(-x))
    

def plot_sigmoid():
    
    # 构造x和y数据
    x = np.linspace(-6, 6, 100)
    y = []
    for i in x:
        y.append(sigmoid(i))
    
    # 绘制基本数据
    plt.figure(figsize=(5, 5))
    plt.plot(x, y)
    
    # 将y轴移至坐标原点，并去除右侧实线
    ax = plt.gca()
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))
    ax.spines['right'].set_color('none')
    
    # 增加坐标标签
    plt.xlabel('x', loc='right')
    plt.ylabel('f(x)', loc='top', rotation=0)


if __name__ == '__main__':
    # 绘制sigmoid曲线
    plot_sigmoid()

除了以上的图示，我们还可以从数学角度来推演：针对样本的预测值$\hat{y}$，其线性回归表达式为
$$\hat{y}=w_1\ast x_1+w_2\ast x_2+...+w_n\ast x_n+b$$
$\hat{y}$的范围是$(-\infty ,+\infty )$，那么指数函数$e^{\hat{y}}$的范围是$(0,+\infty )$，构造如下的表达式
$$\frac{e^{\hat{y}}}{e^{\hat{y}}+1}$$
显然，上式的范围即为$(0,1)$，而对上式的分子和分母同时除以$e^{\hat{y}}$，得到
$$\frac{1}{1+e^{-\hat{y}}}$$
以上即为sigmoid函数。

到了这里，其实就出现了一个问题：逻辑回归为什么要使用sigmoid函数？是否可以使用其他函数替代？
我在网上找了很久，但并没有找到让我折服的解释，其中一篇算是说的比较全的了，放在这里以作参考。

优化建模

基于以上分析，我们可以做出以下定义：针对任意一个样本，其分类结果为1的概率为
$$f=\frac{1}{1+e^{-\hat{y}}}$$
其中，$\hat{y}=w_1\ast x_1+w_2\ast x_2+...+w_n\ast x_n+b$。

该样本被分类为0的概率即为
$$g=1-\frac{1}{1+e^{-\hat{y}}}$$
分子和分母同时乘以$e^{\hat{y}}$，得到
$$g=\frac{1}{1+e^{\hat{y}}}$$
对于该样本来说，要让分类模型准确，那么，如果真实标签$y$为1，则应该让$f$最大化；反之，应该让$g$最大化。
因此，对于整个训练集来说，可以建立优化模型为：寻找最佳的$w_1,w_2,...,w_n,b$，使得如下表达式最大化
$$F\ast G$$
其中，$F$为所有真实标签为1的样本对应的$f$函数的连乘；$G$为所有真实标签为0的样本对应的$g$函数的连乘。
事实上，此即为，概率论中的最大似然函数，不过名称不重要，重要的是对建模过程的理解。

以上定义的问题是一个无约束优化问题，可以使用很多优化算法求解，例如梯度类算法等。

代码实现

自编代码

接下来看一下，如何编写代码实现对权重系数$w$和截距$b$的优化计算。

以下代码中，使用的是forge数据集。该数据集有2维特征，所以待优化的变量有三个：$w_1,w_2,b$。values实现了对连乘的计算，同时在外侧增加了log函数，以此解决因为values本身数值过小而导致提前收敛的风险。优化方法使用的是scipy.optimize命令。

from scipy import optimize


# 自编代码，带优化函数
def f(t):

    # 【数据集1】forge
    X, y = forge()

    values = 0

    for i in range(len(y)):
        # 去log，否则数值太小，无法优化
        if y[i] == 1:
            values -= math.log(1 / (1 + math.exp(-t[0] * X[i, 0] - t[1] * X[i, 1] - t[2])))
        if y[i] == 0:
            values -= math.log(1 / (1 + math.exp(t[0] * X[i, 0] + t[1] * X[i, 1] + t[2])))

    return values


# self代码优化权重系数和截距
def logreg_by_self():

    res = optimize.minimize(f, [0, 0, 0], method='BFGS')
    print('coef_by_self: {}, intercept_by_self: {}'.format(res.x[0:2], res.x[2]))

sklearn代码

如果调用工具包，可以直接使用sklearn.linear_model中的LogisticRegression即可。

from sklearn.linear_model import LogisticRegression

# sklearn优化权重系数和截距
def logreg_by_sklearn():
    # 【数据集1】forge
    X, y = forge()

    logreg = LogisticRegression(penalty='none', solver="lbfgs")
    logreg.fit(X, y)
    print('coef_by_sklearn: {}, intercept_by_sklearn: {}'.format(logreg.coef_, logreg.intercept_))

代码测试

原理测试

首先校验自编代码的准确性，调用以上两个函数，对比各自得到的权重系数和截距值

if __name__ == '__main__':

    # 对比self和sklearn计算结果
    logreg_by_self()
    logreg_by_sklearn()

代码输出结果如下所示。显然，两个方法得到的权重系数和截距是一致的，由此验证了原理和代码的正确性。

coef_by_self: [1.28004377 4.13686808], intercept_by_self: -21.37174954243782
coef_by_sklearn: [[1.28004046 4.13685915]], intercept_by_sklearn: [-21.37170026]

交叉验证

事实上，逻辑回归模型中也可以使用交叉验证的策略，进一步提升算法的性能指标。以下代码针对cancer数据集，使用交叉验证的方式，得到了最佳的正则化系数C。

import numpy as np
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.model_selection import train_test_split


# sklearn代码实现逻辑回归
def logreg_cv_by_sklearn(X, y):
    # 数据集拆分
    X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

    # 构造不同的Cs值，logregCV交叉验证得到最佳C
    Cs = np.logspace(-5, 2, 20)
    # 默认solver是lbfgs，会提示未收敛，故修改为liblinear
    logregCV = LogisticRegressionCV(Cs=Cs, cv=5, solver="liblinear")
    logregCV.fit(X_train, y_train)
    print('Logreg_best_C: {}'.format(logregCV.C_))

    # 使用最佳C重新训练
    logreg = LogisticRegression(C=logregCV.C_[0], solver="liblinear")
    logreg.fit(X_train, y_train)

    print('Training set score: {}'.format(logreg.score(X_train, y_train)))
    print('Test set score: {}'.format(logreg.score(X_test, y_test)))


if __name__ == '__main__':

    # 【数据集3】cancer，用于实现交叉验证
    cancer_data, X_arr, y_arr = breast_cancer()
    # sklearn代码实现交叉验证
    logreg_cv_by_sklearn(X_arr, y_arr)

运行以上的程序，可以得到如下结果。

Logreg_best_C: [100.]
Training set score: 0.9741784037558685
Test set score: 0.965034965034965