Unity 算法之点集中计算绘制凸包的简单整理

一、简单介绍

二、Graham扫描法

第一种说明：

第二种说明：

三、代码（第二种说明）

四、参考文献

一、简单介绍

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

凸包（Convex Hull）是一个计算几何（图形学）中的概念。

在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。

X的凸包可以用X内所有点(X1，...Xn)的线性组合来构造.

在二维欧几里得空间中，凸包可想象为一条刚好包著所有点的橡皮圈。

用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点。

凸包：在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集被称为X的凸包。

给定一组离散的点，求得包围整个离散点的边的集合。
例如，在墙上随机定了N个钉子，然后用一个足够大的橡皮筋包围这些钉子，那么松开橡皮筋之后，橡皮筋的范围就是凸包。

那么凸包的算法，就是输入一组离散点，返回能够组成凸包的点，将这些点连接起来就是凸包了。
常用的凸包算法是Graham扫描法，和Jarvis步进法

二、Graham扫描法

时间复杂度：O(n㏒n)
思路：Graham扫描的思想是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，实际上就是进行极角排序，然后对其查询使用。

第一种说明：

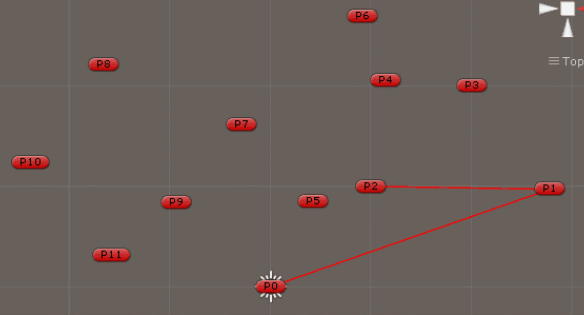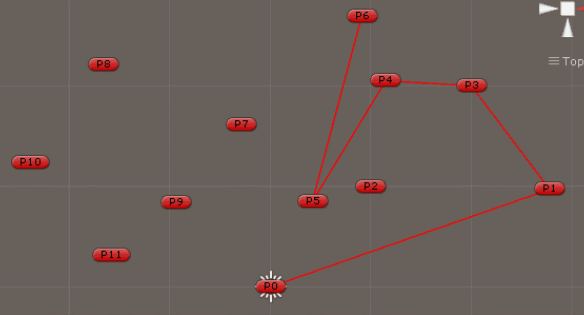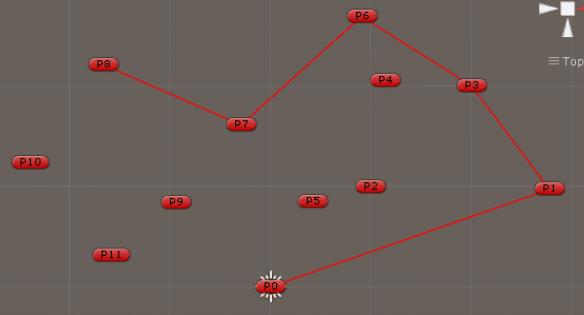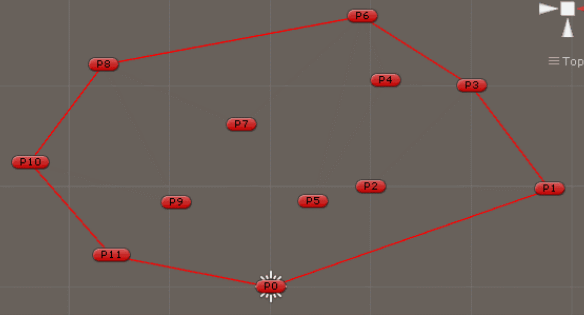
1、把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。

2、把所有点的坐标平移一下，使 P0 作为原点，如上图。

3、计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
（以上是准备步骤，以下开始求凸包）
以上，我们已经知道了凸包上的第一个点 P0 和第二个点 P1，我们把它们放在栈里面。现在从步骤3求得的那个结果里，把 P1 后面的那个点拿出来做当前点，即 P2 。接下来开始找第三个点：

4、连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。

5、如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。

6、当前点是凸包上的点，把它压入栈，执行步骤7。

7、检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。

第二种说明：

1、从离散点集合S中获取一个y轴最小，x轴最小的点 P0。（如果最小y轴有多个点，就取x轴最小的点）

2、计算S中其他的点到P0点的极角，并按照从小到大的顺序进行排序的到集合S1（极角相同，取距离最段的排在前），通过排序后可以确定PO点和排序后集合S1 中的第一个点P1点是凸包点，加入凸包列表中。

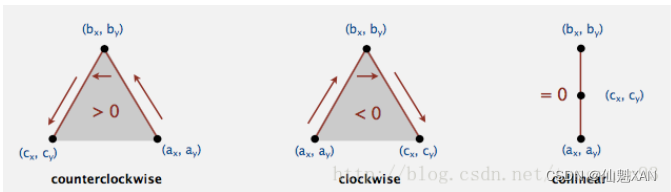
3、从S1中取得下一个点（P2），计算P2点位于线段（P0,01）的左边还是右边。

4、如果是左边，将P2点加入凸包点队列，如果右边，移除上一次加入的点（P1），重新计算P1点与集合中线段的位置关系（这里移除P1后，列表里只有一个，那就直接加入）

5、重复3到4步骤，知道S1中没有点为止。

三、代码（第二种说明）

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

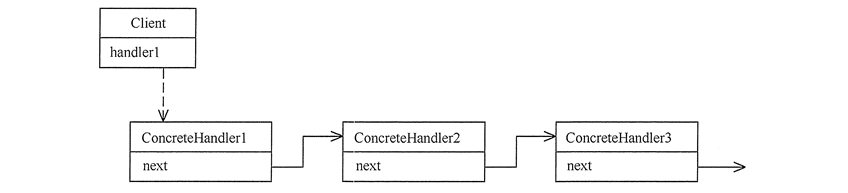
public class GrahamScan : MonoBehaviour {
    //离散的点
    public Transform[] Points;
    //组成边的顶点集合
    public List<Transform> ePoint = new List<Transform>();

    private bool IsFinsh = false;
    void Start()
    {
        Aritmetic();
    }

    //算法
    void Aritmetic()
    {
        Transform bp = BasePoint();
        bp.name = "P0";
        ePoint.Add(bp);
        Transform[] polarSort = PolarSort(bp);
        for (int i = 0; i < polarSort.Length; i++)
        {
            if (polarSort[i] == bp) continue;
            polarSort[i].name = "P" + (i + 1);
        }
        //通过排序，而可以得知 第一个点肯定在凸边上
        ePoint.Add(polarSort[0]);
        StartCoroutine(Ia(polarSort));
    }

    IEnumerator Ia(Transform[] polarSort)
    {
        for (int i = 1; i < polarSort.Length; i++)
        {
            yield return new WaitForSeconds(1);
            ePoint.Add(polarSort[i]);
            float d = PointDir(ePoint[ePoint.Count-1].position, ePoint[ePoint.Count - 2].position, ePoint[ePoint.Count - 3].position);
            if (d <= 0)
                continue;
            while (true)
            {
                yield return new WaitForSeconds(1);
                ePoint.RemoveAt(ePoint.Count-2);
                d = PointDir(ePoint[ePoint.Count - 1].position, ePoint[ePoint.Count - 2].position, ePoint[ePoint.Count - 3].position);
                if (d < 0)
                    break;
            }
        }
        IsFinsh = true;
    }

    void OnDrawGizmos()
    {
        Gizmos.color = Color.red;
        if (!IsFinsh)
        {
            for (int i = 0; i < ePoint.Count - 1; i++)
                Gizmos.DrawLine(ePoint[i].position, ePoint[i + 1].position);
            return;
        }

        for (int i = 0; i < ePoint.Count; i++)
        {
            if (i == ePoint.Count - 1)
            {
                Gizmos.DrawLine(ePoint[i].position,ePoint[0].position);
                continue;
            }
            Gizmos.DrawLine(ePoint[i].position,ePoint[i+1].position);
        }

    }

    /// <summary>
    /// 获取基点P0
    /// </summary>
    /// <returns></returns>
    Transform BasePoint()
    {
        //取y值最小 如果多个y值相等，去x最小(这里y 我们取z)
        Transform minPoint = Points[0];
        for (int i = 1; i < Points.Length; i++)
        {
            if (Points[i].position.z < minPoint.position.z)
                minPoint = Points[i];
            else if (Points[i].position.z < minPoint.position.z)
                minPoint = Points[i].position.x < minPoint.position.x ? Points[i] : minPoint;
        }
        return minPoint;
    }
    /// <summary>
    /// 获取点的方向 =0 在线上 <0在左侧 >0在右侧
    /// </summary>
    /// <param name="p"></param>
    /// <param name="p1"></param>
    /// <param name="p2"></param>
    /// <returns></returns>
    float PointDir(Vector3 p, Vector3 p1, Vector3 p2)
    {
        Vector3 v1 = p1 - p;
        Vector3 v2 = p2 - p1;
        float f = v1.x * v2.z - v2.x * v1.z;
        return f;
    }

    /// <summary>
    /// 极角排序
    /// </summary>
    /// <param name="bp"></param>
    /// <returns></returns>
    Transform[] PolarSort(Transform bp)
    {
        List<Transform> p = new List<Transform>();
        for (int i = 0; i < Points.Length; i++)
        {
            //如果是自己，则跳过
            if (Points[i] == bp) continue;
            Vector3 v = Vector3.zero;
            float e = GetProlar(Points[i], bp,out v);
            int index = -1;
            for (int j = 0; j < p.Count; j++)
            {
                Vector3 v1 = Vector3.zero;
                float e1 = GetProlar(p[j],bp,out v1);
                if (e1 > e)
                {
                    index = j;
                    break;
                }
                if (e1 == e && v.magnitude < v1.magnitude)
                {
                    index = j;
                    break;
                }
            }
            if (index == -1)
            {
                p.Add(Points[i]);
                continue;
            }
            p.Insert(index,Points[i]);
        }
        return p.ToArray();
    }
    /// <summary>
    /// 获取极角
    /// </summary>
    /// <param name="pos1"></param>
    /// <param name="pos2"></param>
    /// <returns></returns>
    float GetProlar(Transform pos1, Transform pos2,out Vector3 v)
    {
        v = pos1.position - pos2.position;
        return Mathf.Atan2(v.z,v.x);
    }

}