牛客练习赛106
C
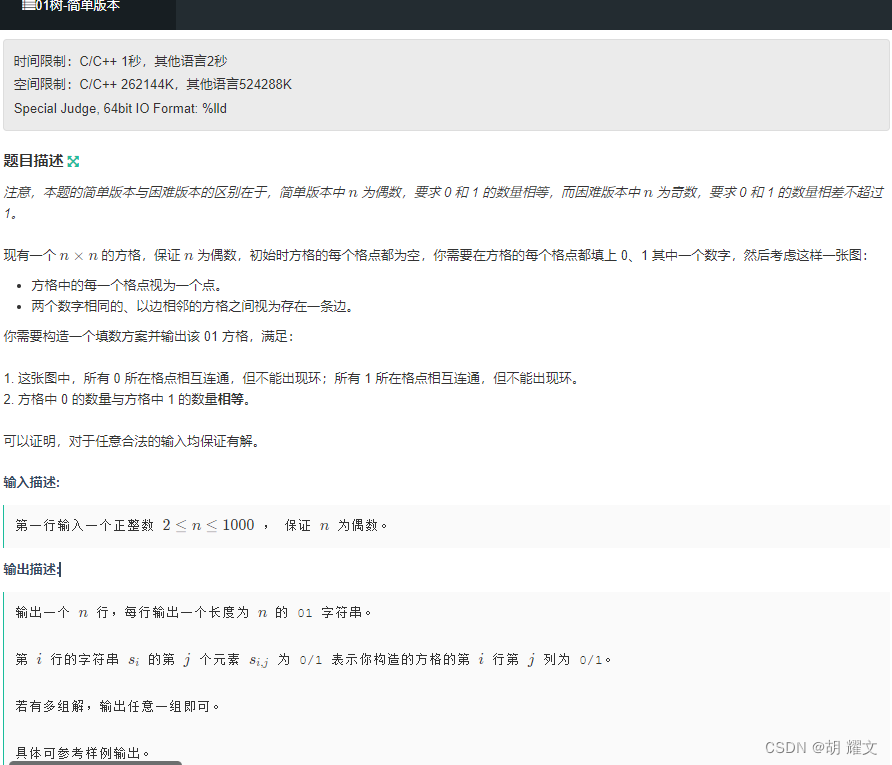
D
脑筋急转弯的构造题
E
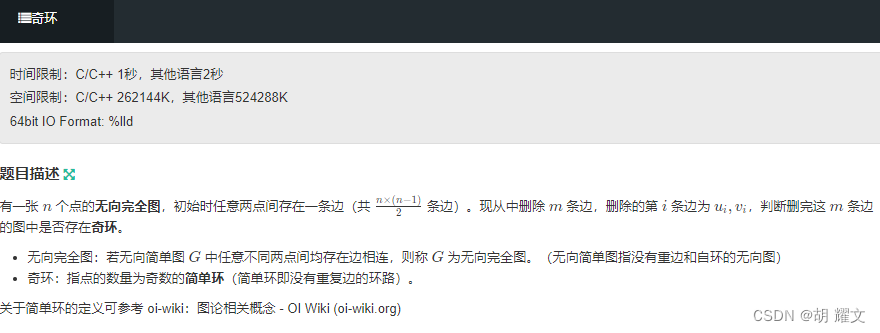
染色法判断二分图
结论,这个图是二分图说明不存在奇环
设左边是x,右边是y
则有
x
+
y
=
n
,
x+y=n,
x+y=n,且
x
∗
y
>
=
边
数
=
n
∗
(
n
−
1
)
/
2
−
m
x*y>=边数=n*(n-1)/2-m
x∗y>=边数=n∗(n−1)/2−m
也就是说左式最大是
n
∗
n
/
4
(
x
=
n
/
2
,
y
=
n
/
2
)
n*n/4 (x=n/2,y=n/2)
n∗n/4(x=n/2,y=n/2)
带
入
m
最
大
是
2
e
5
得
到
n
<
=
896
带入m最大是2e5得到n<=896
带入m最大是2e5得到n<=896
当n大于896或者最大交集数小于边数的话直接可以判断不是二分图
当n小于896时可以O(n+m)染色法判断是否是二分图
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10,M=2*N;
int T,n,m;
int a[1010][1010],c[1010];
int vis[1010];
int dfs(int u,int c=1){
vis[u]=c;
for(int i=1;i<=n;i++){
if(a[i][u]||i==u)continue;
if(vis[i]&&vis[i]!=3-c)return 0;
if(vis[i]==0&&!dfs(i,3-c))return 0;
}
return 1;
}
signed main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>T;
while(T--){
cin>>n>>m;
if(n<896)memset(a,0,sizeof a);
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
if(n<896)a[x][y]=a[y][x]=1;
}
if(n*n/4-n/2>m || n>=896){cout<<"YES"<<'\n';continue;}
memset(vis,0,sizeof vis);
// cout<<"ans="<<dfs(1)<<'\n';
int ok=1;
for(int i=1;i<=n;i++){
if(!vis[i]){
ok&=dfs(i);
if(ok==0)break;
}
}
if(ok)cout<<"NO"<<'\n';
else cout<<"YES"<<'\n';
}
}
F
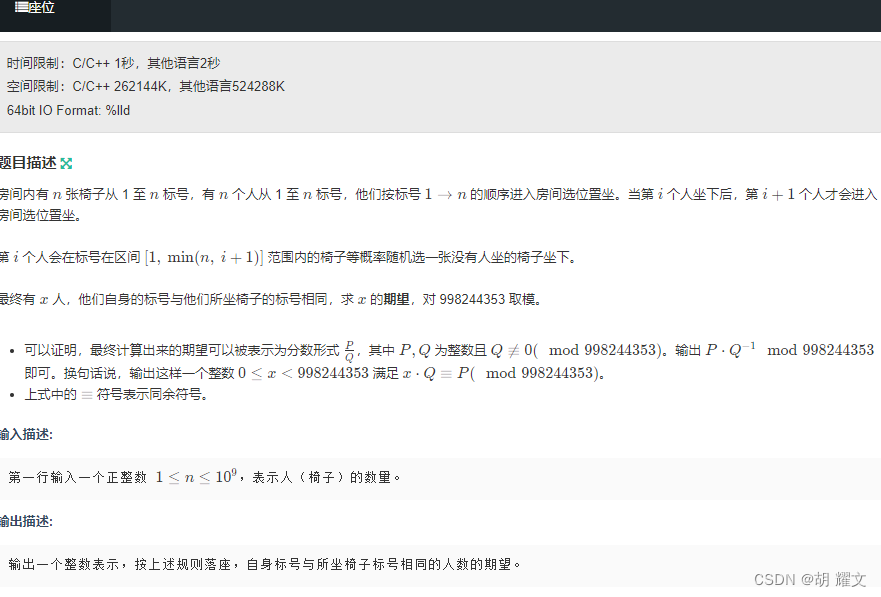
考虑每个人对答案的贡献,
第一个人坐对位置的概率是1/2
第n个人做对位置的概率取决于前面那个人是否坐错位置概率是1/2
其他人坐对位置概率是(前面人坐错)且(自己坐对)答案是1/4
所以答案是n<=2时是1,其他是1/2+(n-2)/4+1/2=(n+2)/4
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
int n;
int qpow(int a,int b){
int ans=1;
while(b){
if(b&1)ans=ans*a%mod;
b/=2;
a=a*a%mod;
}
return ans;
}
signed main(){
cin>>n;
if(n<=2)cout<<1;
else cout<<(n+2)*qpow(4,mod-2)%mod;
}
G
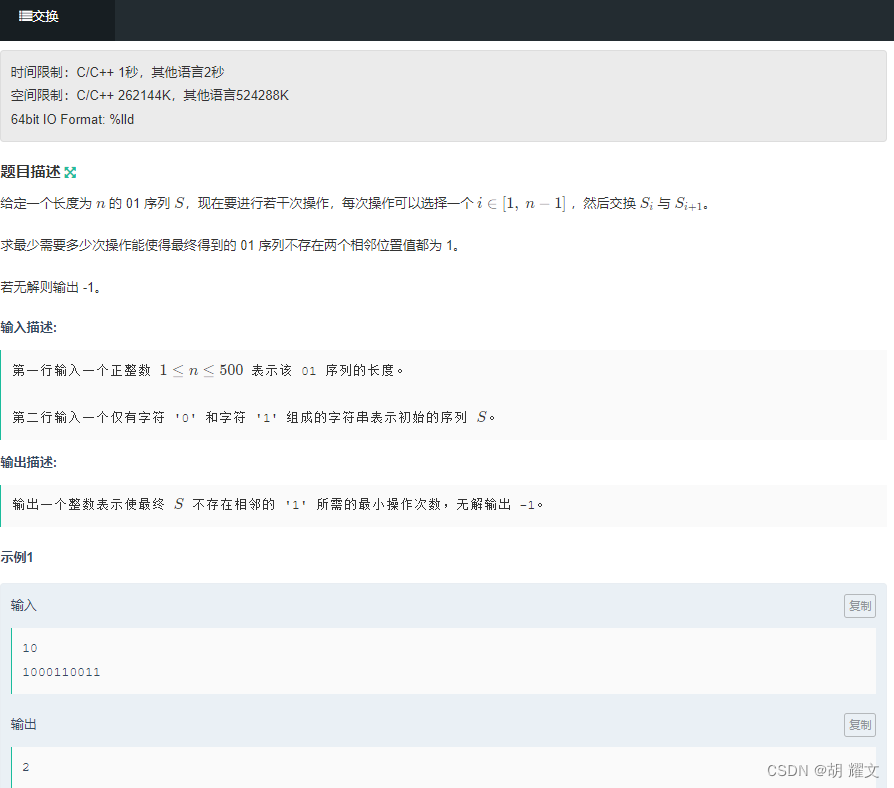
很好的一道题
解法1 dp
时间复杂度是 O ( n 2 ) O(n^2) O(n2)
设
d
p
[
i
]
[
j
]
[
0
/
1
]
dp[i][j][0/1]
dp[i][j][0/1]表示前i个位置塞了j个1,第i个位置是不是1,的最小代价
那么,初始化dp[0][0][0]=0
考虑第i个位置,塞j个1的状态
d
p
[
i
]
[
j
]
[
0
]
=
m
i
n
(
d
p
[
i
−
1
]
[
j
]
[
0
]
,
d
p
[
i
−
1
]
[
j
]
[
1
]
)
dp[i][j][0]=min(dp[i-1][j][0],dp[i-1][j][1])
dp[i][j][0]=min(dp[i−1][j][0],dp[i−1][j][1])
d
p
[
i
]
[
j
]
[
1
]
=
d
p
[
i
−
1
]
[
j
−
1
]
[
0
]
+
a
b
s
(
i
−
p
[
j
]
)
dp[i][j][1]=dp[i-1][j-1][0]+abs(i-p[j])
dp[i][j][1]=dp[i−1][j−1][0]+abs(i−p[j])
p[j]表示第j的1的位置
其实也就是让这个字符串里的1重排
#include<bits/stdc++.h>
using namespace std;
const int N=505;
int p[N],n,a[N],f[N][N][2];
signed main(){
ios::sync_with_stdio(0);cin.tie(0);
cin>>n;
int cnt=0;
for(int i=1;i<=n;i++){
char c;
cin>>c;
a[i]=c-'0';
if(a[i]==1)p[++cnt]=i;
}
memset(f,0x3f,sizeof f);
f[0][0][0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=i;j++){
if(j==0)f[i][j][0]=f[i-1][j][0];
else{
f[i][j][0]=min(f[i-1][j][0],f[i-1][j][1]);
f[i][j][1]=f[i-1][j-1][0]+abs(i-p[j]);
}
}
}
int ans=min(f[n][cnt][0],f[n][cnt][1]);
if(ans==0x3f3f3f3f)ans=-1;
cout<<ans;
}
解法2费用流
把1看作容器壁,把0看作水

那么题意就是要求移动水使得每个容器至少都有水
S
−
−
流
量
=
水
量
费
用
=
0
−
−
>
容
器
S--^{费用=0}_{流量=水量}-->容器
S−−流量=水量费用=0−−>容器
容
器
−
−
流
量
=
1
费
用
=
0
−
−
>
T
容器--^{费用=0}_{流量=1}-->T
容器−−流量=1费用=0−−>T
容 器 i 向 i − 1 , i + 1 连 边 , 容 量 是 I N F , 费 用 是 1 容器i向i-1,i+1连边,容量是INF,费用是1 容器i向i−1,i+1连边,容量是INF,费用是1
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=1e6+10;
int n,m,S,T,h[N],e[M],ne[M],f[M],w[M];
int incf[N],pre[N],d[N],st[N],idx,q[N];
void add(int a,int b,int c,int d){
e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++;
e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++;
}
bool spfa(){
memset(d,0x3f,sizeof d);
memset(incf,0,sizeof incf);
int hh=0,tt=1;
q[0]=S,d[S]=0,incf[S]=1e9;
while(hh!=tt){
int t=q[hh++];
if(hh==N)hh=0;
st[t]=0;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]&&d[ver]>d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
st[ver]=1;
q[tt++]=ver;
if(tt==N)tt=0;
}
}
}
}
return incf[T]>0;
}
void EK(int &flow,int &cost){
flow=cost=0;
while(spfa()){
int t=incf[T];
flow+=t;
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
memset(h,-1,sizeof h);
// cin>>n>>m>>S>>T;
string s;
int len;
cin>>len>>s;
S=0,T=N-1;
cin>>len>>s;
int sum=0,id=0,cnt=0;
for(int i=0;i<len;i++){
int x=s[i]-'0';
sum+=(x==0);
if(x==1){
cnt++;
id++;
// cout<<"id="<<id<<" sum="<<sum<<'\n';
add(S,id,sum,0);
sum=0;
}
}
id++;
// cout<<"id="<<id<<" sum="<<sum<<'\n';
add(S,id,sum,0);
for(int i=2;i<id;i++)add(i,T,1,0);
if(cnt>(len+1)/2){
cout<<-1;
return 0;
}
if(cnt==1){
cout<<0;
return 0;
}
for(int i=1;i<=id;i++){
if(i==1)add(i,i+1,1e9,1);
else if(i==id)add(i,i-1,1e9,1);
else add(i,i-1,1e9,1),add(i,i+1,1e9,1);
}
int flow,cost;
EK(flow,cost);
cout<<cost;
}

![[附源码]计算机毕业设计ssm校园一卡通服务平台](https://img-blog.csdnimg.cn/1d06ef2aaec34ead9a32094a73251654.png)
![[附源码]计算机毕业设计基于springboot的家政服务平台](https://img-blog.csdnimg.cn/c1fa8b8299ca48b5a20f70d97283853e.png)

![[附源码]Python计算机毕业设计Django框架的食品安全监督平台的设计与实现](https://img-blog.csdnimg.cn/d6d8f5deaf264b9b9145e19c411e9877.png)




![[附源码]计算机毕业设计毕业生就业管理系统](https://img-blog.csdnimg.cn/03d58f0760ff4b0197b13439a3e6cfdf.png)


