机器人控制算法八之路径规划算法：RRT、RRT-Connect、Dynamic-Domain RRTs*

本文主要介绍基于RRT快速搜索随机树的路径规划算法及其改进，主要参考以下论文：

• 1.1998 Rapidly-exploring random trees: A new tool for path planning
• 2.IEEE2000 RRT-connect: An efficient approach to single-query path planning
• 3.Adaptive tuning of the sampling domain for dynamic-domain RRTs

1.快速搜索随机树：RRT

1.1 摘要

  我们引入了快速搜索随机树(RRT)的概念，作为一种随机数据结构，它被设计用于广泛的路径规划问题。尽管它们拥有现有随机规划技术的许多有益特性，但RRTs是专门设计来处理非完整约束(包括动力学)和高自由度的。RRT是通过应用控制输入来迭代扩展的，这些控制输入将系统略微推向随机选择的点，而不是像概率路线图方法那样要求点对点收敛。讨论了rrt的几个理想属性和一个基本实现。到目前为止，我们已经成功地将RRTs应用于完整、非完整和运动学规划问题，最多可达12个自由度。

• 在过去的十年中，已经提出了几种随机化方法，并成功地应用于高维构型空间中的路径规划问题。比较流行的两种方法包括随机化势场算法和概率路线图算法。

  • 随机势场法在很大程度上依赖于选择一个好的启发式势函数，当遇到障碍、运动学微分约束和动力学约束时，这就成为一项艰巨的任务。在概率路线图方法中，通过生成随机配置并尝试将相邻的配置对与a连接，在配置空间中构造一个图将连接对配置的本地计划器。对于完整系统或可操纵的非完整系统的规划，局部规划步骤可能是有效的;然而，一般来说，连接问题可能与设计非线性控制器一样困难，特别是对于复杂的非完整和动态系统。
  • 概率路线图技术可能需要成千上万个构型或状态的连接来找到一个解决方案，如果每个连接都类似于一个非线性控制问题，它似乎不现实的许多非完整(和运动学)问题出现在机器人和相关的区域。

• 在本文中，我们引入了一种用于路径规划的随机数据结构，该结构设计用于具有非完整约束的问题。这导致了快速探索随机树(RRT)的引入，它在第2节中定义。RRT包含一些与概率路线图相同的理想属性。这两种设计都带有较少的启发式和随意性参数尽可能多。这往往会导致更好的性能分析和行为的一致性。它还促进了方法对相关应用程序的适应。RRTs的独特优势是可以直接应用于非完整和运动学规划。这种优势源于这样一个事实，即rrt不需要在对配置(或状态)之间建立任何连接，而概率路线图通常需要成千上万个连接。如前所述，对于完整路径规划来说，rrt可能比基本的概率路线图更有效。

1.2 RRT

快速搜索随机树：Rapidly-Exploring Random Trees

• 路径规划通常被视为在度量空间X中搜索从初始状态T到目标区域X 或目标状态E的连续路径。

  • 1.首先，给定目标及其初始状态、终点状态对应位置
  • 2.在场景中随机生成一个采样点，起点指向采样点的方向即为随机树枝干生长方向，在起点与采样点之间进行插值
  • 3.如果新增的路径中：起点与插值点的连线没有与障碍物发生碰撞（碰撞检测），则将插值点添加到树的结构中，并将点坐标作为路径信息保存至一条路径
  • 4.继续步骤2，3 ，如果插值点与终点相同时，则终止算法
    

• 将二维场景中的随机树搜索过程总结如下图所示：
  

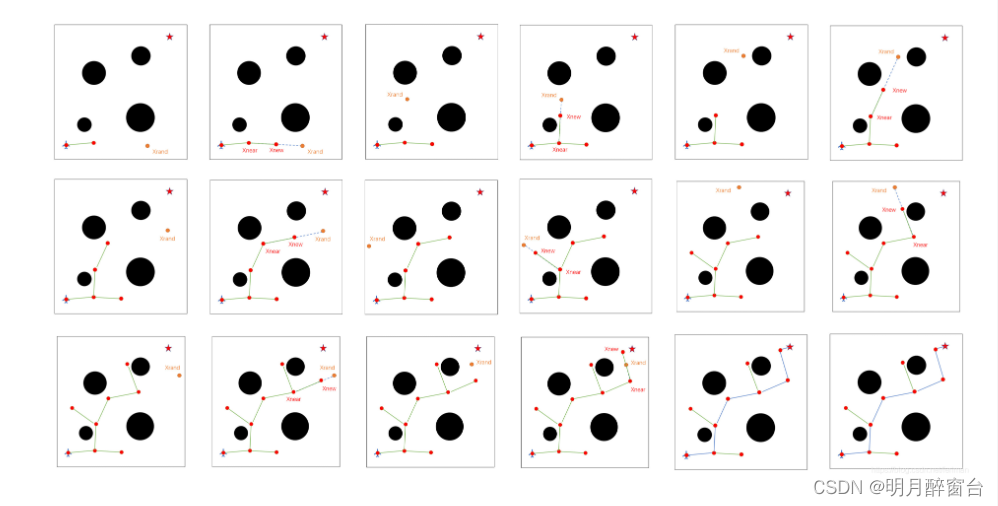
1.3 RRTs的优势

本节介绍了rrt的几个特性，这些特性使它们非常适合于各种各样的实际规划问题。RRT的主要优点是:

• 1. RRT的扩展严重偏向于状态空间的未开发部分;
• 2. RRT中的顶点分布接近抽样分布，导致行为一致;
• 3. RRT在非常一般的条件下是概率完整的;
• 4. RRT算法相对简单，便于性能分析(这也是概率路线图的首选特性);
• 5. RRT总是保持连接，即使边的数量是最小的;
• 6. 可再生交通可被认为是一个路径规划模块，它可以被改编和整合到各种规划系统中;
• 7. 整个路径规划算法可以在不需要在两个规定状态之间操纵系统的情况下构建，这极大地拓宽了RRTs的适用性。

1.4 RRT实例

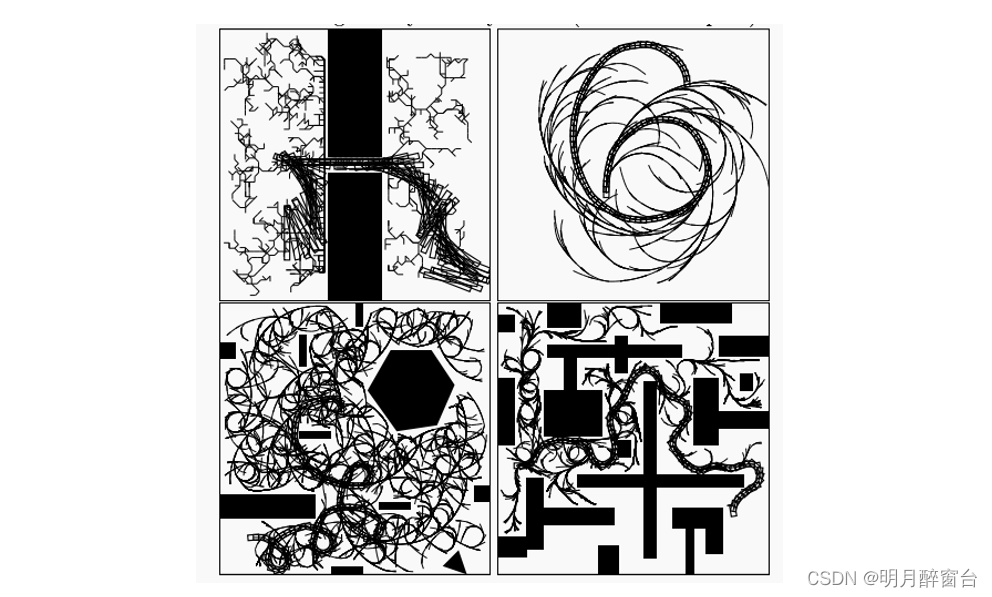
上面的每个例子都显示了在二维环境中运动的二维刚体。显示了RRT到平面的投影，以及机器人的计算路径。在左上角，一个紧约束的三维完整规划问题的解决方案显示。右上方显示的是只允许向前移动和不同程度右转的汽车的RRT。左下显示了在杂乱环境中不可控汽车的计算解。这辆车只能在三个不同的增量中向前移动和向左转弯(它甚至不能直线移动)。图1显示了汽车5自由度动力学模型的RRT和计算轨迹。上图右下部分显示了在杂乱环境中相同模型的解决方案路径。目前的实施忽略了许多效率问题;然而，到目前为止，计算性能是令人鼓舞的。

2. RRT-Connect

RRT-Connect：一种有效的单查询路径规划方法

2.1 摘要

  提出了一种简单而有效的求解高维配置空间单查询路径规划问题的随机算法。该方法的工作原理是逐步构建两个快速探索的随机树（RRTs）。这些树都探索周围的空间，并通过使用简单的贪婪启发式向彼此推进。虽然该算法最初设计为计划人体手臂的运动（建模为7-DOF运动链），用于无碰撞抓取和操作任务的自动图形动画，但该算法已成功应用于各种路径规划问题。计算示例包括在2D和3D工作空间中为刚性物体生成无碰撞运动，以及在3D工作空间中为6-DOF的PUMA臂生成的无碰撞操作运动。并进行了一些基本的理论分析。

• 随机路径规划算法通常是针对两种上下文之一而设计的：单查询规划和多查询规划。对于单查询规划，假设单路径规划问题必须快速解决，而不需要进行任何预处理。解决这一问题的最早和最流行的方法之一是随机视场方法。对于多查询规划，假设在相同的环境下可以解决许多路径规划问题。在这种情况下，值得对信息进行预处理，并将其存储在允许快速路径规划查询的数据结构中。概率路线图方法是第一个解决这个问题的方法。通过随机选择许多配置，并使用本地规划器来连接附近的配置对，在配置空间中构造一个图。
• 由于其简单性和可靠的行为，概率路线图方法近年来取得了相当大的成功，目前的研究主要集中在分析和病理病例的治疗。即使对于随机潜在现场规划器可能产生更好的性能的单查询问题，概率路线图方法由于其可靠性而受到青睐。随机势场规划器通常通过在配置空间上以势函数的形式编码贪婪启发式来找到单个查询问题的快速解决方案。当计划者陷入局部最小值时，随机游走被用来尝试逃跑；然而，很难确保可靠性能。
• 这自然导致了对一种简单、可靠的方法的探索，该方法具有概率路线图的许多伟大特性，但是专门为单查询路径规划设计的。我们提出了一种简单的路径规划方法，称为RRT-连接，它结合了快速探索的随机树（RRTs）和一个简单的贪婪启发式，该启发式积极地尝试连接两棵树，一棵来自初始配置，另一棵来自目标。从初始和目标配置构造搜索树的想法来自于经典的人工智能双向搜索。我们的想法的关键是使用rrt作为一个简单的采样方案和数据结构，从而可靠地导致对配置空间的快速和统一的探索。RRT-Connect最初是为7-DOF人体手臂规划无碰撞运动，用于交互式3D虚拟环境[中动画角色的抓取和操作任务的自动动画，然而，它也被发现是对各种路径规划问题的高效和可靠的。

2.2 快速搜索随机树

再谈RRT：作为一种有效的数据结构和采样方案，可以快速搜索具有代数约束（障碍）和微分约束（非整体和动力学）的高维空间。关键的思想是使探索偏向于空间中未被探索的部分。

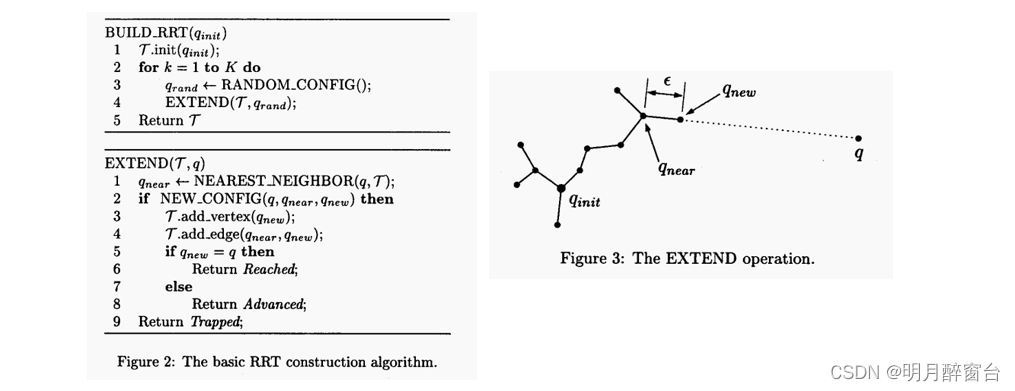
  基本的RRT构造算法如图2所示。每个步骤中执行的一个简单迭代，都试图通过添加一个由随机选择的配置有偏差的新顶点来扩展RRT。扩展函数，如图3所示，选择RRT中已经到给定样本配置最近的顶点q。函数NEW-CONFIG以一些固定的增量距离向 q 移动 $ϵ$，并测试碰撞。这可以使用增量距离计算算法快速执行（“几乎恒定的时间”）。可以发生三种情况：

• 到达，q直接添加到RRT，因为它已经包含在距离 $ϵ$ 中的一个顶点；
• 高级，一个新顶点q_new != q 被添加到RRT；
• 捕获，其中提出的新顶点被拒绝，因为它不在Cjree中。

图4的顶部一行显示了一个在二维正方形空间中构建的RRT。

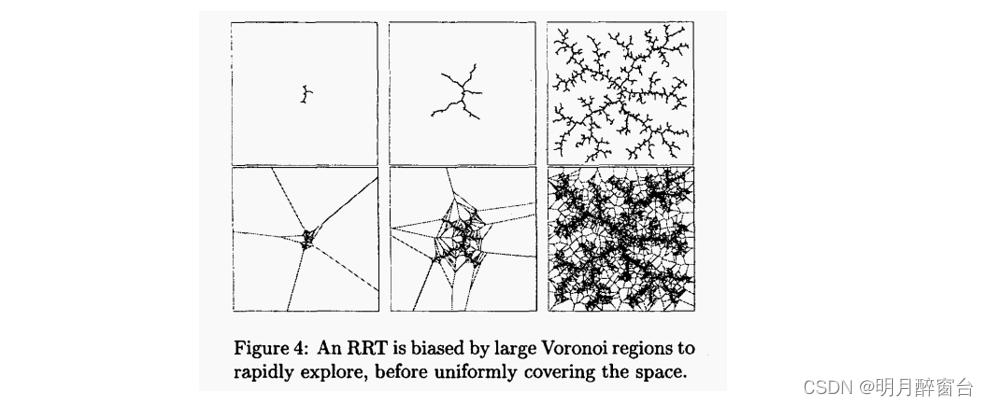
2.3 RRT-Connect 路径规划器

• RRT-连接规划器是专门为不涉及微分约束的路径规划问题而设计的。在这种情况下，对增量运动的需要就不那么重要了。该方法基于两个想法：连接启发式，试图移动到更长的距离，和RRTs的增长：由起点到终点。
• 连接启发式是一个贪婪函数，可以被认为是图2中的扩展函数的替代方案。连接启发式不是尝试通过一个E步来扩展RRT，而是迭代扩展步骤，直到达到q或一个障碍。（扩展：先随机生成一点，然后插值后判断路径有无碰撞，循环往复；迭代：以一个设定的步进朝一个方向不断迭代，直至发生碰撞则改变方向，可以看作扩展的结果极速版）
  
• 图5显示了RRT-连接-规划器算法，它可以与图2中的构建算法进行比较。两棵树，a和b一直保持，直到它们连接并找到解决方案。
  

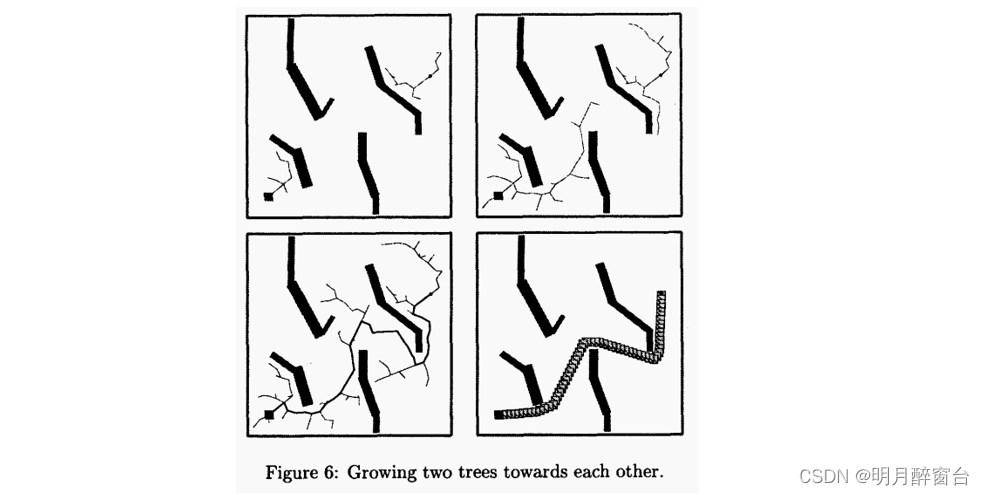
2.4 实验结果

  进行了各种更具挑战性的实验。图8描述了一架三角钢琴（超过4500个三角形）从一个房间在墙壁和低障碍物中从一个房间移动到另一个房间的三维模型的计算解决方案。为了解决这个查询，钢琴需要进行几个棘手的旋转。平均计算时间为12.5秒（100次试验）。
  对一个6-DOF Puma工业机械臂模型进行了操纵规划实验。结合逆运动学算法，RRTConnect规划器通过计算高级运动请求的三个运动，促进了任务级控制机制来规划操作运动： 1)移动手臂以抓住物体；2)将物体移动到目标位置；3)释放物体，将手臂返回到静止位置。图9显示了将书籍从中间书架移动到桌子底部书架的路径的几个快照。其中3个查询平均在4秒内得到解决。

3.动态域 RRTs* 的采样域的自适应调整

Adaptive Tuning of the Sampling Domain for Dynamic-Domain RRTs∗ ：动态域RRTs∗的采样域的自适应调整

3.1 摘要

  最近，一种名为动态域RRT的新规划器已经被开发出来的[28]，它在许多运动规划问题上显著优于其他现有的基于RRT的规划器。规划器的抽样方案考虑了配置空间的障碍，使其沃罗诺伊偏差。这有助于显著减少为了找到解决方案路径所需的迭代次数。因此，对于复杂的几何图形问题，可以更快地解决一个数量级。
  最初，动态域rrt被提出有一个额外的参数，它对应于采样域的大小。该算法的性能依赖于对每个特定的运动规划问题对该参数的仔细调整，这使得该方法与原始的rrt相比更难使用。在本文中，我们提出了一个改进版本的动态域RRT，它可以自动调整输入参数，从而产生更鲁棒的性能。我们在各种经典的运动规划问题上评估了所提出的方法。

3.2 RRT框架

• RRTs的探索是由树中节点的Voronoi（多边形）图决定的。选择一个节点进行扩展的概率与其沃罗诺伊区域的体积成正比。因此，rrt倾向于在构型空间的未探索区域快速增长。注意，该算法的固有特性不需要显式的Voronoi图的计算。

• 依赖于提前配置空间边界，采样域是由构型空间的边界来定义的。由于规划器的行为依赖于边界节点的Voronoi区域，因此它也取决于这些边界的特定设置。如果这些边界的选择不适合于一个给定的运动规划问题，那么规划器的效率就会受到极大的影响。

  • 传统上，在扩展开始时，当配置空间的体积明显大于树所覆盖的区域时，边界节点对配置空间中未被探索的部分提供了特别强的偏差。这通常有助于树木的快速生长。然而，当一个边界节点也是一个边界节点时，即当它靠近障碍物时，这可能会导致性能减慢。这样的节点有很高的概率被选择向障碍物的方向进行扩展，但大多数情况下扩展失败。
    
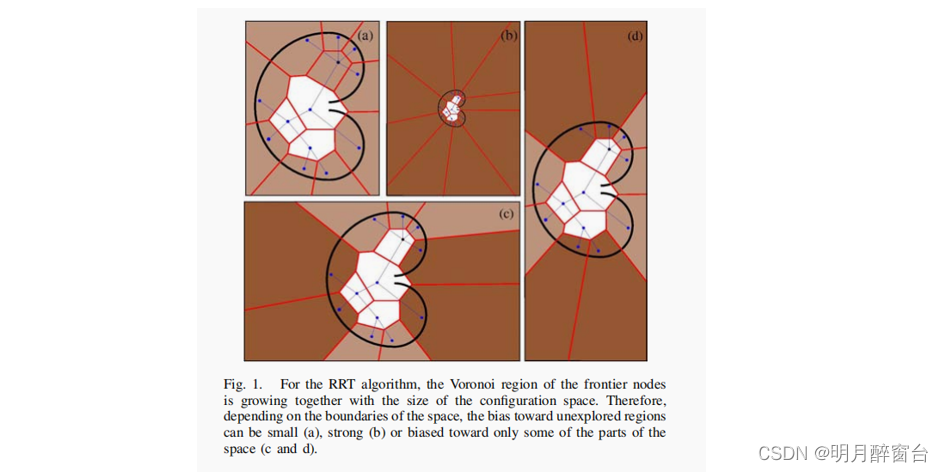
  • 图1中的示例说明了这个问题。任务是将机器人移到一个有虫子陷阱的障碍物之外。由于通道狭窄，这个问题对任何运动规划者来说都是一个挑战。对于经典的RRT算法，困难也来自于边界节点迅速成为边界节点。因此，规划器的性能在很大程度上取决于如何设置环境的边界。在图1 (a)中，环境的边界接近于树的覆盖范围。因此，它为细化勘探区域内的现有树，从而解决问题提供了一个很好的机会。在(b)中，采样域远远大于树的大小。在这种情况下，它将导致许多无用的尝试扩展的边界节点向障碍。甚至，它会降低规划器的性能。
  • 示例 c 和(d)说明了另一种情况，导致只对配置空间的某些方向的任意偏差。为了克服这一缺点，DDRRT算法提出了一种控制树中节点的Voronoi偏差的方法，并打破了这种对环境边界的隐式依赖性。

3.3 动态域RRT路径规划器

• 虽然在这些可见的Voronoi区域上的均匀分布（图2 b）可以理想地规避经典rrt的偏差问题（图2 a），但它的计算是一个非常困难的问题。因此提出了另一种分布，它保留了可见性分布的良好特性，但计算效率更高（图2 c）。
  

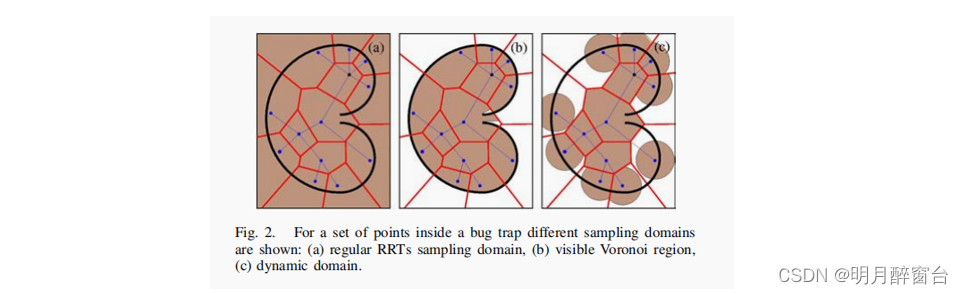
• 边界节点v的可见Voronoi区域近似于其边界域，该边界域定义为v的Voronoi区域与以v为中心的n维球的交点。那么一组点的半径R的动态域是边界点与所有其他点的Voronoi区域相结合的边界域。在这个域上的均匀分布称为动态域分布。

  • 为了获得动态域分布，首先从构型空间生成一个分布，然后限制在动态域内。由于原始分布是均匀的，所得到的限制也是均匀的。计算这个动态分布对应于图3的算法描述中的第3-6行。如果每个点的半径是一个边界点，则每个点的半径设置为值R，否则设置为值∞。注意，为了使这一步有效，可以从非常接近动态域的区域中选择随机构型。实际上，这意味着我们在包含所有边界域的最小边界框内进行采样。
    
  • DD-RRT算法的伪代码如图3所示。该算法会动态地更新有关边界点的信息。在探索树的开始时，所有的点都被认为是非边界的。一旦给定节点的扩展失败，它就变成一个边界节点。这对应于代码中的第11- 12行。然后将该节点的半径场更新为R。在接下来的迭代中，来自该节点的Voronoi区域的样本被限制在其边界域内。让我们注意到，由于边界节点的偏差减少，树倾向于在自由空间中产生更多的节点。此外，在找到属于动态域的样本之前，许多样本可能会被拒绝。因此，应采用适用于配置空间拓扑结构的有效最近邻方法。

• 动态域半径的影响

  • 我们可以为基于RRT的规划器区分两种主要的扩展模式混合在一起。第一种是一种探索模式，它引导树向配置空间的未探索区域扩展。这种探索模式是通过扩展边界节点来实现的。第二种模式对应于由于在树已经覆盖的区域中添加新节点而产生的细化模式。
  • 动态域半径R的值应该被仔细选择，因为它控制了这两种膨胀模式之间的平衡。半径越大，探索效果就越强，这也会损害树的细化。
  • 在实践中，这意味着一个过小或过重要的半径会降低规划器的性能（参见图4）。这种行为已经在不同的例子上得到了实验验证（见图7、8 和图9）。一般来说，当半径的值设置在“最优”半径值的一半到两倍之间时，我们可以说性能仍然接近于最佳值。在这些界限之外，性能迅速下降，半径从“最优”值越远，性能就越差。
    
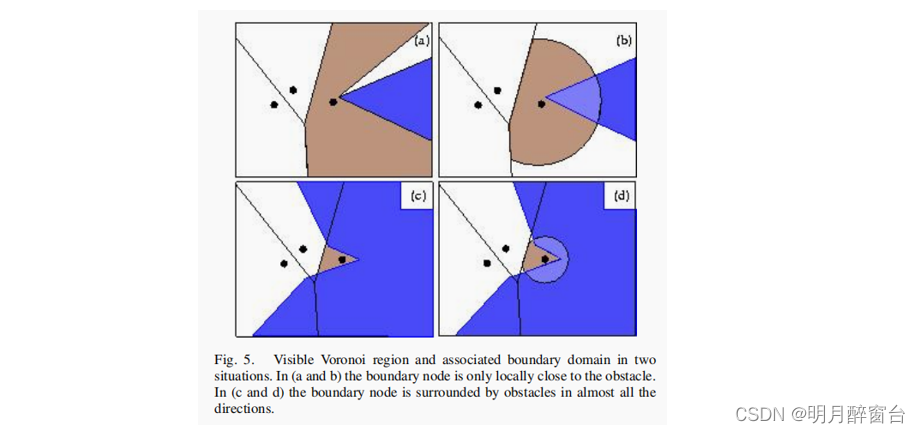
  • 在初始的DD-RRT算法中，每个点的半径只能有两个值：如果是边界点，值R，否则值∞。这两个值之间没有转换。正如我们之前所解释的，我们希望边界域尽可能地适应该点的可见Voronoi区域，但这个域非常不同，这取决于它是否被障碍强烈包围（见图5）。然而，只要该节点被定义为一个边界节点，则其边界域总是由相同的给定半径来定义。
    

• 下面，我们建议在搜索过程中独立地调整每个节点的半径。这种适应有两个主要优势。首先，它可以帮助自动平衡分配给探索和细化的权重。其次，它允许局部区分规划者的行为，从而更好地使其适应自由空间的形状。

3.4 采样域的自适应调整

• 图5的示例说明了一个边界节点的两种情况，其中蓝色表示障碍物。在第一个（a和b）中，尽管靠近障碍物，节点的可见Voronoi区域在a中仍然是一个较大的区域，与b中一个具有较大半径值的边界域相比更加友好。在第二种情况下（c和d），节点被障碍物强烈包围，因此其可见的Voronoi区域©是很小的，而d中具有一个小半径值的边界域更适合于这种情况。
• 这一观察结果意味着，在扩展节点的各种尝试过程中获得的信息可以帮助更好地评估节点周围的可见Voronoi域。每次一个给定节点的扩展失败时，该节点被障碍强烈包围的概率就会增加。每一次成功，这种概率就会降低。因此，我们建议将给定节点的边界域（即其相关的半径）作为该节点的扩展尝试次数和失败次数的函数。
• 表示包含自适应半径修改的DD-RRT算法的伪代码如图6所示。一旦其中一个节点的扩展失败，该节点就成为边界节点。然后将其半径初始化为一个给定的值。然后，每次选择节点进行扩展时，将根据扩展尝试的成功或失败情况修改其关联半径。如果尝试成功，然后导致在树中创建一个新的节点，那么半径值将增加一个给定的百分比α（算法的第10行）。相反，如果展开失败，半径值将降低相同的比例（算法的第17行）。
  
• 为了保持算法的概率完备性，我们始终确保一个节点被扩展的可能性。为此，我们给节点的可能半径值设置了一个下界（在图6的算法中没有显示）。这个边界是当我们尝试展开一个节点时，用于检查冲突的插值步骤的倍数。
• 最后一点是为α定义一个值。在实验中，我们注意到这个参数的值根本不像半径参数在DD-RRT的初始版本中那样重要。α的一个小值（通常是几个百分点）就足以增加算法的鲁棒性，并将在下一节的实验中使用。

3.5 实验结果

这里不具体写了，放一些效果吧，如有需求可以详见论文：

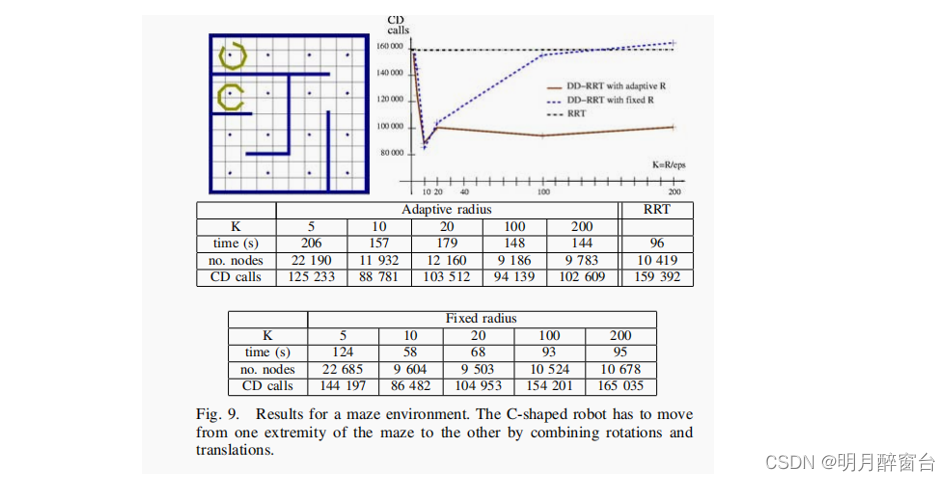
• DD-RRT算法是一种特别有效的算法，对于复杂的几何问题的碰撞测试是昂贵的。在本文中，我们提出了一种新的动态域RRT算法的扩展。该扩展通过在搜索过程中自动调整每个节点的影响区域，显著提高了规划器的鲁棒性。改进DD-RRT算法还有其他几个研究方向。
• 特别是，关于到障碍物的距离的信息可以用来定义动态域。
• 另一个重要的方向是研究DD-RRT框架在其他约束运动规划问题上的应用，如闭链杆规划或微分约束下的规划，其中迭代计算的成本和Voronoi偏差都极大地影响了规划算法的效率。