A. Twin Permutations

A. Twin Permutations

1、分析

作者这里的构造方法是让最终的数组满足：$a_1+b_1=a_2+b_2=...=a_i+b_i=n+1$

现在来证明一下这个构造方法的正确性。

因为我们的和是确定的，所以$b_i=n+1-a_i$
由于我们的$a_i$是一个排列，所以$a_i$是两两不同的，因此$b_i$也是两两不同的。因为$a$的范围是$[1,n]$，所以$b$的范围是$[1,n]$。而$b$数组的长度又是$n$。因此，$b$数组是一个从$1$到$n$的两两不同的长度为$n$的数列，即$b$数组是一个排列。符合题意。

2、代码

#include<bits/stdc++.h>
using namespace std;

void solve()
{
	int n;
	cin >> n;
	vector<int>a(n);
	for(auto &x : a)
		cin >> x;
		
	for(int i = 0; i < n; i ++)
	{
		cout << n - a[i] + 1 << " ";
	}
	cout << endl;
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	int t;
	cin >> t;
	while(t--)
	solve();
}

B. Array merging

B. Array merging

1、分析

这道题有一个很重要的性质，即每次只取两个数组的第一个元素的其中一个。如果没有这个性质的话，直接数一数两个数组中不同数字出现的次数和，输出最大值即可。那么这个性质的存在，又对答案产生了什么影响呢？

这里证明两件事情：

第一件事情：任意两段连续相同数字可以拼接在一起。
假设我们想要将A和B拼在一起，只需要先将A和B前面的数字都取出来，拼接在前面，再取A和B即可。

第二件事情：任意三段及以上的连续相同数字无法拼接在一起。

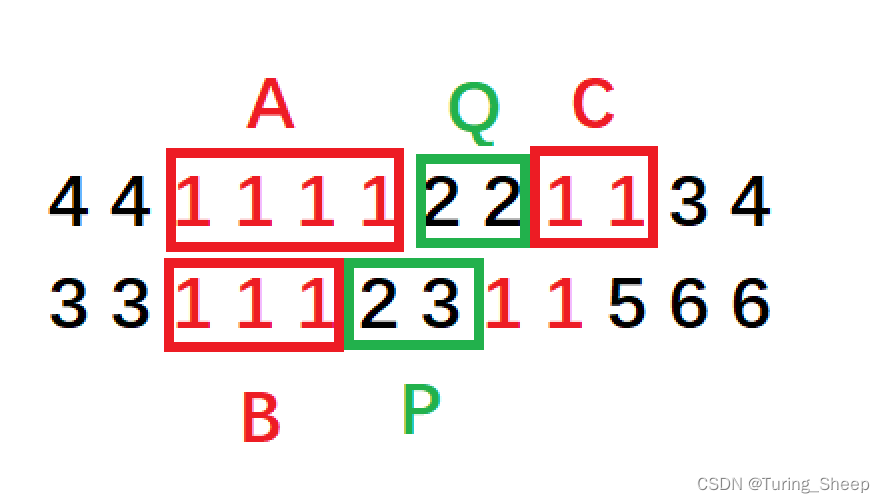
如上图所示，假设我们想要将ABC三段连接在一起，当我们将A和B连接在一起后，后面就必须接上Q和P中间的数字，也就是说我们A和B组成的连续数字必定被打断，所以C是无法接到A+B的后面的。

通过上面的两个证明，我们可以得到以下结论：
对于任意数字，在两个数组中分别求出最长连续相同数字的个数，再相加。
这样对于任何数字，都能得到一个相加后的数字。再从这些数字里取出一个最大值即可。

#include<bits/stdc++.h>
using namespace std;

void solve()
{
	int n;
	cin >> n;
	vector<int>a(n), b(n);
	for(int i = 0; i < n; i ++)
		cin >> a[i];
	for(int i = 0; i < n; i ++)
		cin >> b[i];
	
	map<int,int>ca, cb;
	for(int i = 0; i < n; i ++)
	{
		int cnt = 1;
		while(i + 1 < n && a[i] == a[i + 1])
			cnt ++, i ++;
		ca[a[i]] = max(ca[a[i]], cnt);
	}
	for(int i = 0; i < n; i ++)
	{
		int cnt = 1;
		while(i + 1 < n && b[i] == b[i + 1])
			cnt ++, i ++;
		cb[b[i]] = max(cb[b[i]], cnt);
	}
	map<int,int>ans;

	for(auto x : ca)
		ans[x.first] += x.second;	

	for(auto x : cb)
		ans[x.first] += x.second;

	int ANS = 0;
	for(auto x : ans)
		ANS = max(x.second, ANS);
	cout << ANS << endl;
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	int t;
	cin >> t;
	while(t--)
	solve();
}

2、代码

C. Copil Copac Draws Trees

C. Copil Copac Draws Trees

1、分析

对于树的问题，我们可以先考虑一条链的情况。

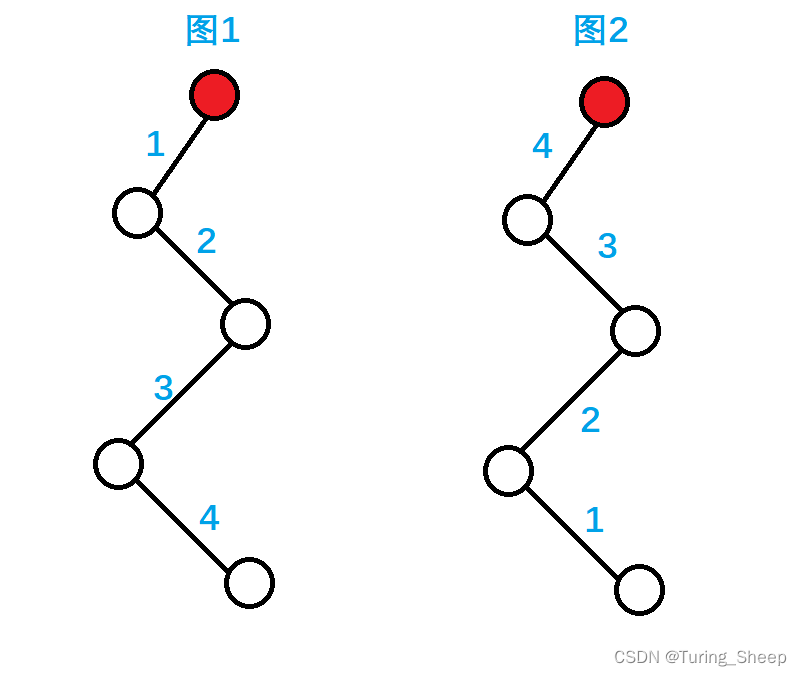
边上 所标的数字是该边在输入的时候的顺序。根据题意，左图可以依次从上到下涂色，即只需要一次操作。而右图则是一个很极端的情况，右图需要4次操作。

那么有什么规律呢？

我们可以发现下面的规律：

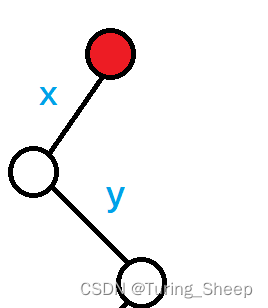
如果$x<y$则在一次操作中，可以将两个点涂色。若$x>y$，则在一次操作中，无法同时将两个点操作。这里的$x>y$可以看作一个逆序对。

对于一条链而言，操作的次数等于该链上的逆序对个数+1。

接着我们再考虑一棵树的情况。

一棵树可以看做很多条链。

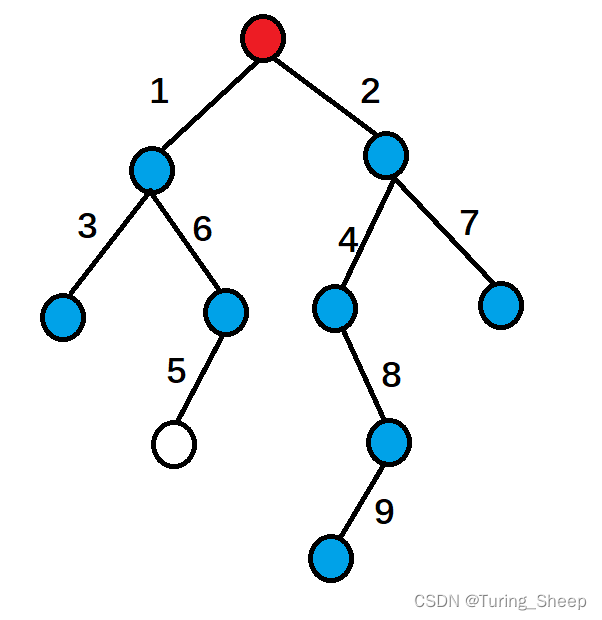
在第一次操作的过程中，图中的蓝色的点会被成功的涂色。 在第二次操作中，白色的点会被成功涂色。那么最终的答案就是2。我们将这棵树看成各种链，便可以得到下面的情况。

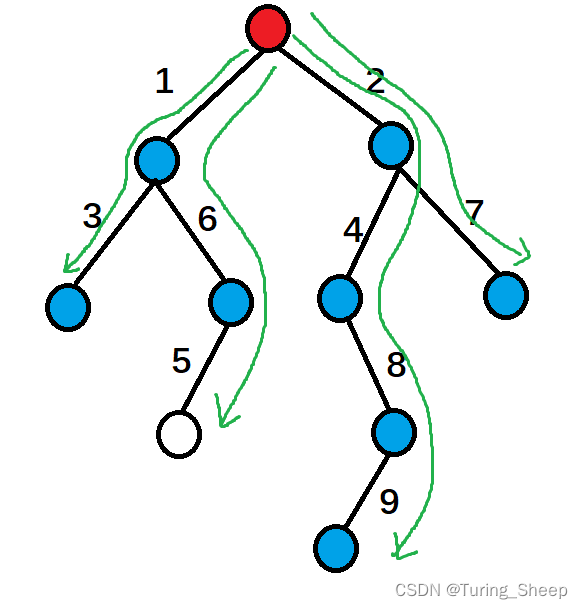
拆成图中的4条链后，我们就可以利用刚刚的结论，得到每一条链的操作次数。而我们发现，这棵树的答案就是这些链操作次数的最大值。

因此，我们只需要在DFS的过程中，求出每条链的操作次数，再取一个最大值输出即可。

2、代码

#include<bits/stdc++.h>
#define endl '\n'
#define x first
#define y second
using namespace std;
typedef pair<int,int> pii;
const int N = 2e5 + 10;
int e[N], f[N];
vector<pii>edge[N];
int ans = 0;

void dfs(int u, int father)
{
	for(auto [a, b]: edge[u])
	{
		if(a == father)
			continue;
		e[a] = b;
		f[a] = f[u] + (b < e[u]);
		dfs(a, u);
	}	
}

void solve()
{
	int n;
	cin >> n;
	for(int i = 0; i < n - 1; i ++)
	{
		int a, b;
		cin >> a >> b;
		edge[a].push_back({b, i});
		edge[b].push_back({a, i});
	}
	dfs(1, -1);
	int maxv = 0;
	for(int i = 0; i <= n; i ++)
	{
		maxv = max(f[i], maxv);
	}
	cout << maxv + 1 << endl;

	for(int i = 0; i <= n; i ++)
		edge[i].clear();
	for(int i = 0; i <= n; i ++)
		e[i] = f[i] = 0;
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	int t;
	cin >> t;
	while(t--)
	solve();
}

D. The BOSS Can Count Pairs

D. The BOSS Can Count Pairs

1、分析

我们先思考暴力做法，最暴力的做法就是去枚举所有可能的数对，然后再判断这个数对是否满足$a_i\ast a_j=b_i+b_j$。这个过程可以写作$C_n^2=\frac{n(n-1)}{2}$，即时间复杂度是$O(n^2)$的。很明显这个做法超时了。

接下来我们想一想如何优化暴力算法。

我们发现这道题有一个很关键的性质：$a_i\le n$ 和 $b_i⪇n$。

这就说明我们的$b_i+b_j⪇2n$，即 $a_i\ast a_j\le 2n$。

即 $min(a_i,a_j)⪇\sqrt{2n}$

那么我们可以去枚举$min(a_i,a_j)$。（不妨将这个最小值记作$s$，这个$s$当作$a_j$）。

然后我们再去枚举数对$(a_i,b_i)$。接着我们就可以利用式子：$a_i\ast a_j=b_i+b_j$计算出$b_j$。

即$b_j=a_i\ast a_j-b_i=s\ast a_i-b_i$。

那么我们的$(a_j,b_j)$即$(s,s\ast a_i-b_i)$，而这个数对的个数就是该数对对答案的贡献。

现在我们有两个问题需要解决。

由于我们枚举的是$min(a_i,a_j)$，所以我们需要保证$a_i\ge s$的。

如果不这样保证，会出现重复的问题。

同时，为了计算贡献，我们需要开一个数组记录所有$(s,b_i)$的个数。

如果$a_i>s$就按照刚刚的推导计算即可。

如果$a_i=s$的话，这里需要去重。

为什么要去重？

因为此时的$a_i=s$，所以此时我们选择的两个数对是：$(s,b_i)$和$(s,b_j)$。按照刚刚的思路，我们的$(i,j)$和$(j,i)$都会被计算进来。实则这两个算一种。

2、代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define a first
#define b second
using namespace std;
const int N = 1e5 + 10;

void solve()
{
	int n, ans = 0;
	cin >> n;
	vector<pair<int,int>>c(n);
	for(int i = 0; i < n; i ++)
		cin >> c[i].a;
	for(int i = 0; i < n; i ++)
		cin >> c[i].b;
	vector<int>cnt(n + 1);
	for(int s = 1; s * s <= 2 * n; s ++)
	{
		cnt.assign(n + 1, 0);
		for(int i = 0; i < n; i ++)
			if(c[i].a == s)
				cnt[c[i].b] ++;
		int cc = 0;
		for(int i = 0; i < n; i ++)
		{
			if(c[i].a < s)
				continue;
			int x = s * c[i].a - c[i].b;
			if(x < 1 || x > n)
				continue;
			if(c[i].a == s)
				cc += (cnt[x] - (c[i].b == x));
			else
				ans += cnt[x];
		}
		ans += (cc / 2);
	}
	cout << ans << endl;
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	int t;
	cin >> t;
	while(t--)
	solve();
}