摘要: 主成分分析 (principal component analysis, PCA) 是一种有理论依据的无监督特征提取的线性方法.
1. 特征选择与特征提取
- 特征选择是指从已有的特征里面选择出一个子集. 例如: 身高、体重、性别、年龄、体温、血相等等, 如果要一个人是否患流感,身高、体重等不但没有作用, 反而还会让分类器效果变差. 回头想想 k k kNN, 在计算距离时考虑一些不相关的特征, 会使得相似的样本变得不相似.
- 特征提取则是指从已有特征中生成新的特征. 例如: 人们常说自己有多重, 然后表达想减肥的意愿. 但这种想法是错误的, 应该从计算 BMI, 以此确定自己是否偏胖. 这里 “从计算 BMI”, 就是一个特征提取的过程.
总的来说, 特征选择相对简单, 而特征提取有很大的相像空间. 后面将会介绍的神经网络, 其最本质的任务就是特征提取.
2. PCA 的基本思想
PCA 有两个特点:
- 进行无监督的特征提取, 即它不考虑标签;
- 是一个线性模型, 即新特征均为原始特征的线性组合.
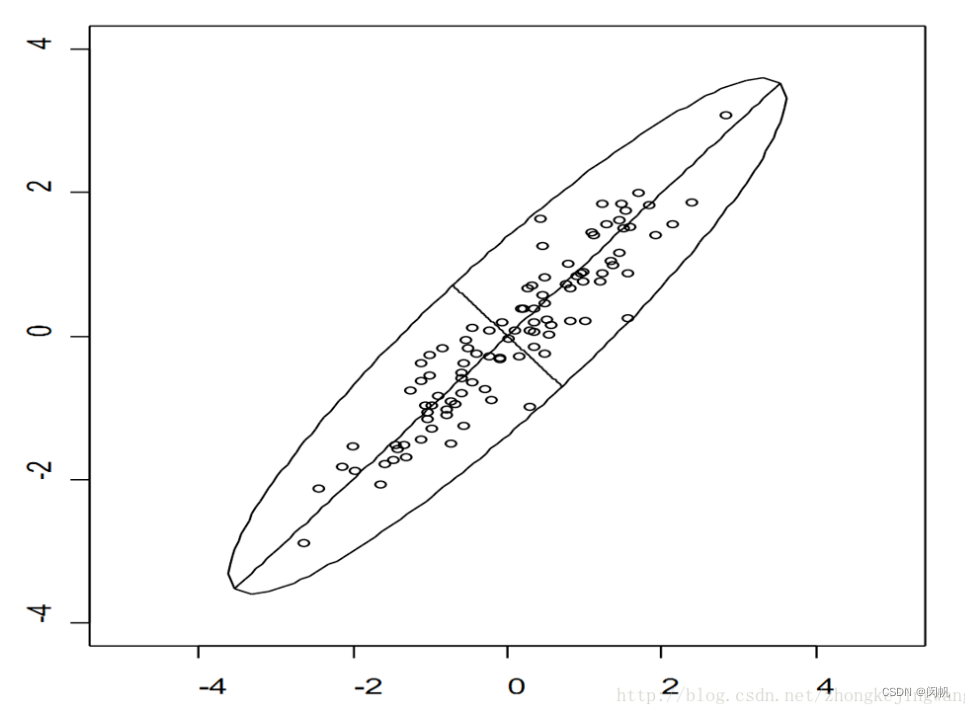
如图 1 所示, 二维平面上有一系列数据点. 从它们的角度来看,
x
x
x 轴和
y
y
y 轴两个特征的区分能力都差不多, 特征的取值范围都是
[
−
4
,
+
4
]
[-4, +4]
[−4,+4].
然而, 如果我们将这些点围绕原点顺时针旋转 45 度, 就会发现新的
x
x
x 轴把样本分得比较开, 而新的
y
y
y 轴区分能力比较弱.
再想像一个极端的情况: 这些点全部在一条直线上, 经过旋转后
x
x
x 轴起到作用, 而
y
y
y 轴完全没有区分能力.
从高等数学的角度, 就是需要求一组正交基, 且排名靠前的基向量 (被称为 主成分) 区分能力更强. 这组正交基的个数有可能少于原始空间的维度, 这时就达到 特征提取 + 降维 的作用.
为了进一步地降维, 设置一个阈值, 将基向量的区分度低于该域值时, 就可以把它抛弃.
3. 优缺点
优点
- 有良好的数学基础;
- 有良好的应用.
缺点:
- 只是一个线性模型;
- 只能做简单的数据预处理;
- 无监督模型, 不一定适用于有监督数据.