主啊,我甚至不知道从何说起...欢迎来到费米悖论。

外面有太多令人恐惧的事物。

我不会一一说过。然而,我读到的一件事情让我感到恐惧,我希望它也让你感到恐惧。 那么,就是这样...

这一切与一个问题有关:如果他们确实存在,为什么还没有来访?可怕的就是这些可能性。 根据《弄清外星人是否存在:解决费米悖论的可能性》:

卡达舍夫定律:

1964年,苏联天文学家和SETI研究员尼古拉·卡达舍夫提出了一种根据物种的技术发展水平对其进行分类的方法。产生的定律有三个层次(或类型),用于根据物种可以利用的能量量对其进行分类。

按定义,第一类型文明(也称为“行星文明”)是那些已经开发出利用和储存其母星全部能量的手段的文明。根据卡达舍夫的说法,这将达到每秒4×1019赫兹的消耗,很可能是在全球范围内采取聚变能、反物质和可再生能源的形式。

下一步是第二类型文明(“恒星文明”),它们的进化程度已经达到可以收获其恒星发出的全部能量——卡达舍夫推测这可能涉及戴森球这样的结构。在这种情况下,这将达到每秒4×1033赫兹的消耗。

第三类型文明(“银河系文明”)是那些能够利用整个银河系的能量的文明,这将达到每秒4×1044赫兹的能量消耗。 鉴于宇宙已经存在138亿年,而我们的太阳系只存在于最近的46亿年,似乎至少会有几个文明能达到第三类型的发展水平。即使我们拥有温和的手段,人类也很难错过这样一个文明的迹象。

所以,我们再次被迫问为什么我们在宇宙中没有找到任何智能生命的迹象。为什么智能生命似乎如此可能,而证据却如此缺乏?这就是事情变得特别有趣、可怕且令人难以置信的地方。

哈特-蒂普勒猜想和“大过滤器”假说:

显而易见的答案是:外星智慧生物简单地不存在。这是美国天体物理学家迈克尔·哈特在1975年发表的论文《地球上缺乏外星人的解释》中提出的结论。

数学家弗兰克·J·蒂普勒在1979年的研究《外星智能生物不存在》中进一步阐明了这一论点。在被命名为哈特-蒂普勒猜想的论点中,他们认为如果任何外星文明已经开发了星际旅行的手段,他们现在已经访问过太阳系了。

另一种可能性是经济学家罗宾·汉森在他1998年发表的网上论文《大过滤器——我们差不多过了吗?》中提出的。正如他总结自己的论点:

“人类似乎有光明的未来,即有非零的机会扩散至填满宇宙的持久生命。但事实上,我们附近的空间现在似乎死气沉沉,这告诉我们任何给定的

这就是卡达舍夫定律发挥作用的地方,它帮助我们根据使用的能量量将智能文明分为三大类。

首先,让我向你解释一个假设的事情...

根据费米悖论——等等,为什么,有许多方式来看待这个问题。

我们的太阳在宇宙的生命周期中相对年轻。有更老的恒星和更古老的类地行星,理论上说,这意味着比我们自己更先进的文明。例如,让我们将我们45.4亿年的地球与假设的80亿年的X星球进行比较。

如果X星球的故事与地球类似,让我们看看他们的文明今天会在什么位置(使用橙色时间跨度作为参考,以显示绿色时间跨度有多大):

比我们先进1000年的文明的技术和知识对我们来说可能使人震惊,就像我们的世界对中世纪人来说一样。比我们先进100万年的文明对我们来说可能难以理解,就像人类文化对黑猩猩来说一样。而X星球比我们先进34亿年...

第一类型文明有能力利用其行星上的全部能量。我们还没有达到第一类型文明,但我们很接近(卡尔·萨根为这个量表创建了一个公式,将我们定为0.7类型文明)。

第二类型文明可以利用其母恒星发出的全部能量。我们微不足道的第一类型大脑几乎无法想象如何做到这一点,但我们已经尽最大努力想象过诸如戴森球之类的东西。

第三类型文明远远超过其他两种类型,获得与整个银河系comparable的能量。

如果这种进步程度听起来难以置信,请记住上面的X星球和他们34亿年的进一步发展。如果X星球上的文明类似于我们的文明,并能够生存到第三类型级别,那么自然的想法是他们现在可能已经掌握了星际旅行,甚至可能已经殖民了整个银河系。

关于星系殖民如何发生的一个假说是,创建可以前往其他行星的机器人,利用新行星上的原材料自我复制约500年,然后发送两个复制品去做同样的事情。即使不接近光速旅行,这个过程也会在375万年内殖民整个星系,在谈论十亿年的时标下,这只是一个相对的眨眼之间:

来源:《科学美国人》:“他们在哪里”

继续推测,如果1%的智能生命得以生存足够长时间成为可能殖民星系的第三类型文明,我们上述的计算表明,光是我们星系就至少有1000个第三类型文明——鉴于这样一个文明的力量,他们的存在很可能是相当显著的。然而,我们什么也看不到,什么也听不到,也没有人来访。

那么,每个人都去哪儿了?

我们对费米悖论没有答案——我们能做的最好的就是“可能的解释”。如果你问十个不同的科学家他们对正确解释的直觉是什么,你会得到十个不同的答案。当你听说过去的人类争论地球是否圆形,太阳是否围绕着地球转,还是认为闪电是宙斯造成的,他们似乎那么原始

果这种理论正确,那么最重要的问题是,在时间轴上大过滤器出现在哪个位置?

事实证明,就人类的命运而言,这个问题非常重要。根据大过滤器出现的位置,我们面临三种可能的现实:我们非常罕见,我们是第一个,或者我们遭殃了。

1. 我们非常罕见(大过滤器在我们身后)

我们的一个希望是大过滤器在我们身后——我们设法超越了它,这意味着生命达到我们的智力水平是极其罕见的。下图显示只有两个物种超越了它,我们就是其中之一。

这种情景可以解释为什么不存在第三类型文明...但这也意味着我们现在已经走了这么远,也许是少数几个例外之一。这意味着我们有希望。表面上,这听起来有点像500年前的人认为地球是宇宙的中心——这意味着我们是特殊的。

然而,科学家称为“观察选择效应”的东西表明,任何在考虑自己的罕见性的人本质上都是一种智慧生命的“成功故事”——无论他们实际上是罕见还是相当普遍,他们思考的想法和得出的结论会是相同的。这迫使我们承认特殊性至少是一种可能性。

如果我们真的特殊,我们究竟在什么时候变得特殊——也就是说,我们超越了几乎所有其他人都困在哪一步? 一种可能性是:大过滤器可能就在一开始——生命开始本身就可能非常不寻常。

这是一个候选项,因为地球存在了10亿年才最终发生,而且我们已经广泛地试图在实验室里复制这一事件,却从未能做到。如果这确实是大过滤器,那么这不仅意味着外面没有智能生命,甚至可能没有其他生命。

另一种可能性是:大过滤器可能是从简单的原核细胞到复杂的真核细胞的跃变。原核细胞形成后,它们保持原状近20亿年,然后才发生进化跃迁,变得复杂并有细胞核。

如果这是大过滤器,那么宇宙四处都是简单的原核细胞,几乎没有其它东西。

还有许多其他可能性——有人甚至认为我们最近取得的进展到当前的智力是一个大过滤器的候选项。

虽然从半智慧生命(黑猩猩)到智慧生命(人类)的跃迁乍看起来不像一件神奇的事,但史蒂文·平克拒绝接受进化的“必然上升”理论:“由于进化并不追求目标而只是偶然发生,它使用最适合给定生态位的适应性,迄今为止在地球上只发生一次的这种结果可能表明,自然选择的这种结果是罕见的,因此绝不是生命之树进化的必然发展。”

大多数跃迁不符合大过滤器候选资格。任何可能的大过滤器必须是十亿分之一的事情,需要发生一次或多次完全意外的事件,提供一个疯狂的例外——因此,像从单细胞到多细胞生命的跃迁这样的事情就被排除在外,因为在这个行星上仅此而已,它已经发生过多达46次的孤立事件。出于同样的原因,如果我们在火星上发

3. 我们将要遭殃了(大过滤器在我们前面)

如果我们既不罕见也不早,第1组思想者会得出结论,大过滤器必定在我们的未来。这表明生命定期进化到我们现在的程度,但几乎在所有情况下,某些东西阻止生命进一步发展并达到高度智能——我们不太可能成为例外。

一个可能的未来大过滤器是定期发生的灾难性自然事件,比如上述提到的伽马射线暴,只是很遗憾地还没有结束,地球上的一切生命很快就会被其中一个摧毁,这只是时间问题。另一个候选者是,几乎所有的智慧文明在达到一定的技术水平后,最终都会自毁的可能性。

这就是为什么牛津大学哲学家尼克·博斯特罗姆说“没有新闻就是好消息”。即使发现火星上的简单生命,也会让我们身后一些潜在的大过滤器不复存在,这将是毁灭性的。而且如果我们发现火星上复杂生命的化石,博斯特罗姆说这“无疑将是有史以来报纸头版上印刷的最坏消息”,因为这意味着大过滤器几乎肯定在我们前面——最终注定我们这个物种的命运。博斯特罗姆认为,就费米悖论而言,“夜空的寂静是金色的”。

解释组2:第二和第三类智能文明确实存在——我们可能没有听说他们的逻辑原因。

组2的解释排除了我们罕见、特殊或在任何事情上首先的任何概念——相反,他们信奉平庸原理,其起点是我们的星系、太阳系、行星或智力水平没有任何不寻常或稀有的地方,除非有证据证明相反。

他们也不太容易假设更高级的智慧生物不存在的缺乏证据就是它们不存在的证据——他们强调我们搜索信号的范围仅仅延伸到我们之外约100光年(星系的0.1%),并提出了许多可能的解释。这里有10个可能:

可能性1)

超级智慧生命很可能已经访问过地球,但在我们出现之前。从整体来看,知觉人类只存在了约5万年,这只是一瞬间的时间。如果接触发生在那之前,它可能只会让一些鸭子翻滚起来并跑进水里,就此结束。此外,书面历史只能追溯到5500年前——一群古代猎人采集者部落可能经历过一些疯狂的外星事件,但他们没有好办法告诉未来的任何人。

可能性2)

星系已经被殖民,但我们只住在星系的一些荒凉的乡村地区。在加拿大北部一个小小的因纽特部落的人意识到发生这种情况之前,欧洲人可能早已殖民了美洲。更高级物种之间恒星居住的城市化可能包含某个区域内所有相邻的太阳系被殖民和沟通,处理随机去我们生活的螺旋臂偏远地区将是不切实际和无目的的。

可能性3)

物理殖民的整个概念对更高级的物种来说是荒谬可笑的。还记得上面第二类型文明围绕其恒星的球体图吗?有了那么多能量,他们可能已经为自己创造了一个完美的环境,满足他们的每个需要。

他们可能已经发展出极其先进的方法来减少资源需求,并且对离开自己幸福的乌托邦去探索冷冷的、空荡荡的、未开发的宇宙毫无兴趣。

一个更先进的文明可能会视整个物质世界为一个可怕的原始地方,早已征服了自己的生物学,并将大脑上传到一个虚拟现实、永生天堂。生活在生物学、死亡、欲望和需求的物质世界中,在他们看来可能像我们看待生活在寒冷、黑暗的大海中的原始海洋生物一样。顺便说一句,思考另一种生命形式已经战胜了死亡,这使我感到无比的嫉妒和沮丧。

可能性4)

外面有可怕的掠食文明,大多数智慧生命知道最好不要广播任何外发信号和广告自己的位置。这是一个令人不快的概念,可以解释我们没有接收到SETI卫星的任何信号。

这也意味着我们可能是超级天真的新手,通过广播外发信号做了难以置信的愚蠢和冒险的事情。目前正在进行关于我们是否应该参与METI(向外星智力发送消息——相反的SETI)的讨论,大多数人说我们不应该。

斯蒂芬·霍金警告说:“如果外星人访问我们,结果会像哥伦布登陆美洲一样,对原住民不利。”即使是卡尔·萨根(一般认为任何足够进步可以星际旅行的文明都会利他,而不是敌对)也称METI实践为“极其不明智和不成熟”,并建议“在这个陌生而又不确定的宇宙中最新的孩子应该安静地听很长时间,耐心地了解宇宙,并比较笔记,然后在我们不理解的未知丛林中吓的大喊大叫”。

可能性5)

只有一个更高智能生命的实例——一个“超级掠食者”文明(就像人类在地球上一样),比其他所有人都更先进,并通过消灭一旦超过一定水平的任何智慧文明来维持这种状况。

这会很糟糕。它的工作方式可能是,消灭所有新兴的智慧生命是资源的低效利用,也许因为大多数会自然消亡。但是超过一定限度,超级生物会采取行动——因为对于他们来说,一个新兴的智慧物种就像一种病毒,随着它开始生长和传播。

这一理论表明,第一个达到星系智慧的物种赢了,现在没人有机会了。这可以解释外面缺乏活动,因为它会使超级智慧文明的数量保持在一个。

可能性6)

外面有大量的活动和噪音,但我们的技术太原始,我们正在寻找错误的东西。就像走进现代办公大楼,打开对讲机,听不到任何活动(当然你听不到, 所以问题不在于我们无法用我们的技术捕捉来自X星球的信号,而是我们甚至无法理解来自X星球的生物是什么或他们想要做什么。

这超出了我们的理解,即使他们真的想启发我们,这也像试图向蚂蚁解释互联网一样。

在这方面,这也可能是对“嗯,如果有那么多花哨的三型文明,为什么他们还没有联系我们?”的答案。为了回答这个问题,让我们问我们自己——当皮萨罗进入秘鲁时,他有停下来过蚁丘试图沟通吗?

他是否慷慨大方,试图帮助蚁丘中的蚂蚁?他是否变得敌对并放慢原来的任务,以粉碎蚁丘?或者蚁丘对皮萨罗来说是完全的、彻底的和永恒的无关紧要?这可能是我们这里的情况。

可能性10)我们对现实的看法完全错误。我们可能与我们所想的一切完全脱节,有许多方式。宇宙可能表面上是一种方式,实际上是另一种方式,比如全息影像。

或者我们可能是外星人,被植入这里作为实验或作 fertilizer 的一种形式。甚至有可能我们都是另一个世界的某个研究人员的计算机模拟的一部分,其他生命形式简单地没有编程进模拟。

我的确为其中一些东西感到害怕。

模拟大数定律

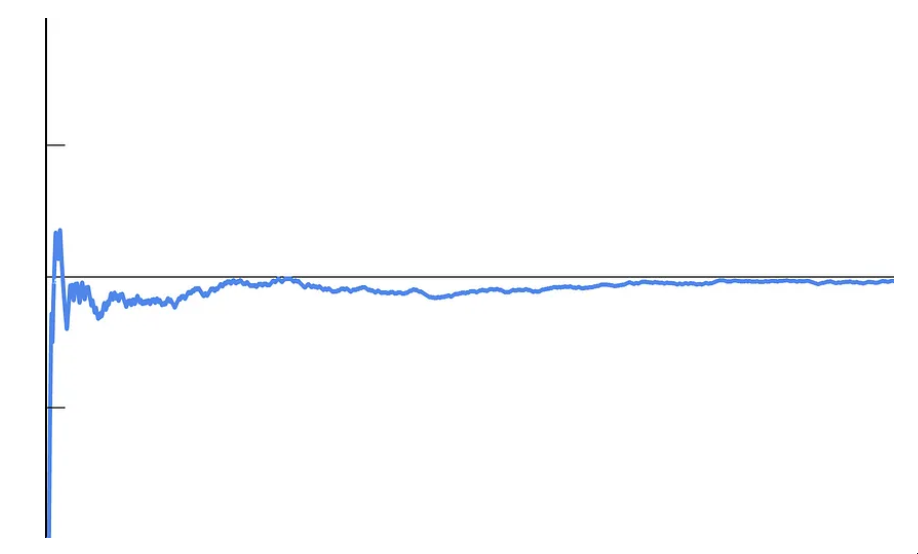大数定律的可视化

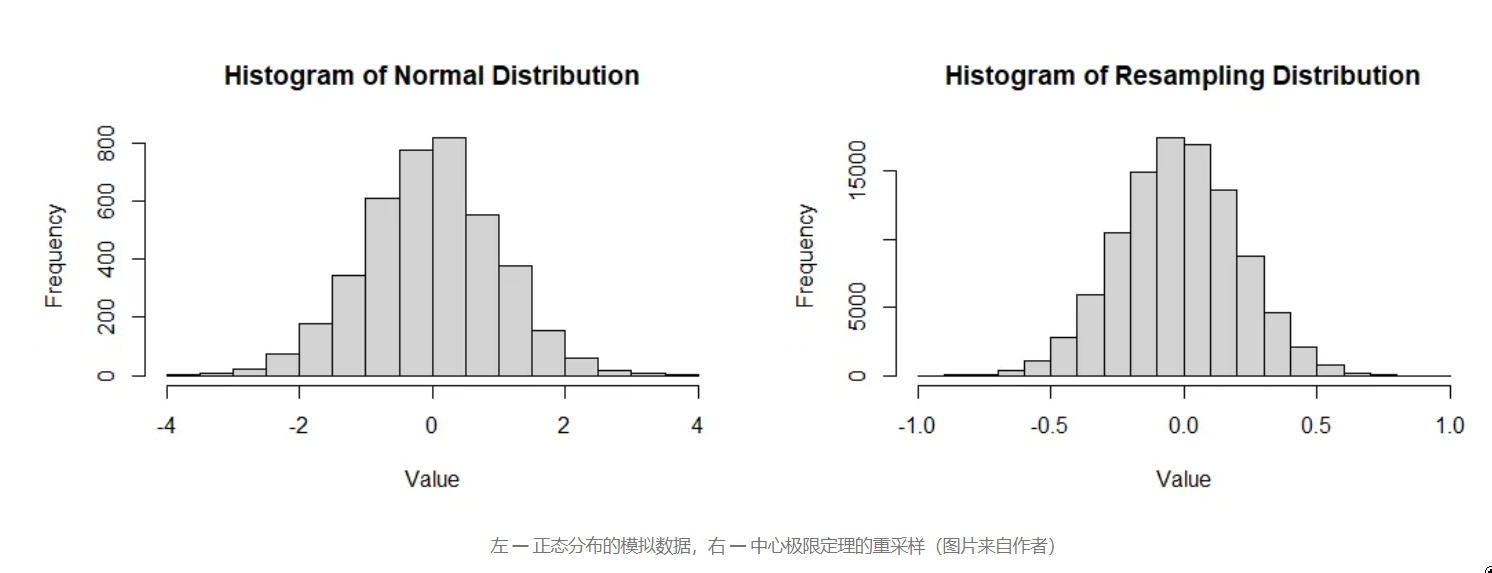
为了证明大数定律，我们将执行 LLN 以实现均匀分布。对于每次重采样，我们将计算样本均值和样本标准差。

二项分布 二项分布 是 n > 1 的伯努利分布。二项分布计算只有两种可能结果（二进制）的事件的概率 - 通常是成功或失败。

二项分布的概率质量函数

对于二项分布，我们生成了 4，000 个参数为 n 500 且 p 为 0.7 的样本。总体均值为 349.883，标准差为 10.36722。

然后对于 CLT，我们使用替换重新采样 100，000 个样本均值，得到 100，000 个样本均值的总体均值为 349.8797，而标准差为 2.307338。

# 4 Binomial Distribution
x = rbinom(n = 4000, size = 500, prob = 0.7)
hist(x = x,
     main = 'Histogram of Binomial Distribution',
     xlab = 'Value')
mean(x)
sd(x)
dist = replicate(n = sample_mean,
                 expr = mean(sample(x = x,
                                    size = sample_size,
                                    replace = TRUE)))
hist(x = dist,
     main = 'Histogram of Resampling Distribution',
     xlab = 'Value')
mean(dist)
sd(dist)
sd(x) / sqrt(sample_size) # Proven

参数

对于模拟，我们为随机发生器设置种子。然后对于重采样，我们设置两个参数：1234

sample_mean = 100000
# 创建 100，000 个带有替换的样本

sample_size = 20
#意味着对于每次重采样，我们取 20 个样本并计算平均值和标准偏差

# Parameters
sample_mean = 100000
sample_size = 20
set.seed(1234)

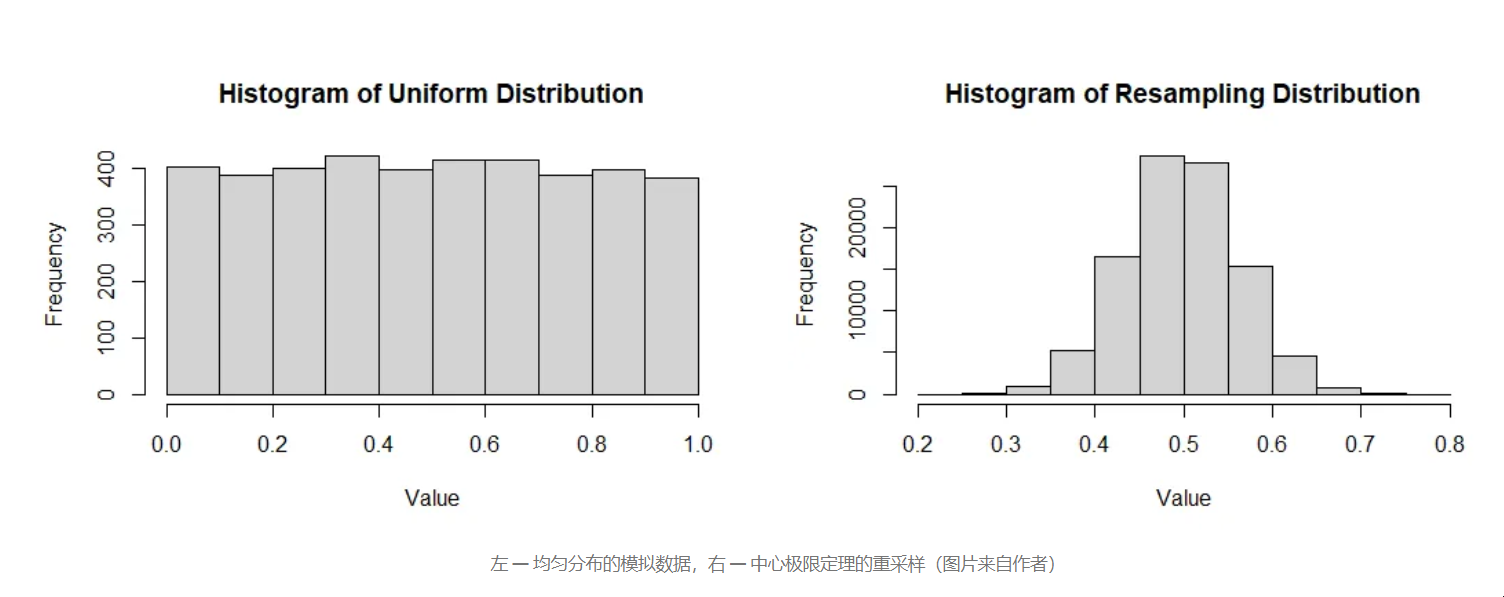
均匀分布

对于均匀分布，我们生成 4,000 个样本，

参数最小值A 为 0，最大值 B 为 1。

它将是概率分布。

总体均值为 0.5016619，而标准差为 0.2892354,方差为 0.08365712

# Uniform Distribution
x = runif(n = 4000, min = 0, max = 1)
hist(x)
mean(x)
sd(x)
# Resampling
dist = replicate(n = sample_mean,
                 expr = mean(sample(x = x,
                                    size = sample_size,
                                    replace = TRUE)))
hist(dist)
mean(dist)
sd(dist)
sd(x) / sqrt(sample_size) # Proven

当 n 增长时，样本均值将缓慢收敛到总体均值 0.5016619。这意味着证明样本均值总体均值的概率接近μ等于 1 的定理被证明！

# Means
mean(x)
means = cumsum(dist)/(1:sample_mean)
# Data viz
ggplot(data = data.frame(x = 1:sample_mean, 
                         y = means))+
  geom_line(aes(x = x,
                y = y),
            color = 'red',
            size = 1.5)+
  geom_hline(yintercept = mean(x))+
  labs(x = 'Number of observations',
       y = 'Cumulative mean')+
  theme_minimal()

样本均值收敛

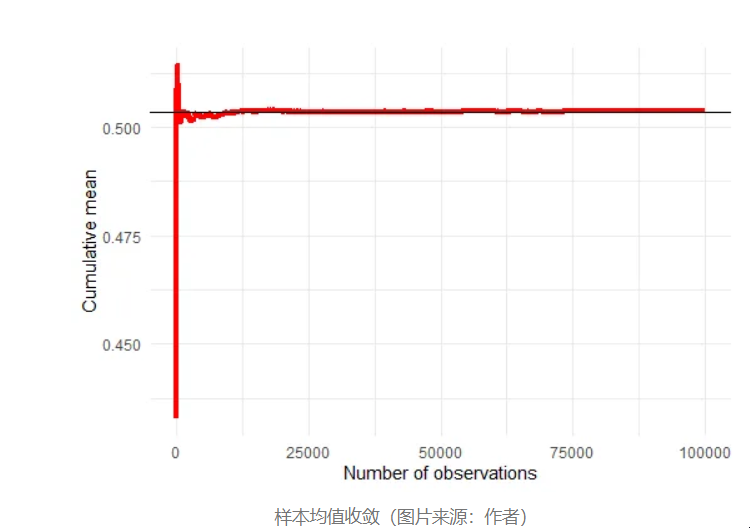
样本均值收敛

我们通过对总体进行重采样并计算其标准差来模拟样本方差。然后，当 n 增长时，样本方差将缓慢收敛到总体方差 0.08365712。

# Variance
sd(x)
stdev = replicate(n = sample_mean,
                  expr = sd(sample(x = x,
                                   size = sample_size,
                                   replace = TRUE)))
mean(stdev)
variance = cumsum(stdev ^ 2)/(1:sample_mean)
# Data viz
ggplot(data = data.frame(x = 1:sample_mean, 
                         y = variance))+
  geom_line(aes(x = x,
                y = y),
            color = 'red',
            size = 1.5)+
  geom_hline(yintercept = mean(variance))+
  labs(x = 'Number of observations',
       y = 'Cumulative variance')+
  theme_minimal()

样本方差收敛

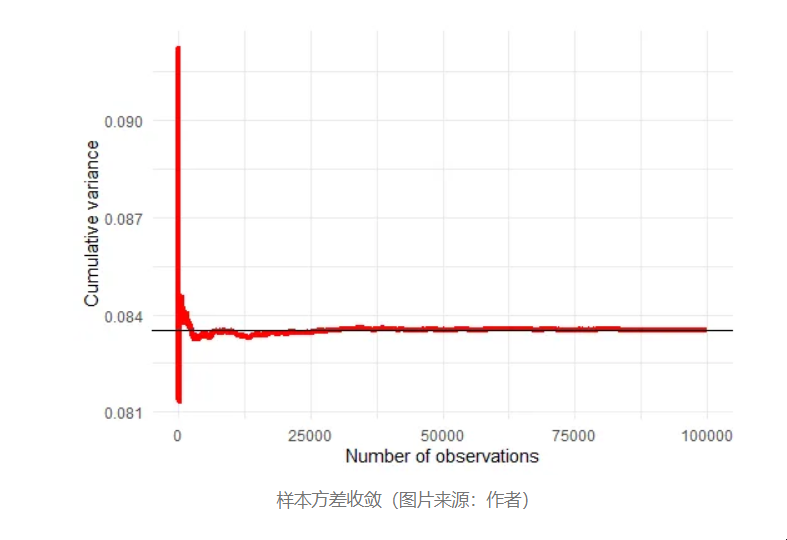
样本方差收敛

LLN模拟的完整代码附后

# ---------- Law of Large Number ----------
# Install packages
install.packages('ggplot2')
library(ggplot2)
# Parameters
sample_mean = 100000
sample_size = 20
set.seed(1234)

# Uniform Distribution
x = runif(n = 4000, min = 0, max = 1)
hist(x)
mean(x)
sd(x)
# Resampling
dist = replicate(n = sample_mean,
                 expr = mean(sample(x = x,
                                    size = sample_size,
                                    replace = TRUE)))
hist(dist)
mean(dist)
sd(dist)
sd(x) / sqrt(sample_size) # Proven

# Means
mean(x)
means = cumsum(dist)/(1:sample_mean)
# Data viz
ggplot(data = data.frame(x = 1:sample_mean, 
                         y = means))+
  geom_line(aes(x = x,
                y = y),
            color = 'red',
            size = 1.5)+
  geom_hline(yintercept = mean(x))+
  labs(x = 'Number of observations',
       y = 'Cumulative mean')+
  theme_minimal()

# Variance
sd(x)
stdev = replicate(n = sample_mean,
                  expr = sd(sample(x = x,
                                   size = sample_size,
                                   replace = TRUE)))
mean(stdev)
variance = cumsum(stdev ^ 2)/(1:sample_mean)
# Data viz
ggplot(data = data.frame(x = 1:sample_mean, 
                         y = variance))+
  geom_line(aes(x = x,
                y = y),
            color = 'red',
            size = 1.5)+
  geom_hline(yintercept = mean(variance))+
  labs(x = 'Number of observations',
       y = 'Cumulative variance')+
  theme_minimal()