目录

一.标量函数和矢量函数

二.矢端曲线

三.矢量函数导数和微分

1.导数

 2.导数的几何意义

3.微分

4.矢量导数性质

5.例题

四.矢量导数的应用

1.几何应用 

1.曲线的切线和法平面

2.曲面的法线和法平面

2.物理应用

3.两大典型问题

五.矢量函数的积分

---

如果第一章我们引入了矢量，指的都是常矢量，那本章我们讨论的就是变化的矢量，即矢量函数.

研究矢量函数的这个话题，我们称之为矢量分析

通俗点讲，矢量 + 对时间t的微积分 = 矢量分析

由此，运动进入了矢量理论，我们所熟知的变速度v,变加速度a等等都是我们研究的典型例子.

一.标量函数和矢量函数

标量函数我们在中学的时候已经接触过

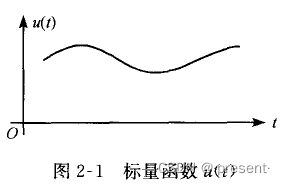
随着自变量t的变化， 都会有唯一一个因变量u(t)与之对应，我们称作为函数

标量顾名思义，它并不涉及方向，仅仅是与参数t相关，仅涉及值的变化，所以我们称之为标量.

那如何表示一个变化的矢量呢？

前面我们提到过，一个矢量的本质就是对构成它的单位矢压伸并相加的过程(单位矢的线性组合)

所以矢量函数，我们可以自然的联想到，假如它对应的单位矢的变化，本身就是一个标量函数，则

可以将矢量与t的变化，看作每一个单位矢随t的变化(一个标量函数)，再线性组合，这样我们就自

然而然可以推导出矢量函数的定义

矢量函数的每一个对应分量，是一个标量函数，且三者两两独立，互不影响 

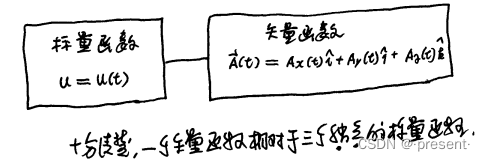
二.矢端曲线

但是仅仅说每一个分量都是一个随t变化的标量函数，还是很抽象,我们需要借助图来实现数形结合.

我们研究力，加速度等等，都是一个三维的向量,三维是有助于几何表示的.(四维,n维等更高维的运

动我们还没研究出来)

于是我们退一步，将向量仅仅用三个分量表示，几何至此进入了矢量函数.

我们把以坐标o为原点，终点M随t在变化的变曲线称作为矢端曲线.

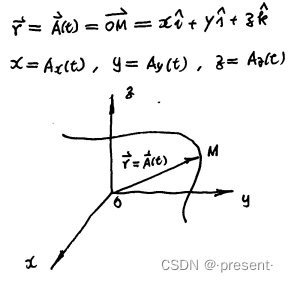
一个很典型的例子，就是我们熟知的螺旋线

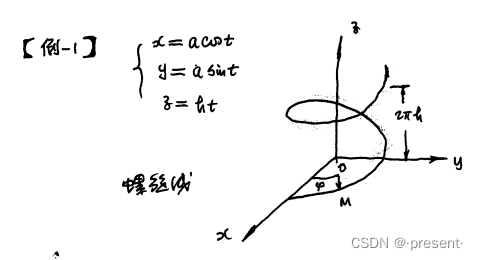
它对应的矢量函数，我们也可以直接写出来

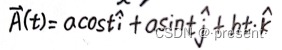
三.矢量函数导数和微分

1.导数

标量函数的导数，我们已经很熟悉了，利用的就是逼近的思想. 

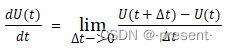
类比于标量函数的导数，我们也可以得到矢量函数的导数.

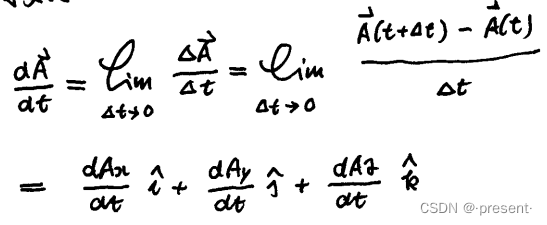
也就是分别对每一项的标量函数对t进行求导即可.

还可以简写为另一种形式

当然看上去很容易理解，不过其中却隐含着一个条件.

也就是在正交直角坐标系中，单位矢是不随时间t变化而变化的，在其它坐标系就未必是这样的情

况.(如果随时间t变化而变化，则每一个分量求导，会出现两项，比如说分别对Ax求导,单位矢不求

导，加上对Ax不求导，单位矢求导)

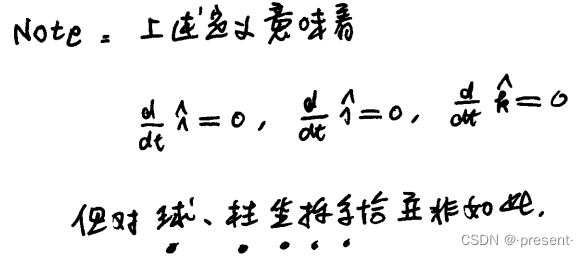
举一个具体的例子，像上面我们所举的例子，对螺旋线进行求导，就是对每一个分量进行求导.

  

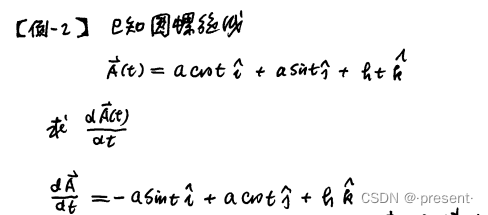
 2.导数的几何意义

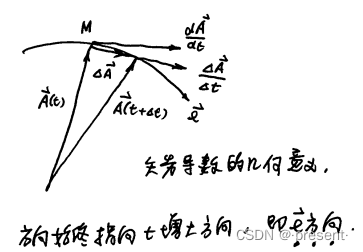
矢量函数的导数，我们需要借助矢端曲线来理解.

分式部分的两个矢量相减，实际上仍旧是一个矢量，当变化时间t无限趋近于0时，得到的矢量，实

际上是矢端曲线的切线，方向始终指向t增加的方向.

3.微分

我们依旧从标量函数出发，进而引入矢量函数的微分.

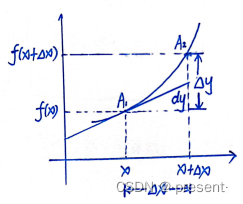
标量函数的增量我们表示为下面这种形式，自变量变化后对应的因变量相减就是标量函数的增量.

 现在我们想要将增量用另一种形式表示，或者更具体来说，近似

用什么方法来近似呢？微积分的思想，化曲为直，于是我们想到用直线去近似，用均匀表示非均匀

我们把增量表示为下面这种形式

其中我们把前面的部分就称为标量函数在点x0处相对于自变量增量x的微分，记为

  

但是我们不能说微分就等同于标量函数的增量，这只是一种近似，两者之间相差一个高阶无穷

小，像图中的dy很明显就不等同于标量函数的增量.

但是在x变化无限趋近于0时，高阶无穷小的一项，就无限逼近于0，这时候我们就可以用dy来近似

等同于标量函数的变化.像图中的A2点无限靠近A1点时，就会有

此时

得到最终dy的具体表达式，  

由上面的表达式我们也可以知道什么是微分？

微分是函数改变量的线性主部，线性是由于它表示的形式是一个一次函数的形式，A是一个常数，

等于该点处的导数，主部说明它只是一种近似，而非完全等同.

那具体矢量函数的微分要如何定义呢？

同样的，有了标量函数的微分，而矢量函数中存在三个标量函数，分别对其求微分就是矢量函

数的形式,下面的式子只是把dt乘过去式子右边而已.

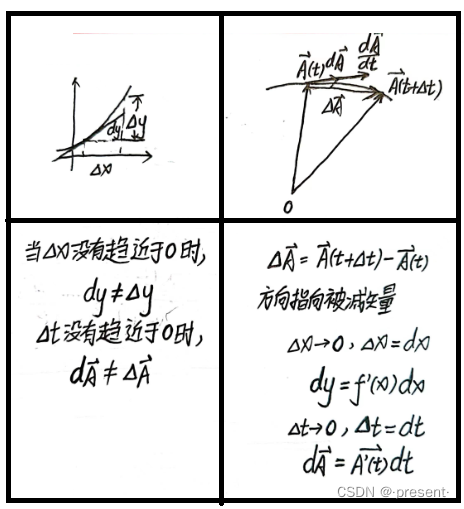
当然，需要注意两者的区别，标量函数求微分得到的是数，但是矢量函数求微分得到的是矢量，它

也有方向，与dt直接相关，如果dt>0，则和矢量函数求导的方向一致，反之，则相反

4.矢量导数性质

由于矢量函数求导，本质是对标量函数求导，所以标量函数求导存在的性质，也都对应存在

比如说常数可以提出，常数求导为0等等,也指出来向量求导一个重要的特性——线性

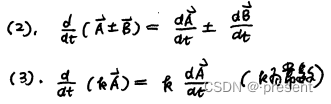
(与之还可以联想到矩阵，矩阵同样也是一种线性运算)

有两点需要注意

第一.假如两个矢量都分别与要求导的变量相关，则需要分别进行求导 

比如，就要先对前面的A矢量求导，后面看作常数，再对后面的A矢量求导，前面看作常数

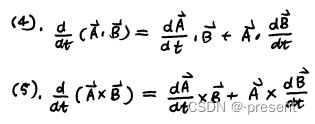
第二.矢量函数求导依旧满足复合函数求导法则

5.例题

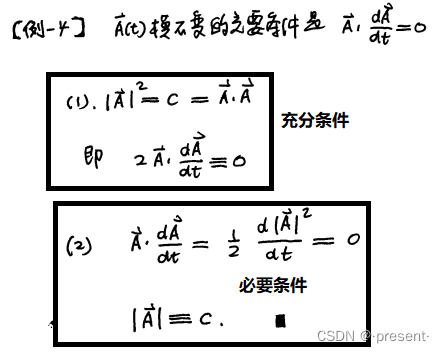
我们知道单位矢的模是始终不变的，所以，由上面的例题，我们还可以得出一个重要的结论

 

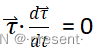
单位矢和其导数相点积，得到的结果为0，两个矢量是正交的. 

四.矢量导数的应用

把握思想：

1.平行矢量，两者对应分量成比例

2.两矢量相正交，点积为0

1.几何应用 

1.曲线的切线和法平面

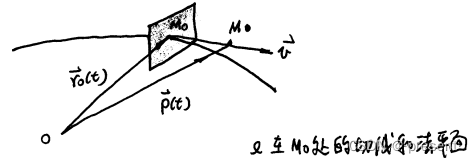
对矢径求导，就是速度的定义

由前面矢量函数的求导我们可以知道，矢径也是矢量，对其求导，它的方向就是对应切线方向 

 引入切线上的动点M，我们知道MM0矢量，必定和速度平行，对应分量成比例，由于动点是变化

的，得到的表达式就是对应的曲线方程

同样的，令M1是法平面上的动点，M1M0矢量必定和速度垂直， 有两矢量相正交，点积为0，

由于动点是变化的，得到的表达式就是对应的曲线法平面方程

2.曲面的法线和法平面

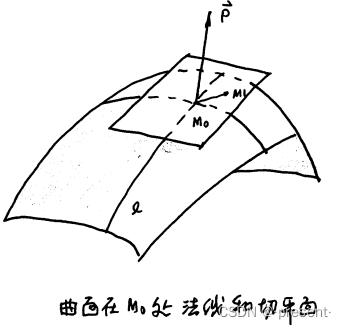
我们先假设出曲线方程F(x,y,z) = 0

根据链式法则，对等式两边分别进行求导，我们就可以得到两个矢量点积的形式

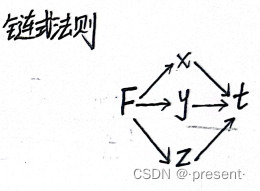
其中后面的我们可以发现，就是我们对应的速度，也就是切线，那和我们切线点积为0的矢量，对

应的就是我们的法线，在后面我们也会提到，这其实就是我们的梯度 

有了法线，准确来说，是和法线方向的矢量，我们同样设其上的一个动点为P，PM0矢量，必定和

法线平行，对应分量成比例，由于动点是变化的，得到的表达式就是对应曲面的法线方程

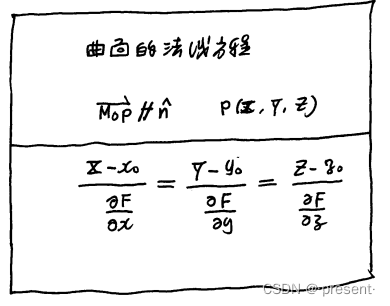
同样的，令M1是法平面上的动点，M1M0矢量必定和法线垂直， 有两矢量相正交，点积为0，

由于动点是变化的，得到的表达式就是对应的曲面的切平面方程

2.物理应用

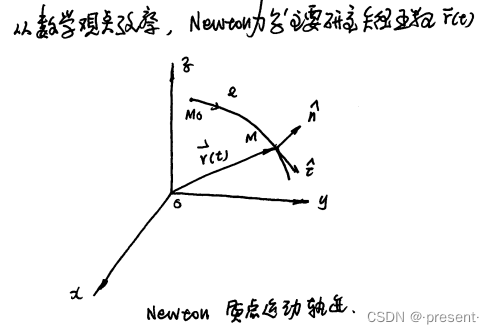
三维直角坐标下，存在着无穷多个位矢，密密麻麻，如果全部画出来，还没分析问题，估计就已经

晕了

所以，我们抽象出来，把矢量和点相对应，坐标单位矢都是相同的，不同的仅仅只是坐标分量

这就是每个点坐标(x,y,z)的来源

从这里也可以看出矢径函数，描绘了三维笛卡尔直角坐标系的位置变化，即质点的运动轨迹

对其求导，得到的切线方向矢量，就是速度

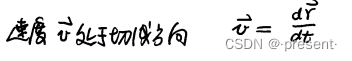
速度除与相应的模，得到的就是切向单位矢

加速度，我们定义对速度求导

切向单位矢，其模长虽然不会随时间发生变化，但是方向不断在改变，所以速度要对时间t求导，

切向单位矢也要对时间t求导 

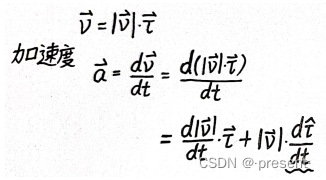
前面的矢量，方向为切线方向，我们称之为切向加速度

那后面的矢量是什么呢？我们依旧需要确定它的方向和大小

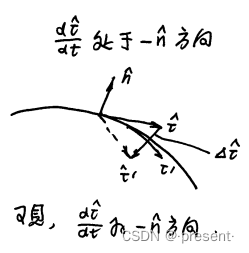
我们可以结合图形来理解， 

PS：箭头指向被减矢量 

当距离不断缩短的时候，我们可以发现的方向其实是与法线相反的方向

不过更为简单的一种理解方法是，前面我们已经得到模长不变的矢量，它满足下面这个表达式

 

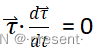
所以 必定为法线方向

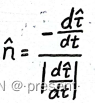
那这个矢量的大小为多少呢？

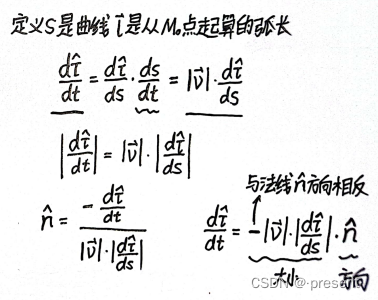
我们最终可以化简出来加速度的表达式

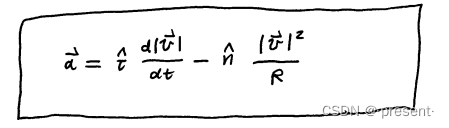
前面一项我们称之为切向加速度，后面一项我们称之为法向加速度 

3.两大典型问题

推广到任意的矢量，而不仅仅是局限于矢径.

不过思想仍然是前面的思想，对应分量成比例，与两矢量点积为0，其相互正交.

五.矢量函数的积分

对每一个分量(标量函数)做积分，就是矢量函数的积分 

不过需要注意，只有在笛卡尔坐标系下的坐标单位矢不参与积分.