👉🏻 直接插入排序

插入排序是一种简单但有效的排序算法，它的基本思想是将一个元素插入到已排序的序列中，从而得到一个新的有序序列。
就像我们打扑克一样，一张一张的模，每摸新的一张放入已经排序好的牌中，在通过简单的对比，放入正确的位置，就能得到新的有序序列。
在这里插入图片描述

代码实现如下：👇🏻

int main()
{
	int arr[] = { 12,34,52,2,4,41,24,6,7,24,15 };
	int sz = sizeof(arr) / sizeof(arr[0]);

	for (size_t i = 1; i < sz; i++)
	{
		int end = i - 1;
		int tmp = arr[i];
		while (end >= 0)
		{
			if (arr[end] > tmp) 
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
				break;
			
		}
		arr[end + 1] = tmp;
	}
	for (size_t i = 0; i <sz; i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

👉🏻 选择排序

这里我们以升序为终点出发思想：
选择排序的基本思想是每次从未排序的序列中选择最小的元素，然后将其放到已排序的序列的末尾。
选择排序的思想其实和直接插入排序很相似，但是我们仔细对比一下，会发现略有不同，直接插入排序中，我们插入一个元素到一个已经排好序的序列当中，此时这个元素是不定的，它比较随机，我们还要将其跟已经排好序的序列进行对比放到适合的位置。
而选择排序不同的是，它插入的这个元素，是经过选择过后的，选择排序从未排序的序列中挑选最小的插入已经排好序的末尾，此时这个最小的元素是已经排好序的序列中最大的了，所以此时无需再去跟已经排好序的序列对比，就省了些功夫。
具体代码实现如下：👇🏻

void Swap(int* x1, int* x2)
{
	int tmp = *x1;
	*x1 = *x2;
	*x2 = tmp;
}
void SelectSort(int arr[], int n)
{
	int i, j;
	for (i = 0; i < n; i++)
	{
		int min = i;
		for (j = i + 1; j < n; j++)
		{
			if (arr[j] < arr[min])
				min = j;
		}
		Swap(&arr[i], &arr[min]);
	}
}
int main()
{
	int arr[] = { 12,34,52,2,4,41,24,6,7,24,15 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	SelectSort(arr, sz);
	for (size_t i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}

	return 0;
}

最小和最大一起插入排序
既然如此，我们还可以顺着这个思想，分别从未排序的序列中寻找最小和最大的值，最小的值插入左侧已经排好序的序列的末尾，最大值插入右侧已经排好序的序列的头部。
具体代码实现如下：👇🏻

void Swap(int* x1, int* x2)
{
	int tmp = *x1;
	*x1 = *x2;
	*x2 = tmp;
}
void SelectSort(int arr[], int n)
{
	int left = 0,right = n-1;
	for (; left < right;)
	{
		int min = left,max = right;
		for (int j = left + 1; j < right; j++)
		{
			if (arr[j] < arr[min])
				min = j;
			if (arr[j] > arr[max])
				max = j;
		}
		Swap(&arr[min], &arr[left]);
		
		Swap(&arr[max], &arr[right]);
		left++;
		right--;
	 }
	
	
}
int main()
{
	int arr[] = { 12,34,52,2,4,41,24,6,7,24,15 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	SelectSort(arr, sz);
	for (size_t i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}

	return 0;
}

👉🏻 希尔排序

希尔排序是一种基于插入排序的排序算法，它的基本思想是将一个大的序列分成若干个子序列，对每个子序列进行插入排序，然后逐步缩小子序列的长度，最终将整个序列排序。希尔排序可以在一定程度上提高插入排序的效率，因为它可以将较小的元素快速移动到正确的位置，从而减少了插入排序中的比较和交换次数。
另外，希尔排序的实现也比较简单，只需要对插入排序进行一些简单的修改即可。
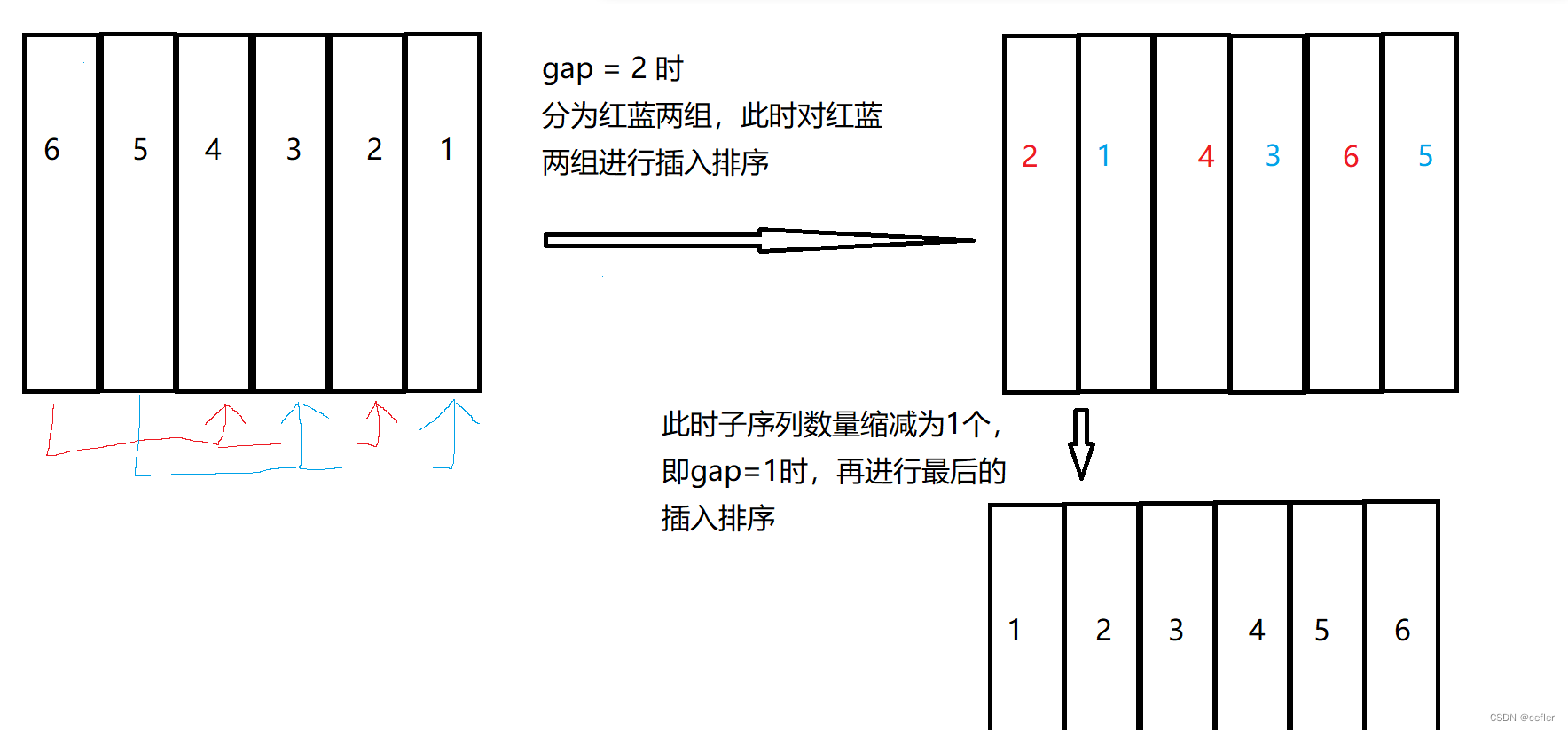
在这里插入图片描述
对于gap的初始值和变化如何定义？ 🤔
我们知道，gap最后的值一定得是1，因为前面分成多个子序列只是为了方便我们快速将序列进行有序化（为了后期统一插入排序减少不必要的比较），但是我们最后要对整个序列还是要再进行插入排序的（即gap ==1）

但是，gap的初始化应该是多少呢？每次gap应该减少多少呢？
首先，我们先了解gap的大小对整个排序的影响:

gap大：有利于大的数据快速排到后面，有利于小的数据快速排到前面
gap小：有利于整体的有序性提升

所以，对于gap的如何初始化，每次减少多少其实并没有明确的规定，各有利弊，这个取决于你。
不过常见的有：
先将gap初始化为n(n为序列的长度)
而后每次gap每次变化：

gap = gap/3+1;加1是为了确保gap最后的值一定是为1
gap = gap/2;

好了，说了这么多，看具体的代码实现👇🏻

void ShellSort(int arr[], int n)
{
	int gap = n;
	while (gap> 1)
	{
		gap = gap / 3 + 1;
		//gap = gap / 2;
		for (size_t i = 0; i < gap; i++)
		{
			for (size_t j = i; j < n - gap; j += gap)
			{
				int end = j;
				int tmp = arr[end + gap];
				while (end >= 0)
				{
					if (arr[end] > tmp)
					{
						arr[end + gap] = arr[end];
						end -= gap;
					}
					else
						break;
				}
				arr[end + gap] = tmp;
			}

		}
	}
	
}