欢迎关注我的CSDN：https://spike.blog.csdn.net/
本文地址：https://blog.csdn.net/caroline_wendy/article/details/130983835

上置信界算法和汤普森采样算法是两种解决多臂老虎机问题的经典方法。多臂老虎机问题是一种探索与利用的平衡问题，即在有限的尝试次数内，如何选择最优的动作（拉动哪根拉杆）来最大化累积奖励。上置信界算法是一种基于置信区间的方法，根据每个动作的期望奖励和不确定性来计算一个上界，然后选择上界最大的动作。汤普森采样算法是一种基于贝叶斯推断的方法，根据每个动作的先验分布和观测数据来更新后验分布，然后，从后验分布中采样一个参数，再根据该参数选择最优的动作。这两种方法都能有效地平衡探索与利用，从而达到较低的累积懊悔。

1. 上置信界算法 (Upper Confidence Bound)

在强化学习的任务重，一个行动的不确定性越大，就越具有探索的价值，探索之后，可能发现的期望奖励很大。上置信界（UCB，Upper Confidence Bound）算法是基于不确定性的策略算法，使用 霍夫丁不等式（Hoeffding’s inequality）。核心思想就是，在已有的期望中，加入不确定性度量 $\hat{U}(a_t)$ ，根据霍夫丁不等式（Hoeffding’s inequality），设置较小概率p，用于超过期望的上界，一般p是随着时间逐渐减少的，可以设置为 $p=\frac{1}{t}$，因此：

$$\begin{gathered} p=e^{-2N(a_t)\hat{U}(a_t{)}^2} \\ \hat{U}(a_t)=\sqrt{\frac{-\log p}{2(N(a_t))}} \end{gathered}$$

$p$ 是最贱减少的概率，$N(a_t)$ 是选择的次数，$U(a_t)$ 是不确定性度量。起始选择次数是0，避免除数为0，额外加1，同时代入 $p=\frac{1}{t}$。

$$\hat{U}(a_t)=\sqrt{\frac{\log t}{2(N(a_t))+1}}$$

则最终的选择策略，由基于期望$\hat{Q}(a)$，转换为基于UCB，$c$ 是系数，用于控制不确定性度量的占比，可以设置为1，即：

$$\begin{gathered} a_t=\arg {max}_{a\in A}[\hat{Q}(a)] \\ {a}_t=\arg {max}_{a\in A}[\hat{Q}(a)+c\cdot \hat{U}(a_t)] \end{gathered}$$

源码如下：

class UCB(Solver):
    """
    UCB 算法，继承 Solver 类
    """
    def __init__(self, bandit, coef, init_prob=1.0):
        super(UCB, self).__init__(bandit)
        self.total_count = 0
        self.estimates = np.array([init_prob] * self.bandit.K)
        self.coef = coef

    def run_one_step(self):
        self.total_count += 1
        ucb = self.estimates + self.coef * np.sqrt(
            np.log(self.total_count) / (2 * (self.counts + 1)))
        k = np.argmax(ucb)
        r = self.bandit.step(k)
        self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
        return k

2. 汤普森采样算法 (Thompson Sampling)

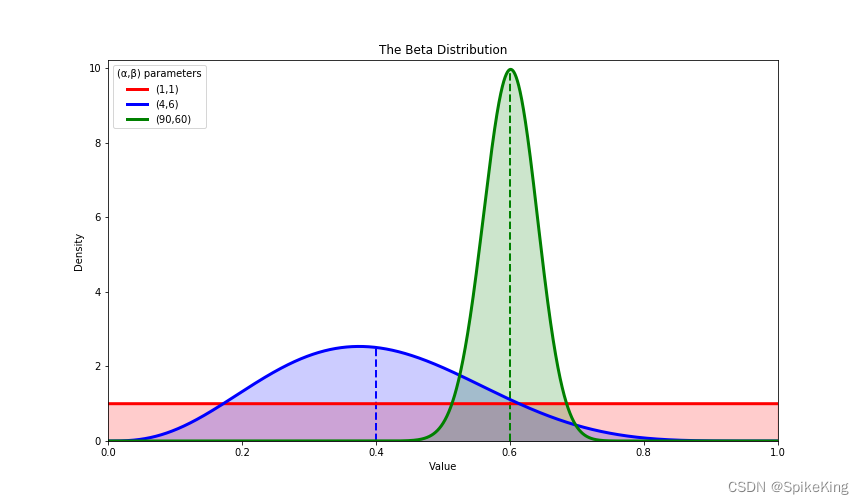
汤普森采样是计算所有拉杆的最高奖励概率的蒙特卡洛采样方法，主要基于Beta分布，不同的期望值，有着不同的采样概率，通过不断修正期望范围，随机采样概率。

源码如下：

class ThompsonSampling(Solver):
    def __init__(self, bandit):
        super(ThompsonSampling, self).__init__(bandit)
        self._a = np.ones(self.bandit.K)
        self._b = np.ones(self.bandit.K)

    def run_one_step(self):
        samples = np.random.beta(self._a, self._b)
        k = np.argmax(samples)
        r = self.bandit.step(k)

        self._a[k] += r
        self._b[k] += 1 - r
        return k

Beta 分布：

Beta 分布是一种定义在 (0,1) 区间的连续概率分布，有两个形状参数 α 和 β，可以用来描述伯努利试验的成功概率的不确定性。Beta分布的概率密度函数为：
$$f(x;\alpha ,\beta )=\frac{1}{B(\alpha ,\beta )}{x}^{\alpha -1}(1-x{)}^{\beta -1}$$ 其中，B(α,β)是Beta函数。与Gamma函数有如下关系：$$B(\alpha ,\beta )=\frac{\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}$$ Beta分布的期望和方差分别为：
$$\begin{gathered} E(X)=\frac{\alpha }{\alpha +\beta } \\ Var(X)=\frac{\alpha \beta }{(\alpha +\beta {)}^2(\alpha +\beta +1)} \end{gathered}$$ Beta分布可以看作是一个概率的概率密度分布，用来建模二项分布和均匀分布之间的关系。