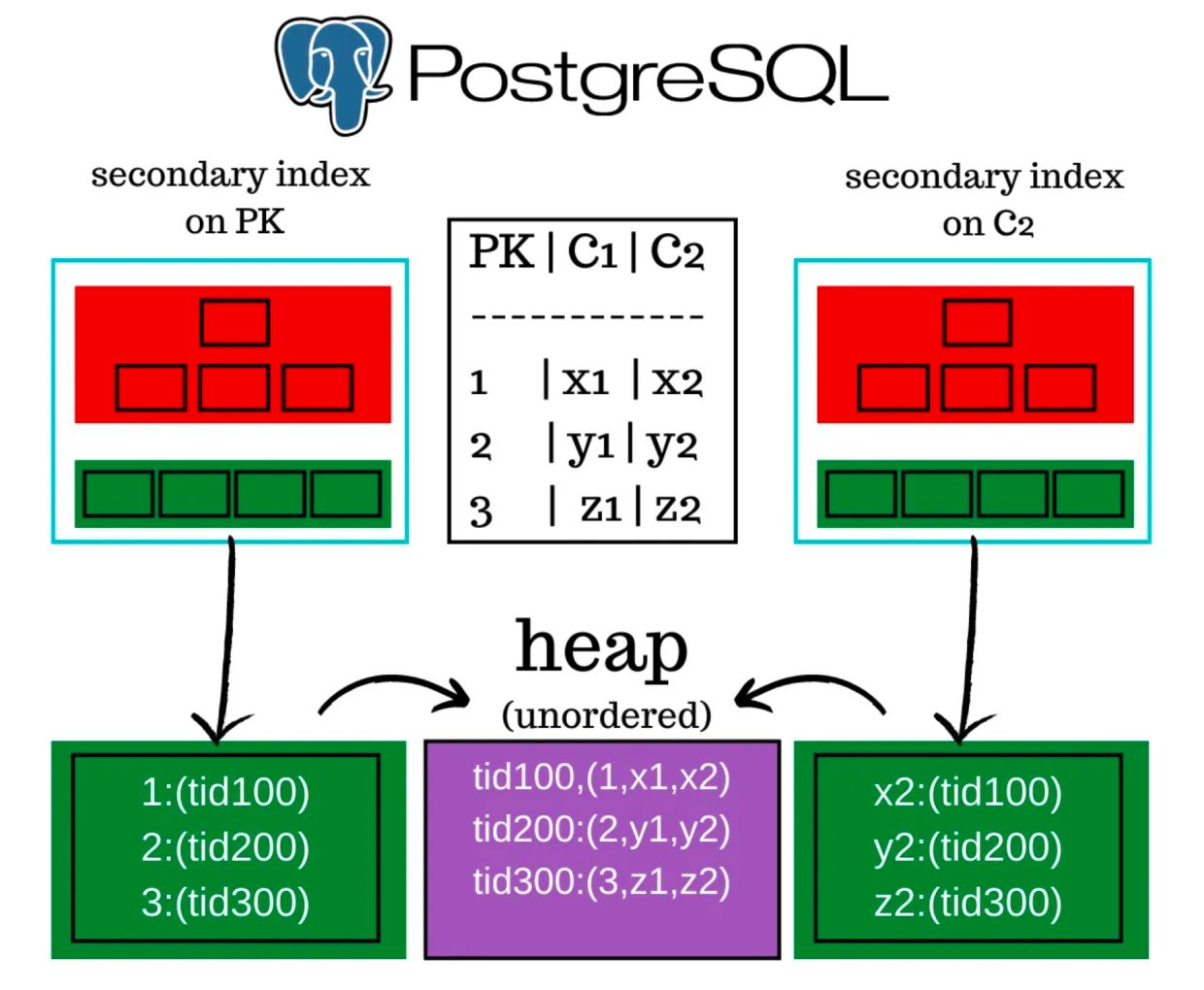
摘要: logistic 回归是使用超平面将空间分开, 一边是正样本, 另一边是负样本. 因此, 它是一个线性分类器.

1. 线性分类器

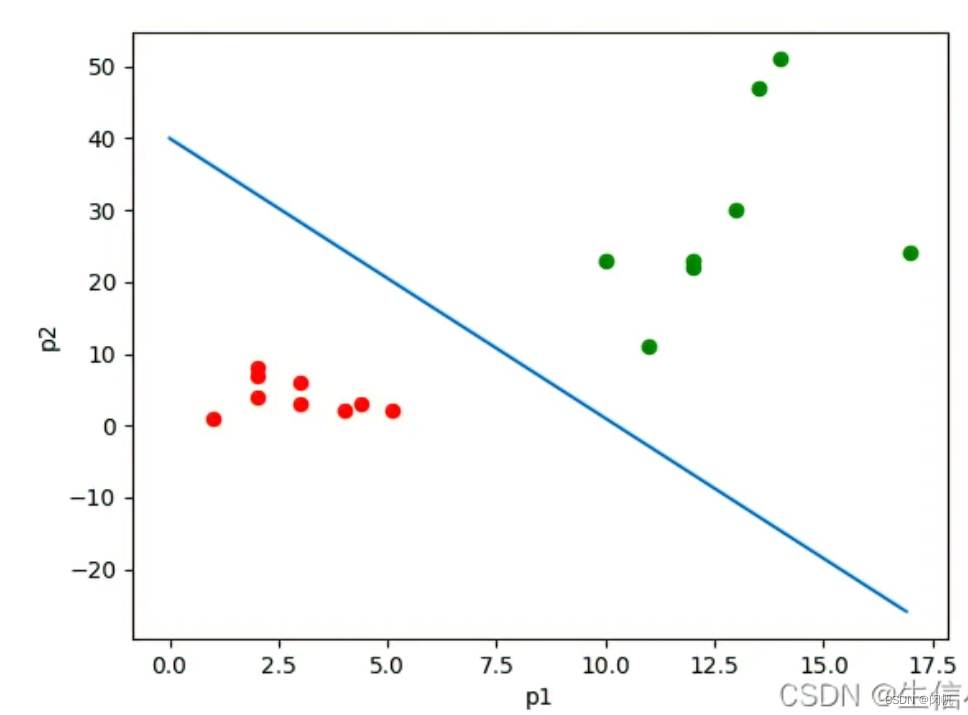
如图 1 所示, 若干样本由两个特征描述, 对应于二维平面上的点. 它们为正样本或负样本, 由不同颜色表示. 现在需要使用一条直线将正、负样本分开. 这样, 对于新的样本, 就看它落在直线的哪一边, 由此判断正负. 这条直线就是线性分类器. 显然, 对于更高维的数据, 其线性分类器就是一个超平面.

图 1. 线性分类器

2. 方案

• 输入: 数据矩阵 $\mathbf{X}=(x_{ij}{)}_{n\times m}\in {\mathbb{R}}^{n\times m}$, 二分类标签向量 Y = ( y i ) n × 1 ∈ { 0 , 1 } n \mathbf{Y} = (y_i)_{n \times 1} \in \{0, 1\}^n Y=(yi​)n×1​∈{0,1}n.
• 输出: $m$ 维空间上的一个超平面 $\mathbf{wx}=0$, 其中 $\mathbf{w},\mathbf{x}\in {\mathbb{R}}^m$.
• 优化目标: $\max {\prod }_{i=1}^{n}h({\mathbf{x}}_i{)}^{y_i}(1-h({\mathbf{x}}_i){)}^{1-y_i}$.

其中 ${\mathbf{x}}_i=(x_{i1},x_{i2},x_{im})$, $h({\mathbf{x}}_i)=\frac{1}{1+e^{-{\mathbf{w}}^{\mathsf{T}}{\mathbf{x}}_i}}$ 为 sigmoid 函数, 它将取值范围为 $(-\infty ,+\infty )$ 的 ${\mathbf{w}}^{\mathsf{T}}{\mathbf{x}}_i$ 压缩到了取值范围为 $(0,1)$ 的 $h({\mathbf{x}}_i)$.

• 当 $y_i=0$ (为负例) 时, 优化目标中的 $(1-h({\mathbf{x}}_i))$ 起作用, 即预测值越小, 相应项越大;
• 当 $y_i=1$ (为正例) 时, 优化目标中的 $h({\mathbf{x}}_i)$ 起作用, 即预测值越大, 相应项越大.

3. 方案说明

• 方案和问题定义相同. 这是因为问题定义成这样, 方案也就固定了.
• 使用 sigmoid 函数的原因, 以及极大似然估计的推导, 不包含在本贴中.
• 每个点对优化目标都有贡献 (后面讲到 SVM 会回顾这里). 如果远离分割面而且分类正确, 则相应项接近 1; 如果远离分割面而且分类错误, 则相应项接近 0.
• 极大似然估计, 在机器学习中频繁被用到. 你值得拥有!

4. 方案求解

• 连乘用 $\log$ 变成连加, $\log$ 是一个单调函数, 不影响最大化目标. 这也是常用招数.

5. 与线性回归的联系与区别

联系:

• 都是线性模型, logistic 回归还被称为广义线性模型.
  区别:
• 这个是分类, 要把两个类别的点尽可能分开. 直观上来看, logistic 回归比线性回归靠谱. 不过二分类任务的输出只有两个值, 而线性回归的输出是一个实数值, 后者更难把握.