1130. 叶值的最小代价生成树
- 1、问题描述
- 2、解决方案
- 2.1、动态规划
- 2.1.1、问题分析
- 2.1.2、代码实现
- 2.2、单调栈
1、问题描述
1130. 叶值的最小代价生成树
给你一个正整数数组 arr,考虑所有满足以下条件的二叉树:
- 每个节点都有 0 个或是 2 个子节点。
- 数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。
- 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中,返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。如果一个节点有 0 个子节点,那么该节点为叶节点。
示例 1:
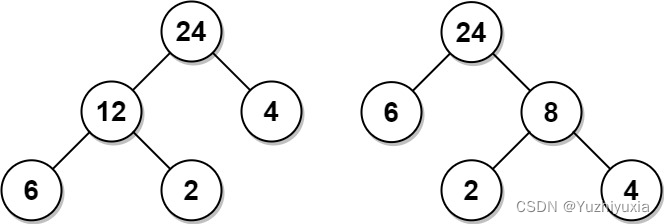
- 输入:arr = [6,2,4]
- 输出:32
- 解释:有两种可能的树,第一种的非叶节点的总和为 36 ,第二种非叶节点的总和为 32 。
示例 2:
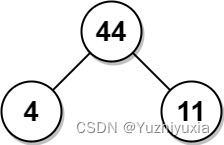
- 输入:arr = [4,11]
- 输出:44
2、解决方案
2.1、动态规划
2.1.1、问题分析
本题本质上就是根据数组arr生成二叉树,然后从所有可能的二叉树中选择代价最小的二叉树,即非叶子节点之和最小的二叉树。由于数组与二叉树中序遍历的叶子节点对应,并且每个节点的子节点个数为0或2,因此问题可以简化为数组arr的拆分问题:对于一个数组,我们可以将它拆分为两部份,分别对应其左右子树,然后递归的对左右子树进行处理,直到剩余1个元素为止。每种拆分方案就对应一种二叉树。
上述的拆分本质就是分治:将大问题拆分为小问题,这里可以采用动态规划算法,对应的转移方程:
假设mk[start][end]表示arr在[start,end]区间内的最大值,则
m
k
[
s
t
a
r
t
]
[
e
n
d
]
=
{
a
r
r
[
s
t
a
r
t
]
,
s
t
a
r
t
=
=
e
n
d
m
a
x
(
a
r
r
[
s
t
a
r
t
]
,
m
k
[
s
t
a
r
t
+
1
]
[
e
n
d
]
)
,
s
t
a
r
t
<
e
n
d
mk[start][end] = \left\{ \begin{matrix} arr[start], start == end \\ max(arr[start], mk[start + 1][end]), start < end \\ \end{matrix} \right.
mk[start][end]={arr[start],start==endmax(arr[start],mk[start+1][end]),start<end
假设dp[start][end]表示数组arr在[start,end]区间内的最小代价,则
d
p
[
s
t
a
r
t
]
[
e
n
d
]
=
{
0
,
s
t
a
r
t
=
=
e
n
d
min
i
∈
[
s
t
a
r
t
,
e
n
d
)
(
d
p
[
s
t
a
r
t
]
[
i
]
+
d
p
[
i
+
1
]
[
e
n
d
]
+
m
k
[
s
t
a
r
t
]
[
i
]
∗
m
k
[
i
+
1
]
[
e
n
d
]
)
,
s
t
a
r
t
<
e
n
d
dp[start][end] = \left\{ \begin{matrix} 0, start == end \\ \min_{i\in \mathcal{[start,end)}}(dp[start][i] + dp[i+1][end] + mk[start][i] * mk[i+1][end]), start < end \\ \end{matrix} \right.
dp[start][end]={0,start==endmini∈[start,end)(dp[start][i]+dp[i+1][end]+mk[start][i]∗mk[i+1][end]),start<end
2.1.2、代码实现
class Solution {
public:
int mctFromLeafValues(vector<int>& arr) {
int length = arr.size();
vector<vector<int>> dp(length, vector<int>(length, INT_MAX));
vector<vector<int>> mk(length, vector<int>(length, 0));
for(int end = 0; end < length; ++end){
dp[end][end] = 0;
mk[end][end] = arr[end];
for(int start = end - 1; start >= 0; --start){
//这里找[start,end]区间内的最大值
mk[start][end] = arr[start] > mk[start + 1][end] ? arr[start] : mk[start + 1][end];
for(int split = start; split < end; ++split){
//计算当前区间[start,end]内以split分割后的代价
int val = dp[start][split] + dp[split + 1][end] + mk[start][split] * mk[split + 1][end];
//当前区间[start,end]内所有分割的最小代价
dp[start][end] = val < dp[start][end] ? val : dp[start][end];
}
}
}
return dp[0][length - 1];
}
};