判断一个点是否在凸多边形内的方法很多，此处仅给出使用向量叉积法判断点是否在凸多边形内的方法。

以下图为例说明问题：

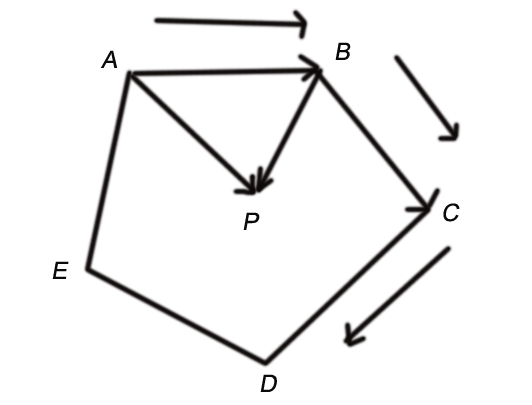
原理：

1. 将多边形的第 i 条边的第一个顶点指向点 P 得到向量 v1，然后将从第一个顶点指向第二个顶点得到向量 v2，叉乘这两个向量。

2. 如果叉乘结果与上一条边的叉乘结果的乘积大于 0 则继续执行；如果乘积小于 0，表示点 P 不在凸多边形内，直接返回即可。

切记：

此种办法只能用来判断凸多边形，且要求凸多边形的点以固定的顺序给出，例如固定为逆时针或顺时针。

C++语言版本的实现，请参考我的这篇博客

如何判断一个点是否在凸多边形内 - C++_YZF_Kevin的博客-CSDN博客

golang语言的实验结果如下图，main函数最后有判断几个点是否在多边形中的举例

 实现的golang代码如下：

package main

import (
   "fmt"
)

type Point struct {
   X float64
   Y float64
}
func (p *Point) GetX() float64 { return p.X }
func (p *Point) GetY() float64 { return p.Y }

// point1和point2的向量
func SubPoint(point1 *Point, point2 *Point) *Point{
   return &Point{
      X: point1.GetX() - point2.GetX(),
      Y: point1.GetY() - point2.GetY(),
   }
}

// 向量积（叉乘）
func CrossProduct(point1 *Point, point2 *Point) float64 {
   return point1.GetX()*point2.GetY() - point2.GetX()*point1.GetY()
}

// 判断一个点是否在多边形内
func IsPointInConvexPolygon(aPoints []*Point, vTarget *Point) bool {
   if len(aPoints) == 0 {
      return false
   }

   var nCurCrossProduct   float64
   var nLastValue           float64

   for i:=0; i<len(aPoints); i++ {
      vU := SubPoint(vTarget, aPoints[i])
      nNextIndex := (i + 1) % len(aPoints)
      vV := SubPoint(aPoints[nNextIndex], aPoints[i])
      nCurCrossProduct = CrossProduct(vU, vV)
      if i>0 && nCurCrossProduct*nLastValue<= 0 {
         return false
      }
      nLastValue = nCurCrossProduct
   }

   return true
}

func main() {
   // 多边形的顶点坐标
   polygon := []*Point{{0, 0}, {0, 1158}, {346, 1345}, {750, 1118}, {750, 0}} 

   bSuc1 := IsPointInConvexPolygon(polygon, &Point{350, 1160})
   fmt.Println("bSuc1=",bSuc1)

   bSuc2 := IsPointInConvexPolygon(polygon, &Point{2, 1190})
   fmt.Println("bSuc2=",bSuc2)

   bSuc3 := IsPointInConvexPolygon(polygon, &Point{749, 1118})
   fmt.Println("bSuc3=",bSuc3)
}