条件随机场模型(Conditional Random Fields, CRF)
条件随机场是给定一组输入随机变量条件下,另一组输出随机变量的条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场。线性链条件随机场,是输入序列对输出序列预测的判别模型,形式为对数线性模型,其学习方法通常是极大似然估计或正则化的极大似然估计。
1、条件随机场模型概念
条件随机场,设X与Y是随机变量,P(Y|X)是在给定X的条件下Y的条件概率分布。若随机变量Y构成一个由无向图G=(V, E)表示的马尔可夫随机场,即:
P
(
Y
v
∣
X
,
Y
w
,
w
≠
v
)
=
P
(
Y
v
∣
X
,
Y
w
,
w
∼
v
)
P(Y_{v}|X,Y_{w}, w≠v)=P(Y_{v}|X,Y_{w}, w\sim v)
P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w∼v)
对任意结点v成立,则称条件概率分布P(Y|X)为条件随机场。式中
w
∼
v
w\sim v
w∼v表示在无向图G=(V, E)中与结点v有边链接的所有结点w,
w
≠
v
w≠v
w=v表示结点v以外的所有结点,
Y
v
,
Y
u
与
Y
w
Y_{v}, Y_{u}与Y_{w}
Yv,Yu与Yw为结点v, u与w对应的随机变量。
2、线性链条件随机场
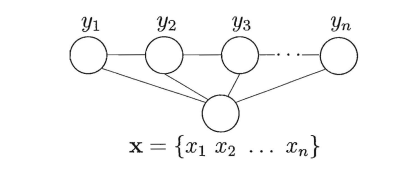
线性链条件随机场,设
X
=
(
X
1
,
X
2
,
.
.
.
,
X
n
)
X=(X_{1},X_{2},...,X_{n})
X=(X1,X2,...,Xn),
Y
=
(
Y
1
,
Y
2
,
.
.
.
,
Y
n
)
Y=(Y_{1},Y_{2},...,Y_{n})
Y=(Y1,Y2,...,Yn)均为线性链表示的随机变量序列,若在给定随机变量序列X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔可夫性
P
(
Y
i
∣
X
,
Y
1
,
.
.
.
,
Y
i
−
1
,
Y
i
+
1
,
.
.
.
,
Y
n
)
=
P
(
Y
i
∣
X
,
Y
i
−
1
,
Y
i
+
1
)
P(Y_{i}|X, Y_{1},...,Y_{i-1}, Y_{i+1}, ..., Y_{n})=P(Y_{i}|X, Y_{i-1}, Y_{i+1})
P(Yi∣X,Y1,...,Yi−1,Yi+1,...,Yn)=P(Yi∣X,Yi−1,Yi+1)
i
=
1
,
2
,
.
.
,
n
(
在
i
=
1
和
n
时只考虑单边)
i=1,2,..,n (在i=1和n 时只考虑单边)
i=1,2,..,n(在i=1和n时只考虑单边)
则称P(Y|X)为线性链条件随机场。在标注问题中,X表示输入观察序列,Y表示对应的输出标记序列或状态序列。
3、马尔可夫随机场
马尔可夫随机场(Markov random field)又称为概率无向图模型(probabilistic undirected graphical model)是一个可以由无向图表示的联合概率分布。
设有联合分布P(Y),由无向图G=(V, E)表示,在图G中,节点表示随机变量,边表示随机变量之间的依赖关系。如果联合概率分布P(Y)满足成对、局部或全局马尔可夫性,就称此联合概率分布为马尔可夫随机场(概率无向图模型)。
其中,Y是一组随机变量,由无向图G=(V, E)表示概率分布P(Y),即在图G中,结点 v ∈ V v\in V v∈V表示一个随机变量 Y v Y_{v} Yv, Y = ( Y v ) v ∈ V Y=(Y_{v})_{v\in V} Y=(Yv)v∈V;边 e ∈ E e\in E e∈E表示随机变量之间的概率依赖关系。
4、马尔可夫性
(一)成对马尔可夫性:设u和v是无向图G中任意两个没有边链接的结点,结点u和v分别对应随机变量
Y
u
Y_{u}
Yu和
Y
v
Y_{v}
Yv。其他所有结点为O,对应的随机变量组是
Y
O
Y_{O}
YO。成对马尔可夫性是指给定随机变量组
Y
O
Y_{O}
YO的条件下随机变量
Y
u
Y_{u}
Yu和
Y
v
Y_{v}
Yv是条件独立的,即
P
(
Y
u
,
Y
v
∣
Y
O
)
=
P
(
Y
u
∣
Y
O
)
P
(
Y
v
∣
Y
O
)
P(Y_{u},Y_{v}| Y_{O}) = P(Y_{u}|Y_{O})P(Y_{v}|Y_{O})
P(Yu,Yv∣YO)=P(Yu∣YO)P(Yv∣YO)
(二)局部马尔可夫性:设
v
∈
V
v\in V
v∈V是无向图G中任意一个结点,W是与v有边连接的所有结点,O是v,W以外的其他所有结点。v表示的随机变量是
Y
v
Y_{v}
Yv,W表示的随机变量组是
Y
W
Y_{W}
YW,O表示的随机变量组是
Y
O
Y_{O}
YO。局部马尔可夫性是指在给定随机变量组
Y
W
Y_{W}
YW的条件下随机变量
Y
v
Y_{v}
Yv与随机变量组
Y
O
Y_{O}
YO是独立的即
P
(
Y
v
,
Y
O
∣
Y
W
)
=
P
(
Y
v
∣
Y
W
)
P
(
Y
O
∣
Y
W
)
P(Y_{v}, Y_{O}| Y_{W}) = P(Y_{v}|Y_{W})P(Y_{O}|Y_{W})
P(Yv,YO∣YW)=P(Yv∣YW)P(YO∣YW)
在
P
(
Y
O
∣
Y
W
)
>
0
P(Y_{O}|Y_{W})>0
P(YO∣YW)>0时,等价地
P
(
Y
v
∣
Y
W
)
=
P
(
Y
v
∣
Y
W
,
Y
O
)
P(Y_{v}|Y_{W}) = P(Y_{v}|Y_{W}, Y_{O})
P(Yv∣YW)=P(Yv∣YW,YO)
(三)全局马尔可夫性:设几点集合A,B是在无向图G中被结点集合C分开的任意结点集合。结点集合A,B和C所对应的随机变量组分别是
Y
A
Y_{A}
YA,
Y
B
Y_{B}
YB和
Y
C
Y_{C}
YC。全局马尔可夫性是指给定随机变量组
Y
C
Y_{C}
YC条件下随机变量组
Y
A
Y_{A}
YA和
Y
B
Y_{B}
YB是条件独立的,即
P
(
Y
A
,
Y
B
∣
Y
C
)
=
P
(
Y
A
∣
Y
C
)
P
(
Y
B
∣
Y
C
)
P(Y_{A}, Y_{B}| Y_{C}) = P(Y_{A}|Y_{C})P(Y_{B}|Y_{C})
P(YA,YB∣YC)=P(YA∣YC)P(YB∣YC)
5、线性链条件随机场整体流程
线性链条件随机场用于标注问题,在条件概率模型P(Y|X)中,Y是输出变量表示标记序列,X是输入变量表示需要标注的观测序列。也把标记序列称为状态序列。
学习时,利用训练数据集通过极大似然估计或正则化的极大似然估计得到条件概率模型
P
^
(
Y
∣
X
)
\hat{P} (Y|X)
P^(Y∣X);
预测时,对于给定的输入序列x,求出条件概率
P
^
(
y
∣
x
)
\hat{P} (y|x)
P^(y∣x)最大的输出序列
y
^
\hat{y}
y^。
Reference
1.《统计学习方法》,李航著
2.《机器学习》,周志华著