来源:力扣(LeetCode)
描述:
给你一个正整数数组 arr,考虑所有满足以下条件的二叉树:
- 每个节点都有 0 个或是 2 个子节点。
- 数组
arr中的值与树的中序遍历中每个叶节点的值一一对应。 - 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中,返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。
如果一个节点有 0 个子节点,那么该节点为叶节点。
示例 1:
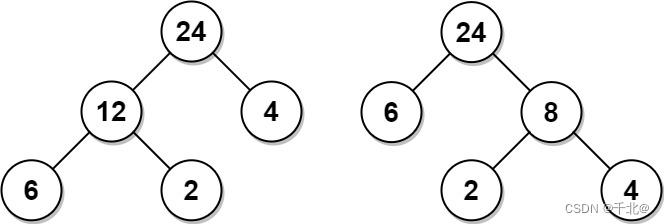
输入:arr = [6,2,4]
输出:32
解释:有两种可能的树,第一种的非叶节点的总和为 36 ,第二种非叶节点的总和为 32 。
示例 2:
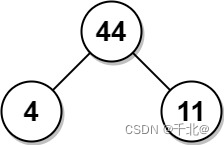
输入:arr = [4,11]
输出:44
提示:
- 2 <= arr.length <= 40
- 1 <= arr[i] <= 15
- 答案保证是一个 32 位带符号整数,即小于 231。
方法一:动态规划
已知数组 arr 与二叉树的中序遍历的所有叶子节点对应,并且二叉树的每个节点都有 0 个节点或 2 个节点。考虑数组 arr 可以生成的所有二叉树,我们可以将 arr 切分成任意两个非空子数组,分别对应左子树和右子树,然后递归地对两个非空子树组执行相同的操作,直到子数组大小等于 1,即叶子节点,那么一种切分方案对应一个合法的二叉树。
使用 dp[i][j] 表示子数组 [i, j] (i ≤ j) 对应的子树所有非叶子节点的最小总和,那么 dp[i][j] 可以通过切分子树求得,状态转移方程如下:

其中 mik 表示子数组 [i,k] 的最大值,可以预先计算并保存下来。
代码:
class Solution {
public:
int mctFromLeafValues(vector<int>& arr) {
int n = arr.size();
vector<vector<int>> dp(n, vector<int>(n, INT_MAX / 4)), mval(n, vector<int>(n));
for (int j = 0; j < n; j++) {
mval[j][j] = arr[j];
dp[j][j] = 0;
for (int i = j - 1; i >= 0; i--) {
mval[i][j] = max(arr[i], mval[i + 1][j]);
for (int k = i; k < j; k++) {
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + mval[i][k] * mval[k + 1][j]);
}
}
}
return dp[0][n - 1];
}
};
执行用时:4 ms, 在所有 C++ 提交中击败了77.21%的用户
内存消耗:9 MB, 在所有 C++ 提交中击败了25.58%的用户
复杂度分析
时间复杂度:O(n3),其中 n 是数组 arr 的长度。三重循环需要 O(n3) 的空间。
空间复杂度:O(n2)。保存 dp 和 mval 需要 O(n2) 的空间。
方法二:单调栈
方法一的思路是自上而下构建二叉树,这里我们可以尝试自下而上构建二叉树:
- 选择 arr 两个相邻的值,即两个节点,将它们作为一个新节点的左子节点和右子节点;
- 将这个新节点在数组 arr 替代这两个节点;
- 如果 arr 剩余的元素数目大于 1,执行步骤 1,否则终止,那么剩余的节点就是构建的二叉树的根节点。
问题可以转化为:给定一个数组 arr,不断地合并相邻的数,合并代价为两个数的乘积,合并之后的数为两个数的最大值,直到数组只剩一个数,求最小合并代价和。
假设一个数 arr[i] (0 < i < n − 1),满足 arr[i−1] ≥ arr[i] 且 arr[i] ≤ arr[i+1],如果 arr[i−1] ≤ arr[i+1],那么优先将 arr[i] 与 arr[i−1] 合并是最优的,反之如果 arr[i−1] > arr[i+1],那么优先将 arr[i] 与 arr[i+1] 合并是最优的。
按照这种思路,套用单调栈算法(栈元素从底到顶是严格递减的),我们遍历数组 arr,记当前遍历的值为 x。
如果栈非空且栈顶元素小于等于 x,那么说明栈顶元素(类似于 arr[i])是符合前面所说的最优合并的条件,将栈顶元素 y 出栈:
- 如果栈空或栈顶元素大于 x,那么将 y 与 x 合并,合并代价为 x × y,合并之后的值为 x;
- 否则将 y 与栈顶元素合并,合并代价为 y 与栈顶元素的乘积,合并之后的值为栈顶元素。
重复以上过程直到栈空或栈顶元素大于 x,然后将 x 入栈。
经过以上合并过程后,栈中的元素从底到顶是严格递减的,因此可以不断地将栈顶的两个元素出栈,合并,再入栈,直到栈元素数目小于 2。返回最终合并代价和即可。
代码:
class Solution {
public:
int mctFromLeafValues(vector<int>& arr) {
int res = 0;
stack<int> stk;
for (int x : arr) {
while (!stk.empty() && stk.top() <= x) {
int y = stk.top();
stk.pop();
if (stk.empty() || stk.top() > x) {
res += y * x;
} else {
res += stk.top() * y;
}
}
stk.push(x);
}
while (stk.size() >= 2) {
int x = stk.top();
stk.pop();
res += stk.top() * x;
}
return res;
}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:8.1 MB, 在所有 C++ 提交中击败了76.28%的用户
复杂度分析
时间复杂度:O(n),其中 n 为数组 arr 的长度。每次循环都有入栈或出栈操作,总次数不超过 2 × n,因此时间复杂度为 O(n)。
空间复杂度:O(n)。栈 stk 需要 O(n) 的空间。
author:LeetCode-Solution