0-1背包和完全背包搞清楚即可。
0-1背包问题-一维
背包有最大重量的限制,物品有重量有价值,那么在最大背包的限制下,能够得到的最大价值是多少?
暴力解法
每个物品都有放和不放两种状态,那么遍历所有的组合就可以得到背包问题的暴力解法。
动态规划
- dp[j]:容量为j的背包所能达到的最大价值
- 递推公式:
dp[j] = max(dp[j],dp[j-weight[i]]+value[j]) - 初始化 dp[0] = 0
- 遍历顺序:第一个for循环遍历物品,第二个遍历背包并且是倒序遍历
- 为什么需要倒序遍历重量:防止一个物品被多次遍历,反过来才能够保证物品不被多次遍历。
- 为什么需要先遍历物品再遍历背包:如果先遍历背包再遍历物品那么会导致dp数组中的所有数值均为同一个数值。
- 打印dp数组
def test_1_wei_bag_problem():
weight = [1, 3, 4]
value = [15, 20, 30]
bag_weight = 4
# 初始化: 全为0
dp = [0] * (bag_weight + 1)
# 先遍历物品, 再遍历背包容量
for i in range(len(weight)):
for j in range(bag_weight, weight[i] - 1, -1):
# 递归公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp)
test_1_wei_bag_problem()
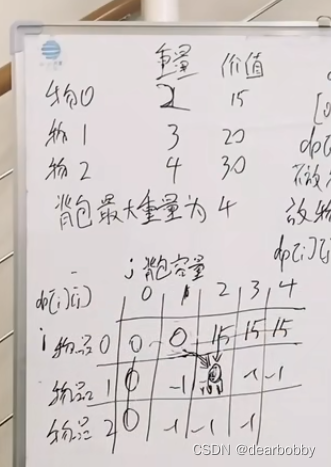
0-1背包问题-二维
- dp数组的含义:dp[i][j]下标为0-i之间的物品,任取放进容量为j的背包里
- 递推公式
不放物品i,j中可以放的最大价值为dp[i-1][j]
放物品i,dp[i-1][j-weight[i]](不放物品i的最大价值)+ value[i]
那么此时的递推公式为:两个部分的值取max
- 遍历顺序
对于二维数组的0-1背包问题遍历两个均可以。先遍历背包和物品都可以。
- dp数组的初始化
def test_2_wei_bag_problem1(bag_size, weight, value) -> int:
rows, cols = len(weight), bag_size + 1
dp = [[0 for _ in range(cols)] for _ in range(rows)]
# 初始化dp数组.
for i in range(rows):
dp[i][0] = 0
first_item_weight, first_item_value = weight[0], value[0]
for j in range(1, cols):
if first_item_weight <= j:
dp[0][j] = first_item_value
# 更新dp数组: 先遍历物品, 再遍历背包.
for i in range(1, len(weight)):
cur_weight, cur_val = weight[i], value[i]
for j in range(1, cols):
if cur_weight > j: # 说明背包装不下当前物品.
dp[i][j] = dp[i - 1][j] # 所以不装当前物品.
else:
# 定义dp数组: dp[i][j] 前i个物品里,放进容量为j的背包,价值总和最大是多少。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)
print(dp)
416. 分割等和子集
本题可以抽象成为0-1背包问题,物品的重量和价值均相等,如果当前重量与背包的重量相同即可得到最终是可以分成两个部分的。
二维数组
dp[i][j] :表示0-i个物体放在重量为j的背包中,所能够获得的最大价值
class Solution:
def canPartition(self, nums: List[int]) -> bool:
if sum(nums) % 2 != 0:
return False
# 二维情况
target = sum(nums)//2
rows, cols = len(nums),sum(nums)//2+1
# 建立背包问题的二维数组
dp = [[0 for _ in range(cols)] for _ in range(rows)]
# 初始化dp数组
for i in range(rows):
dp[i][0] = 0
for j in range(1,cols):
if j >= nums[0]:
dp[0][j] = nums[0]
for i in range(1,rows):
cur_weight = nums[i]
cur_value = nums[i]
for j in range(1,cols):
# 递归公式
if cur_weight > j:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j],dp[i-1][j-cur_weight] + cur_value)
return dp[-1][cols-1] == target
一维数组
dp[j] :表示容量为j的背包所能容纳的最大价值的物品是多少。
将每一个物品分别放入背包中,对背包的容积进行遍历即可。
class Solution:
def canPartition(self, nums: List[int]) -> bool:
# 一维数组的情况
# dp[j]表述容量为j的背包所能达到的最大价值
# 两层for循环不能颠倒
if sum(nums) % 2:
return False
target = sum(nums) // 2
dp = [0] * (target+1)
# 先遍历物品再遍历背包
for i in range(len(nums)):
for j in range(target,nums[i]-1,-1):
dp[j] = max(dp[j], dp[j-nums[i]]+nums[i])
return dp[-1] == target