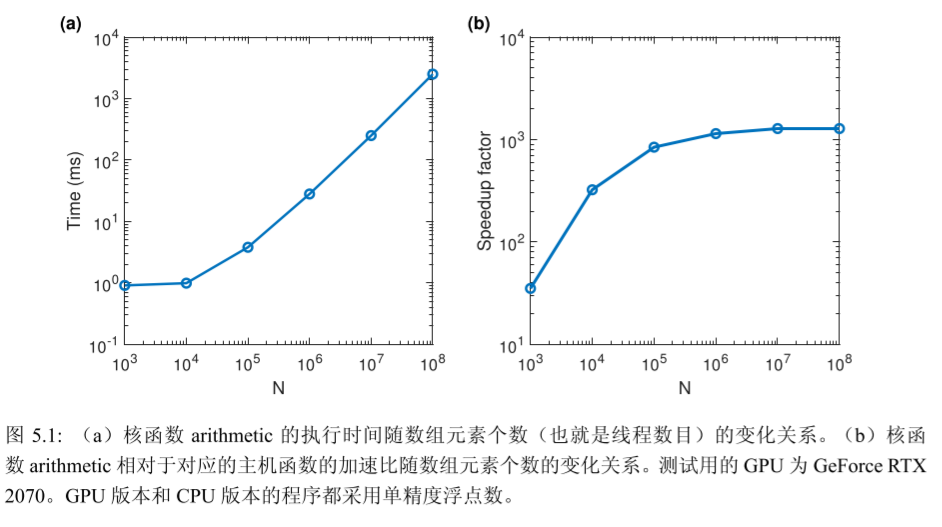
推荐可视化插入、删除节点的二叉树网站:Red/Black Tree Visualization (usfca.edu)
1. 概述
红黑树(Red-Black Tree)是一种自平衡的二叉搜索树(Binary Search Tree)。它在普通二叉搜索树的基础上通过引入额外的颜色属性和一些特定的规则来保持树的平衡,以提供更高效的插入、删除和查找操作。红黑树的时间复杂度也是 O(log N)
2. 特点
-
二叉搜索树特性:红黑树是一棵二叉搜索树,即左子树中的所有节点的值小于当前节点的值,右子树中的所有节点的值大于当前节点的值。
-
节点颜色:每个节点被标记为红色或黑色。
-
根节点和叶子节点:根节点和叶子节点(NIL节点或空节点)都是黑色的。
-
红色节点规则:不能有两个相邻的红色节点,即红色节点的父节点和子节点都不能是红色节点。
-
黑色节点规则:从根节点到叶子节点的任意路径上的黑色节点数量是相同的(黑色节点高度相等)。
-
最长路径和最短路径:红黑树的最长路径不超过最短路径的两倍,保证了树的平衡性。比如:黑黑黑黑黑(5个) 和 红 黑 红 黑 红 黑 红 黑 红 黑(10个)
3. 红黑树与AVL的区别
红黑树(Red-Black Tree)和AVL树都是自平衡的二叉搜索树,它们在保持树的平衡性和提供高效的插入、删除和查找操作方面有相似的目标。然而,它们在实现上有一些区别:
平衡性要求:AVL树要求左右子树的高度差不超过1,而红黑树没有明确的高度差限制,它只要求满足红黑树的五个性质即可。
平衡调整操作:AVL树在插入或删除节点后,可能需要进行更多的旋转操作来保持平衡,以满足高度差限制。而红黑树的平衡调整操作相对较少,通常只需要进行颜色变换和旋转。
维护开销:由于AVL树要求更严格的平衡,它的平衡调整操作相对较多,因此在频繁的插入和删除操作时,AVL树可能需要更多的平衡调整,导致维护开销较大。而红黑树的平衡调整操作相对较少,所以在插入和删除操作频繁的情况下,红黑树通常具有更好的性能。
内存占用:AVL树通常需要额外的平衡因子来记录每个节点的高度差,因此占用的内存空间相对较大。而红黑树只需要一个额外的颜色属性来记录节点的颜色,因此在内存占用上相对更优。
综上所述,AVL树在保持严格的平衡性方面更强,适用于对平衡性要求较高的场景,但在频繁的插入和删除操作下会有较大的维护开销。而红黑树则在平衡性要求相对较宽松的情况下提供较好的性能和较低的维护开销,适用于广泛的应用场景。
4. 红黑树的插入过程
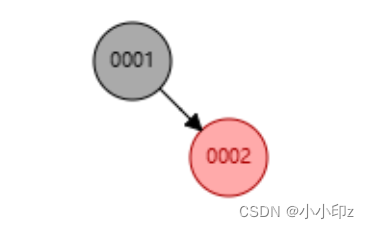
(1)插入 1,2
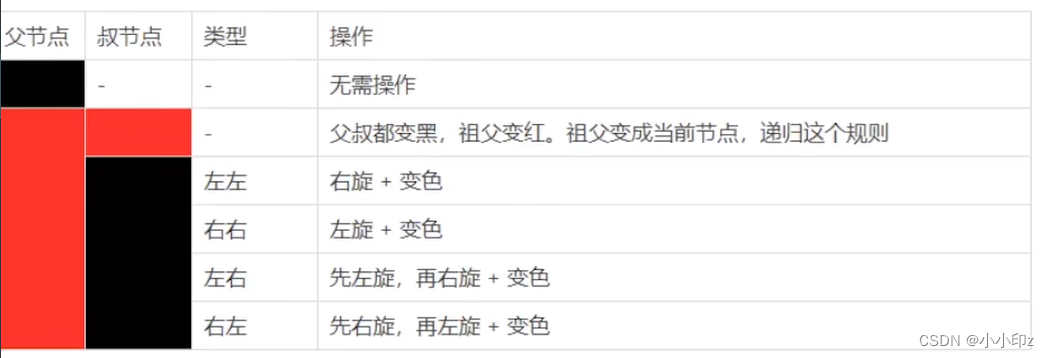
(2)插入 3,父节点是红,叔节点是黑,类型是右右(RR),需要左旋+变色
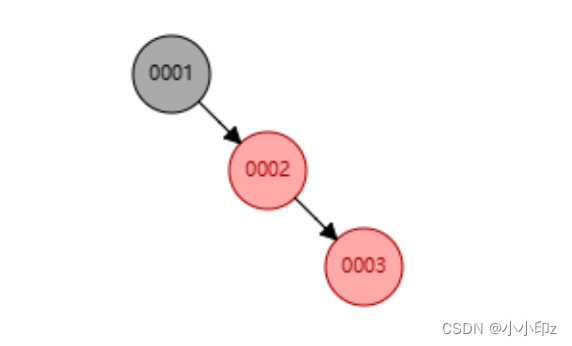
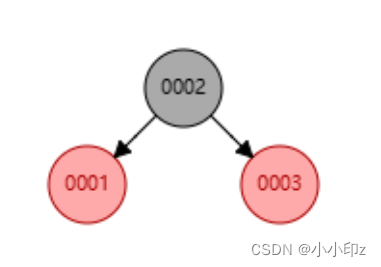
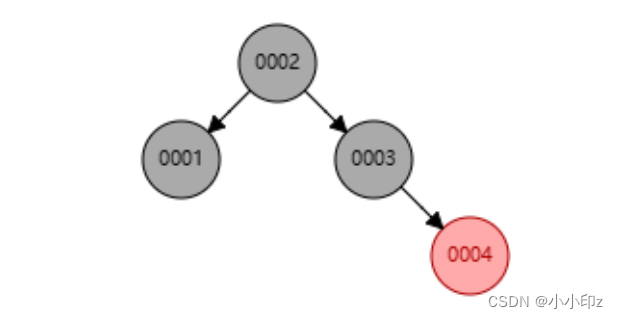
(3) 插入 4,父节点是红,叔节点也是红
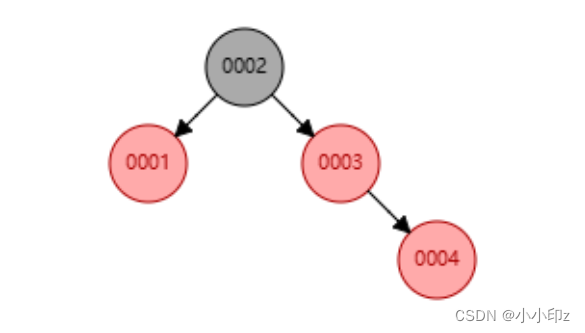
父节点和叔节点都变黑,祖父变红,祖父变成当前节点,也就是2节点变为当前节点,递归这个规则:(2节点为根节点,变黑)
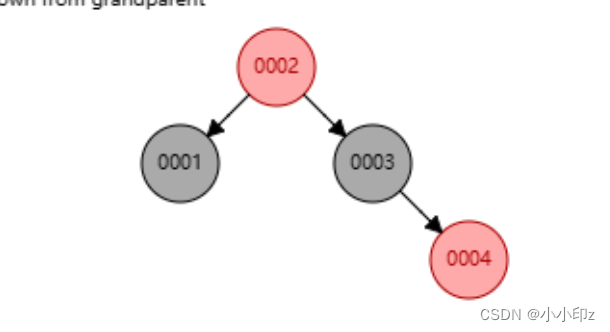
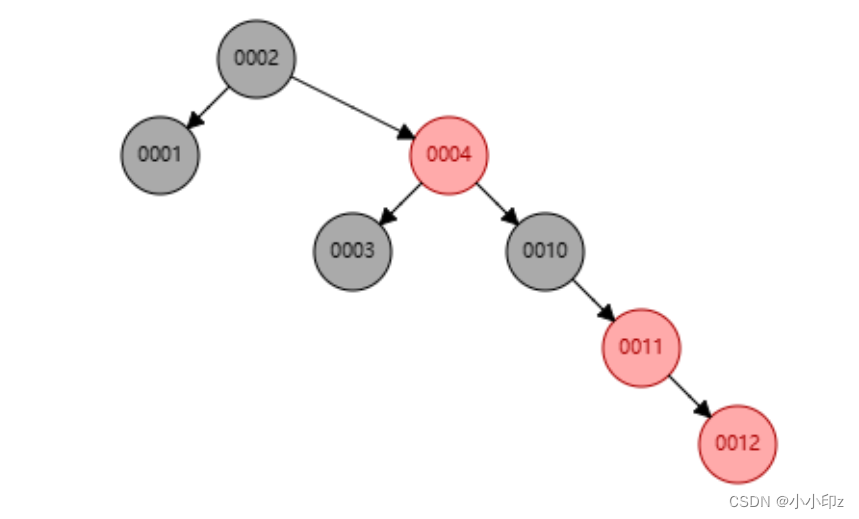
(4) 插入 10,12

(5)插入 11,父节点是红,叔节点是黑,类型是右左(RL),需要先右旋,再左旋+变色

右旋
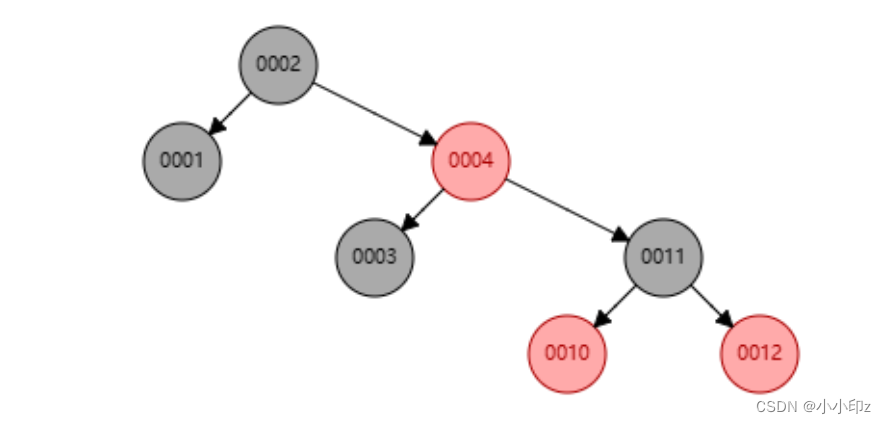
左旋

变色
5. 面试问题
Java8中,HashMap实现,每一个桶是一个链表,当链表长度大于阈值(默认为 8),会将链表转换成红黑树,为什么选择转换为红黑树,而不是BST和AVL?
答:
不用BST:递增或递减序列可能会退化成链表
不同AVL:AVL的平衡条件更为严格,需要更频繁的进行旋转操作,会导致性能下降。
另外,红黑树相对于AVL树在插入和删除操作时的平衡调整次数较少,这也意味着在频繁进行插入和删除操作时,红黑树的性能可能会更好。
因此,在HashMap中选择使用红黑树作为链表长度超过阈值时的数据结构转换,是为了在平衡性和性能之间取得一个较好的平衡。这样可以在大多数情况下保持良好的性能,并避免由于频繁的旋转操作而引起的性能下降。