数据结构与算法07：高效的排序算法

news2024/11/30 2:44:47

目录

归并排序

快速排序

桶排序

计数排序

基数排序

对比各类排序算法

每日一练：排序链表

在上一篇文章中分析了简单的三种排序算法：冒泡排序、插入排序、选择排序，这三种排序算法的时间复杂度都是O(n^2)，效率不是很高。如果要对大规模的数据排序，可以考虑使用归并排序和快速排序，可以实现O(nlogn)的时间复杂度。

归并排序

归并排序使用的是“分而治之”的思想，就是把一个无序的数组从中间分成前后两部分，然后对这两个部分再次分割，一直分割到最小单元（每个子数组只包含一个元素），然后对每一个最小单元分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。整个实现过程可以使用递归的方式，如下图所示：

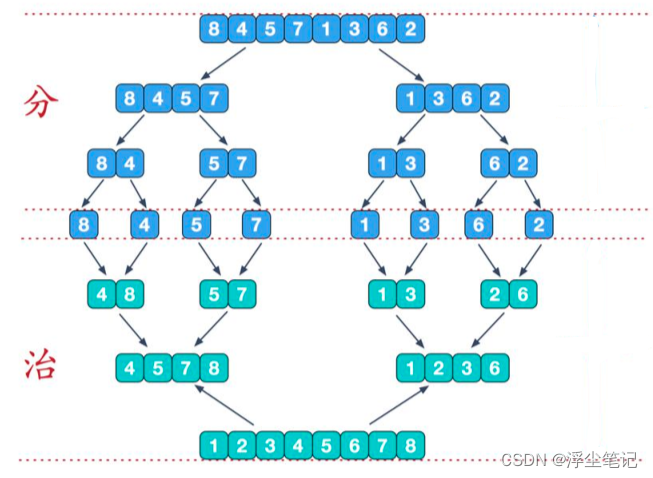
归并排序动画图

既然可以用递归代码来实现归并排序，那么首先就得分析得出递推公式，然后找到终止条件，最后将递推公式转换成递归代码。下面是实现过程的伪代码思路：

// 归并排序算法, A 是数组，n 表示数组大小
merge_sort(A, n) {
  merge_sort_c(A, 0, n-1)
}
 
// 递归调用函数
merge_sort_c(A, p, r) {
  // 递归终止条件
  if p >= r  then return

  // 取 p 到 r 之间的中间位置 q
  q = (p+r) / 2

  // 分治递归
  merge_sort_c(A, p, q)
  merge_sort_c(A, q+1, r)

  // 将 A[p...q] 和 A[q+1...r] 合并为 A[p...r]
  merge(A[p...r], A[p...q], A[q+1...r])
}

转换成Go语言代码如下：

// go-algo-demo/sort1/MergeSort.go

func MergeSort(arr []int) {
	arrLen := len(arr)
	if arrLen <= 1 {
		return
	}

	mergeSort(arr, 0, arrLen-1)
}

//分
func mergeSort(arr []int, start, end int) {
	if start >= end {
		return
	}

	mid := (start + end) / 2
	mergeSort(arr, start, mid)
	mergeSort(arr, mid+1, end)
	merge(arr, start, mid, end)
}
//合
func merge(arr []int, start, mid, end int) {
	tmpArr := make([]int, end-start+1)

	i := start
	j := mid + 1
	k := 0
	for ; i <= mid && j <= end; k++ {
		if arr[i] < arr[j] {
			tmpArr[k] = arr[i]
			i++
		} else {
			tmpArr[k] = arr[j]
			j++
		}
	}

	for ; i <= mid; i++ {
		tmpArr[k] = arr[i]
		k++
	}
	for ; j <= end; j++ {
		tmpArr[k] = arr[j]
		k++
	}
	copy(arr[start:end+1], tmpArr)
}

func main() {
	arr := []int{8, 4, 5, 7, 1, 3, 6, 2}
	MergeSort(arr)
	fmt.Println(arr) //[1 2 3 4 5 6 7 8]
}

归并排序的性能分析：

  • 在merge()合并的函数中，可以保证相同的元素在合并前后保持顺序不变，因此是一个稳定的排序算法。
  • 在合并两个有序数组为一个有序数组时需要开辟额外的存储空间，空间复杂度是O(n)，所以归并排序不是原地排序算法。
  • 时间复杂度比较稳定，在最好情况、最坏情况、平均情况下的时间复杂度都是 O(nlogn)。

【问】为什么归并排序的时间复杂度是O(nlogn)？

【答】因为归并排序首先使用了二分的思想，这个过程的时间复杂度是O(logn)，然后再进行有序子数组合并的时候，需要O(n)的时间复杂度，因此整个过程就是O(n * logn)。

快速排序

快速排序也简称为“快排”，也是使用了分治思想，把原始的数组筛选分成较小和较大的两个子数组，然后递归的排序两个子数组。首先在数组中选择任意一个数据作为分区点（设为Q），然后遍历整个数组，将小于Q的部分(0到Q)放到左边，大于Q的部分(Q+1到结尾)放到右边，Q在中间。然后使用递归分别处理这三部分的数据，直到区间缩小为1。这个过程基本就是一个二叉树的前序遍历的过程。看下图所示：

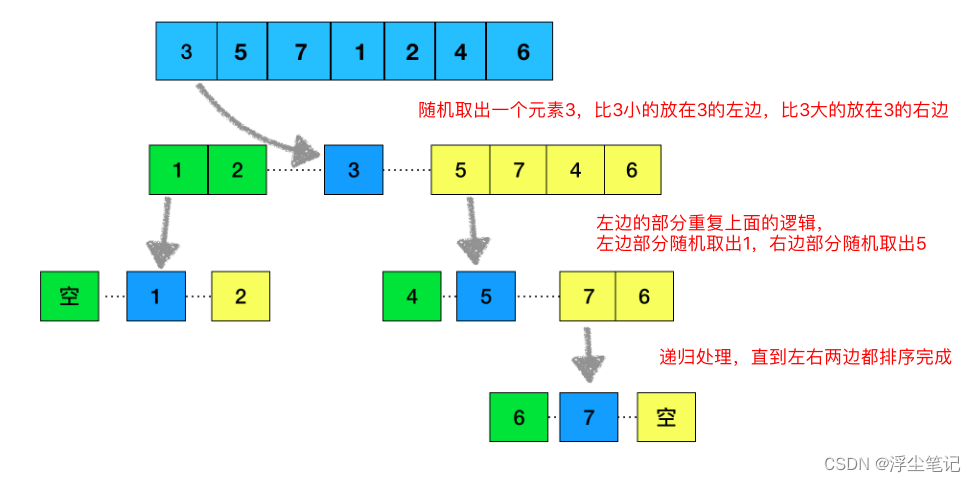
快速排序动画图

递推公式的伪代码：

// 快速排序，A 是数组，n 表示数组的大小
quick_sort(A, n) {
  quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数，p,r 为下标
quick_sort_c(A, p, r) {
  if p >= r then return
  
  q = partition(A, p, r) // 获取分区点
  quick_sort_c(A, p, q-1)
  quick_sort_c(A, q+1, r)
}

转换成Go语言代码如下： 

// go-algo-demo/sort1/QuickSort.go
func QuickSort(arr []int) {
	arrLen := len(arr)
	if arrLen <= 1 {
		return
	}
	quickSort(arr, 0, arrLen-1)
}

func quickSort(arr []int, start, end int) {
	if start >= end {
		return
	}
	Q := partition(arr, start, end)
	quickSort(arr, start, Q)
	quickSort(arr, Q+1, end)
}

func partition(arr []int, low, high int) int {
	Q := arr[low]
	for low < high {
		//指针从右边开始向右找到一个比Q小的数
		for low < high && arr[high] > Q {
			high--
		}
		//将这个数放到low位，注意第一次这个位置放的是Q值，所以不会丢
		arr[low] = arr[high]
		//指针从左边开始向右找到第一个比Q大的数
		for low < high && arr[low] < Q {
			low++
		}
		//将这个数赋值给之前的high指针，因为之前high指针指向的数已经被一定，所以不会丢
		arr[high] = arr[low]
	}
	//最后将Q的值放入合适位置，此时low与high相等
	arr[low] = Q
	return low
}

func main() {
	arr := []int{8, 4, 5, 7, 1, 3, 6, 2}
	QuickSort(arr)
	fmt.Println(arr) //[1 2 3 4 5 6 7 8]
}

快速排序的性能分析：

  • 快排在分区的过程中涉及到元素的交换，所以快排是不稳定的排序算法。
  • 快排通过原地分区函数，可以实现原地排序，空间复杂度O(1)。
  • 快排如果每次选中的Q都是中位数，那么时间复杂度就是 O(nlogn)；如果每次选中的Q都是最小值或最大值，那么此时最坏情况下的时间复杂度是O(n^2)，这种概率不大；快排的平均时间复杂度是O(nlogn)。

对比归并排序和快速排序：

  • 归并排序的处理过程是由下到上的，先处理子问题，然后再合并；快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。
  • 归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法；快速排序通过原地分区函数，可以实现原地排序，占用内存较少。

如何优化快速排序？

上面分析了，快排的时间复杂度如果成为O(n^2)的主要原因分区点选的不够合理，最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。一般可以使用 三数取中法 来获取分区点：从数组区间的头部、尾部、中间 分别取出一个数，然后对比大小，然后使用这3个数的中间值作为分区点。如果要排序的数组比较大，那么也可能需要 “五数取中” 或者 “十数取中”。 

桶排序

上面说的归并排序和快速排序的时间复杂度都是O(nlogn)，还有以下三种时间复杂度是O(n)的排序算法：桶排序、计数排序、基数排序，这三种排序算法时线性排序的，不涉及元素之间的比较操作。

桶排序：将要排序的数据按照一定的规则分到几个有序的桶里，每个桶里的数据再单独排序，桶内排完序之后再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。如下图所示：

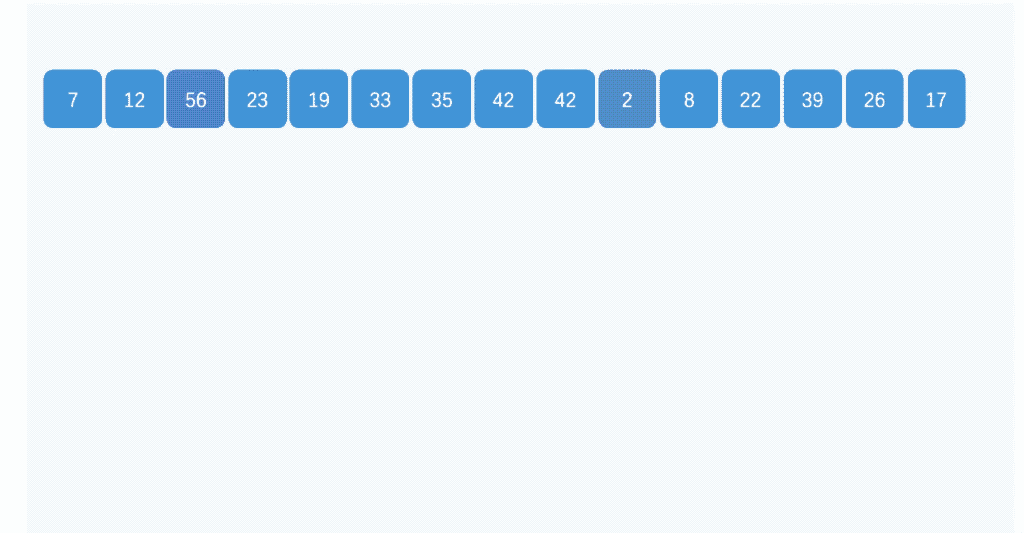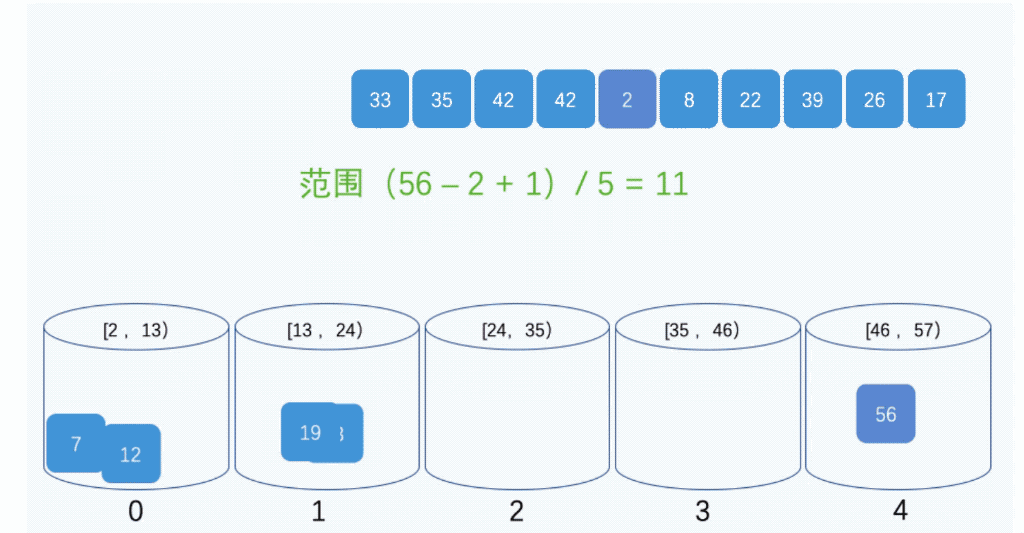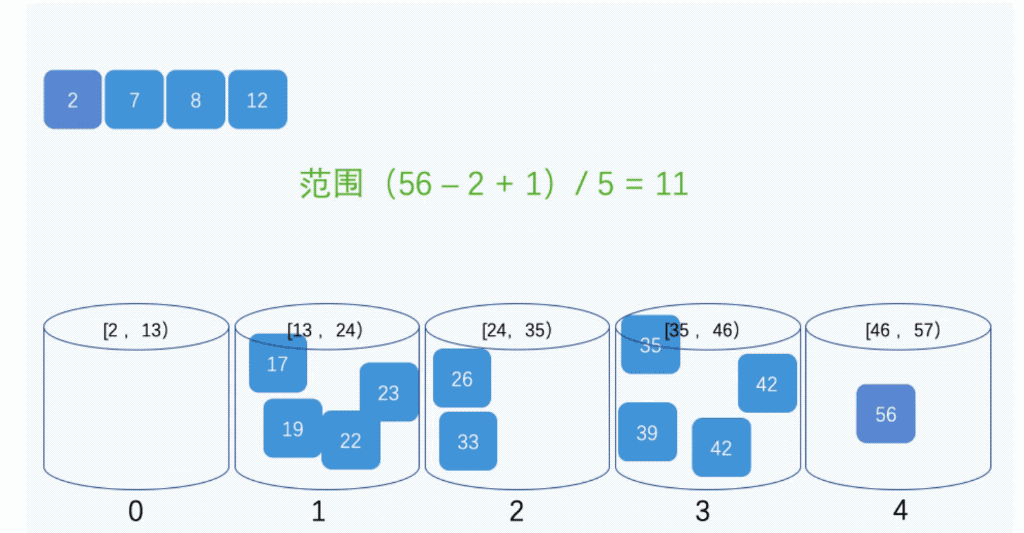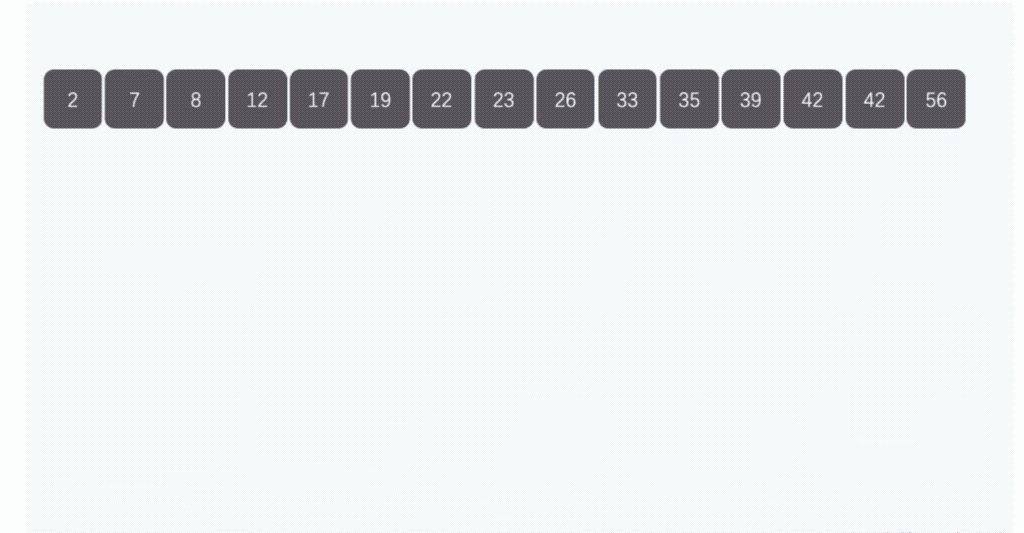
桶排序需要注意以下几个问题：

  • 所有的桶需要是有序的，这样就不需要再对桶进行排序；
  • 数据在各个桶之间的分布应该是比较均匀的，才能保证达到O(n)的时间复杂度；
  • 桶排序比较适合用在以下场景：数据量比较大、内存有限、无法将数据全部加载到内存中；

假设现在有10GB的订单数据，希望按订单金额排序，但是计算机的内存只有几百 MB，没办法一次性把10GB的数据都加载到内存中，就可以使用桶排序，方法如下：

先把所有的订单根据金额划分到100个有序的桶里面，第1个桶存储1-1000元的数据，第2个桶存储1001-2000元的数据，以此类推，第100个桶存储99000-100000元的数据。如果订单金额分布比较均匀，那么每个桶中大约存储100MB的数据，就可以针对每个桶使用快速排序或者归并排序；如果订单金额分布不均匀，比如1-1000元之间的比较多，那么就对这个桶里面的数据继续拆分为多个桶来处理。

计数排序

计数排序其实是桶排序的一种特殊情况，当要排序的数据所处的范围区间并不大（比如最大值是 k，就可以把数据划分成 k 个桶），每个桶内的数据值都是相同的，省掉了桶内排序的时间。

还是类似上面的例子，只不过场景改成了10GB的用户信息，希望按照用户年龄排序，用户的年龄范围是0-120岁，就可以把这些数据划分到121个有序的桶中，每个桶内都是相同的数据，所以最终只需要依次扫描每个桶内的数据就实现了最终的排序。

计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下转化为非负整数。

基数排序

基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则基数排序的时间复杂度就无法做到 O(n) 了。

假设要对 10万 个手机号码从小到大排序，就可以使用基数排序，方法如下：如果两个手机号码前两位已经比较出大小了，就没必要再比较后面的数字了。

对比各类排序算法

  • 对数据规模比较小的数据进行排序，可以选择时间复杂度为O(n^2)的排序算法，比如：冒泡、插入、选择；
  • 对数据规模比较大的数据进行排序，可以选择时间复杂度为O(nlogn)的排序算法，比如：快排、归并；
  • 归并排序不是原地排序算法，空间复杂度为O(n)，对空间资源消耗会很多，假设原数组100MB，使用归并排序就要消耗200MB的空间资源。
  • 快速排序在平均时间复杂度为O(nlogn)，最坏的时间复杂度也有可能退化为O(n^2)，但是一般概率不大。
排序算法时间复杂度是否稳定排序是否原地排序
冒泡排序O(n^2)是是
插入排序O(n^2)是是
选择排序O(n^2)否是
快速排序O(nlogn)否是
归并排序O(nlogn)是否
计数排序O(n+k)，k是数据范围是否
桶排序O(n)是否
基数排序O(n)是否

源代码：https://gitee.com/rxbook/go-algo-demo/tree/master/sort1

每日一练：排序链表

力扣21. 合并两个有序链表

力扣148. 排序链表 

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：输入：head = [4,2,1,3]，输出：[1,2,3,4]
示例 2：输入：head = [-1,5,3,4,0]，输出：[-1,0,3,4,5]

思路：使用归并排序，找到中间的元素然后拆分数组进行排序，最后再合并。时间复杂度O(nlogn)，空间复杂度O(n)。

//https://gitee.com/rxbook/go-algo-demo/blob/master/leetcode/SortList.go

package main

import "fmt"

type ListNode struct {
	Val  int
	Next *ListNode
}

// 递归到只有一个数字的时候返回，然后再合并
func sortList(head *ListNode) *ListNode {
	if head == nil || head.Next == nil {
		return head
	}
	mid := findMiddle(head)

	tail := mid.Next
	mid.Next = nil

	left := sortList(head)
	right := sortList(tail)

	return mergeTwoLists(left, right)
}

// 快慢指针找链表的中点
func findMiddle(head *ListNode) *ListNode {
	slow := head
	fast := head.Next
	for fast != nil && fast.Next != nil {
		slow = slow.Next
		fast = fast.Next.Next
	}
	return slow
}

// 力扣21.合并两个有序链表
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
	dummy := new(ListNode)
	cur := dummy
	// 遍历两个链表，每次比较链表头的大小，每次让较小值添加到 dummy 的后面，并且让较小值所在的链表后移一位
	for {
		if l1 == nil && l2 == nil {
			break
		}
		if l1 == nil {
			cur.Next = l2
			break
		}
		if l2 == nil {
			cur.Next = l1
			break
		}
		// 会出现一条链表遍历完，另外一条链表没遍历完的情况，需要将没遍历的链表添加到结果链表中
		if l1.Val < l2.Val {
			cur.Next = l1
			l1 = l1.Next
			cur = cur.Next
		} else {
			cur.Next = l2
			l2 = l2.Next
			cur = cur.Next
		}
	}
	return dummy.Next
}

func main() {
	list := &ListNode{
		Val: -1, Next: &ListNode{
			Val: 5, Next: &ListNode{
				Val: 3, Next: &ListNode{
					Val: 4, Next: &ListNode{
						Val: 0,
					},
				},
			},
		},
	}
	list.Print()           //-1->5->3->4->0
	sortList(list).Print() //-1->0->3->4->5
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/589700.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

KUC711AE101 3BHB004661R0101 用于精确误差仿真的设备

KUC711AE101 3BHB004661R0101 用于精确误差仿真的设备

KUC711AE101 3BHB004661R0101 最近推出的欧姆龙自动化产品包括CJ2H-CPU可编程自动化控制器、NS15超清晰15英寸HMI以及用于CJ和CS平台的基于PLC的高速位置控制器模块。通过以太网/IP使用CJ2H-CPU的行业标准、基于标记的编程有助于缩短程序开发时间和故障排除。CX-One有助于满足市…
阅读更多...
分布式时序数据库DolphinDB

分布式时序数据库DolphinDB

简介 DolphinDB不仅可作为分布式数据仓库或者内存数据库来使用&#xff0c;而且自带丰富的计算工具&#xff0c;可作为一个研究工具或研究平台来使用。DolphinDB对时间序列数据的处理特别友好&#xff0c;非常适合量化金融、物联网等领域的海量数据分析。例如在量化金融领域的交…
阅读更多...
JavaEE进阶（5/29）Mybatis

JavaEE进阶（5/29）Mybatis

目录 1.什么是Mybatis 2.Mybatis组成部分 3.配置Mybatis中的存放路径 4.设置路径 6.yml配置MyBatis的xml配置文件路径 1.什么是Mybatis 它是一款持久层框架&#xff0c;支持自定义SQL&#xff0c;存储过程&#xff08;一个方法&#xff0c;封装了一堆SQL&#xff08;包括判断/变…
阅读更多...
spring security实现authorization code模式，自定义登录页面，自动授权，自定义密码编码，跳转登录页面http转https

spring security实现authorization code模式，自定义登录页面，自动授权，自定义密码编码，跳转登录页面http转https

spring security实现authorization code模式# 系列文章目录 SpringSecurity实现OAuth2 JWT和OAuth2在SpringBoot下的实现 spring security实现authorization code模式 摘要自定义登录页面自动授权自定义密码验证跳转登录页面http转https 摘要 为了将老项目接口安全暴露给第三…
阅读更多...
在线帮助中心搭建利器：Baklib

在线帮助中心搭建利器：Baklib

帮助中心是一个提供服务和支持的虚拟平台&#xff0c;旨在为客户提供解决问题和获取信息的途径。它通常包含企业或组织的产品或服务的相关信息、解决方案、操作指南和常见问题等信息。通过帮助中心&#xff0c;用户可以自助查询并解决问题&#xff0c;从而提高了客户的满意度和…
阅读更多...
Neutron — 虚拟机网卡创建过程

Neutron — 虚拟机网卡创建过程

目录 文章目录 目录创建并绑定虚拟机的虚拟网卡1、创建 VM 和 Port 记录2、创建 VM 和 Port 实体3、更新 Port 状态 创建并绑定虚拟机的虚拟网卡 在 OpenStack 中&#xff0c;Nova 负责虚拟机的生命周期管理&#xff0c;Neutron 负责虚拟网络的生命周期管理。而虚拟机的虚拟网…
阅读更多...
两个直线/线段的交点 - C++

两个直线/线段的交点 - C++

问题&#xff0c;求上图中线段AB 和线段CD的交点P的坐标 根据《算法艺术与信息学竞赛》&#xff0c;公式如下 原理&#xff1a; 利用叉积求得点P分线段DC的比&#xff0c;然后利用高中学习的定比分点坐标公式求得分点P的坐标 c代码如下 #include <math.h> #include &l…
阅读更多...
压力山大？搭建JMeter分布式压测环境轻松应对！

压力山大？搭建JMeter分布式压测环境轻松应对！

目录 引言 windows环境部署 1.安装环境变量 2.配置环境变量 3.修改Jmeter配置文件 4.启动jmeter 5.启动分布式服务 Linux环境部署 1.安装JDKJmeter 2.环境优化 4.编写Jmeter脚本 5.启动Jmeter 6.停止Jmeter 7.打包查看测试报告 引言 您想要提高您的应用程序的性…
阅读更多...
【JavaSE】Java基础语法(三十五)：多线程实战

【JavaSE】Java基础语法(三十五)：多线程实战

文章目录 1. 多线程入门1.1 多线程相关概念1.2 什么是多线程1.3 多线程的创建方式1.3.1 继承 Thread 的方式1.3.2 实现 Runnable 接口的方式1.3.3 实现 Callable 接口的方式1.3.4 Thread 类中常用方法1.3.5 sleep() 方法 和 wait() 方法区别&#xff1a; 2. 线程安全2.1 线程安…
阅读更多...
破坏单例模式--存在的问题---问题的解决

破坏单例模式--存在的问题---问题的解决

目录 破坏单例模式--存在的问题---问题的解决 问题演示 破坏单例模式&#xff1a; 序列化 反射 序列化反序列化&#xff1a; 代码&#xff1a; 运行结果&#xff1a; 反射 代码&#xff1a; 运行结果&#xff1a; 问题的解决 序列化、反序列方式破坏单例模式的解…
阅读更多...
Elasticsearch 8.X 性能优化参考 —— 筑梦之路

Elasticsearch 8.X 性能优化参考 —— 筑梦之路

Elasticsearch 是实现用户无缝搜索体验的关键工具。它通过提供快速、准确和相关的搜索结果&#xff0c;彻底改变了用户与应用程序的互动方式。然而&#xff0c;要确保 Elasticsearch 部署达到最佳性能&#xff0c;就必须关注关键指标&#xff0c;并对诸如索引、缓存、查询、搜索…
阅读更多...
monorepo 项目 Unable to resolve path to module ‘xxx‘.eslintimport/no-unresolved

monorepo 项目 Unable to resolve path to module ‘xxx‘.eslintimport/no-unresolved

同事问了一个问题&#xff0c;他现在参加了一个项目&#xff0c;这个项目是个monorepo 项目。 也就是多包管理、前后端一起都是js 写的。 问题 后端express 项目里配置的路径别名&#xff0c;eslint 不认识&#xff0c;报错。 Unable to resolve path to module /app/Prisma.e…
阅读更多...
Phaser笔记-鼠标点击获取坐标键盘控制sprite

Phaser笔记-鼠标点击获取坐标键盘控制sprite

代码如下&#xff1a; import phaser;class PlayGame extends Phaser.Scene {constructor() {super("PlayGame");}preload() {this.load.spritesheet(run, assets/_Run.png, {frameWidth: 120, frameHeight: 80});this.load.spritesheet(idle, assets/_Idle.png, {f…
阅读更多...
GEE：对Sentinel-2遥感影像进行处理，水体提取与可视化

GEE：对Sentinel-2遥感影像进行处理，水体提取与可视化

作者&#xff1a;CSDN _养乐多_ 本文介绍了通过Google Earth Engine平台&#xff0c;并使用哨兵数据提取水体掩膜的方法和代码。通过裁剪和去除云等处理步骤&#xff0c;最终得到具有水体掩膜的影像&#xff0c;并进行可视化和导出。这种方法基于归一化水体指数&#xff08;N…
阅读更多...
MIT 6.S081 (BOOK-RISCV-REV1)教材第一章内容

MIT 6.S081 (BOOK-RISCV-REV1)教材第一章内容

MIT 6.S081 教材第一章内容 引言第一章 操作系统接口进程和内存I/O和文件描述符管道文件系统真实世界 引言 MIT 6.S081 2020 操作系统 本文为MIT 6.S081课程第一章教材内容翻译加整理。 本课程前置知识主要涉及: C语言(建议阅读C程序语言设计—第二版)RISK-V汇编推荐阅读: 程…
阅读更多...
JavaScript 数据透视表 DHTMLX Pivot Crack

JavaScript 数据透视表 DHTMLX Pivot Crack

DHTMLX Pivot JavaScript 数据透视表 - 强大的数据汇总和报告 使用我们的高速 JavaScript/HTML5 Pivot 组件可视化您的复杂数据&#xff0c;从而提高您的商业智能。 它可以帮助您以方便的方式汇总大型数据集。 主要特征 纯 JavaScript 库&#xff0c;可轻松与任何服务器端集成…
阅读更多...
Linux安装Mysql8，过程详细（离线安装mysql）

Linux安装Mysql8，过程详细（离线安装mysql）

因公司需要&#xff0c;需要在服务器上安装一个mysql&#xff0c;但是机器没有外网权限&#xff0c;所以记录一下安装过程&#xff0c;供大家参考。 官网下载安装包 地址&#xff1a;https://dev.mysql.com/downloads/ 如图示&#xff0c;选择MySQL Community Server 如图示&a…
阅读更多...
git新手将网页设计代码提交到github上

git新手将网页设计代码提交到github上

以下是将代码提交到Github上的一些步骤。如果中途遇到问题或不会的需要我帮忙&#xff0c;可以文章底部联系我。 1. 创建Github账户 首先&#xff0c;您需要在Github上注册一个账户。 如果您已经有账户了&#xff0c;请跳过这一步。 2. 创建一个新的repository 在您的Githu…
阅读更多...
格式化数字的实用命令：numfmt

格式化数字的实用命令：numfmt

在 Linux 系统中&#xff0c;numfmt 是一个用于格式化数字的实用工具。它可以将数字转换为不同的表示方式&#xff0c;如十进制、二进制、字节单位等。本文将详细介绍 numfmt 命令的使用方法&#xff0c;并提供一些适合初学者的示例。 Numfmt 命令语法 numfmt 命令的基本语法如…
阅读更多...
搭建stm32电机控制代码框架（四）——单路PWM生成

搭建stm32电机控制代码框架（四）——单路PWM生成

STM32中单路PWM的生成一般是基于某一个通用定时器&#xff0c;本次小实验选取TIM2通用定时器&#xff0c;选择PA5作为PWM端口输出。配置步骤如下&#xff1a; 第一步&#xff1a;配置外部晶振与基本的时钟&#xff0c;如下图所示。 &#xff08;1&#xff09;选择外部晶振 &a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023